Determinante Eigenschaften. Verringern der Ordnung der Determinante

Etwas Nummer, nach einer bestimmten Regel berechnet und genannt bestimmend.

Die Notwendigkeit, das Konzept einzuführen bestimmend - die Zahlen charakterisierend Quadrat Bestellmatrix n , ist eng verwandt mit der Lösung von Systemen linearer algebraischer Gleichungen.

Determinante einer Matrix EIN wir werden bezeichnen: | EIN| oder d.

Die Determinante einer Matrix erster OrdnungEIN = (ein 11) heißt ein Element ein elf . Zum Beispiel für EIN= (-4) wir haben | EIN| = -4.

Die Determinante einer Matrix zweiter Ordnung namens Nummer bestimmt durch die Formel

|EIN| = .

Zum Beispiel | EIN| = .

In Worten kann diese Regel wie folgt geschrieben werden: Mit Ihrem eigenen Vorzeichen müssen Sie das Produkt der verbundenen Elemente nehmen Hauptdiagonale, und die Produkte von Elementen, die durch die Eckpunkte von Dreiecken verbunden sind, für die Basis parallel zur Hauptdiagonalen... Beim umgekehrten Vorzeichen nehmen wir ähnliche Produkte, nur in Bezug auf die Seitendiagonale.

Zum Beispiel,

Bestimmung der Determinante einer Matrix n Wir geben nicht die te Reihenfolge an, sondern zeigen nur die Methode, um sie zu finden.

Außerdem statt Worte Determinante einer Matrix n-te Ordnung Lass uns einfach sagen bestimmend n-te Ordnung... Lassen Sie uns neue Konzepte vorstellen.

Gegeben eine quadratische Matrix n te Bestellung.

Unerheblichm ij-Element ein ij Matrizen EIN namens bestimmend (n-1) te Ordnung aus der Matrix EIN löschen ich-te Zeile und J te Spalte.

Das algebraische Komplement A ij des Elements a ij der Matrix A ist dessen Minor, genommen mit dem Vorzeichen (-1) i + j:

EIN ij = (-1) i + j m ich,

jene. ein algebraisches Komplement fällt entweder mit seinem Minor zusammen, wenn die Summe der Zeilen- und Spaltenzahlen eine gerade Zahl ist, oder unterscheidet sich von ihm im Vorzeichen, wenn die Summe der Zeilen- und Spaltenzahlen eine ungerade Zahl ist.

Zum Beispiel für Elemente ein 11 und ein 12 Matrizen A = Minderjährige

m 11 = EIN 11 = ,

m 12 = ,

ein EIN 12 = (-1) 1+2 m 12 = -8.

Satz (über die Entwicklung der Determinante) . Die Determinante einer quadratischen Matrix ist gleich der Summe der Produkte der Elemente einer beliebigen Zeile (Spalte) durch ihre algebraischen Komplemente, d.h.

|EIN| = ein i1 EIN i1 + ein i2 EIN i2 + ... + ein in EIN in,
für jeden ich = 1, 2, …, n

|EIN| = ein 1j EIN 1j + ein 2j EIN 2j + ... + ein NJ EIN NJ,

für jeden J = 1, 2, …, n

Die erste Formel heißt ich-te Zeile, und das zweite ist Zerlegung der Determinante in Elemente J te Spalte.

Es ist leicht zu verstehen, dass mit Hilfe dieser Formeln jede Determinante n-te Ordnung kann auf die Summe der Determinanten reduziert werden, deren Ordnung 1 weniger ist usw. bis wir Determinanten 3. oder 2. Ordnung erreichen, deren Berechnung nicht mehr schwierig ist.

Um die Determinante zu finden, können die folgenden grundlegenden Eigenschaften angewendet werden:

1. Wenn eine Zeile (oder Spalte) der Determinante aus Nullen besteht, dann ist die Determinante selbst gleich Null.

2. Beim Vertauschen von zwei beliebigen Zeilen (oder zwei Spalten) wird die Determinante mit -1 multipliziert.

3. Determinante mit zwei identischen oder proportionalen Zeilen (oder Spalten) ist gleich Null.

4. Der gemeinsame Faktor der Elemente einer beliebigen Zeile (oder Spalte) kann aus dem Vorzeichen der Determinante entnommen werden.

5. Der Wert der Determinante ändert sich nicht, wenn alle Zeilen und Spalten vertauscht werden.

6. Der Wert der Determinante ändert sich nicht, wenn eine weitere Zeile (Spalte) multipliziert mit einer beliebigen Zahl zu einer der Zeilen (oder zu einer der Spalten) hinzugefügt wird.

7. Die Summe der Produkte von Elementen einer beliebigen Zeile (oder Spalte) einer Matrix durch die algebraischen Komplemente von Elementen einer anderen Zeile (Spalte) dieser Matrix ist gleich Null.

8. Die Determinante des Produkts zweier quadratischer Matrizen ist gleich dem Produkt ihrer Determinanten.

Die Einführung des Konzepts einer Determinante einer Matrix ermöglicht es uns, eine weitere Aktion mit Matrizen zu definieren - das Finden der inversen Matrix.

Für jede Zahl ungleich Null gibt es eine inverse Zahl, so dass das Produkt dieser Zahlen eins ergibt. Auch für quadratische Matrizen gibt es ein solches Konzept.

Matrix EIN-1 heißt umkehren in Richtung Quadrat Matrix EIN wenn diese Matrix mit der sowohl rechts als auch links gegebenen multipliziert wird, ergibt Identitätsmatrix, d.h.

EIN× EIN -1 = EIN-1 × EIN= E.

Aus der Definition folgt, dass nur eine quadratische Matrix eine Inverse hat; in diesem Fall ist die inverse Matrix ebenfalls ein Quadrat derselben Ordnung. Allerdings hat nicht jede quadratische Matrix ihre eigene Inverse.

ALGEBRAISCHE ERGÄNZUNGEN UND MINDERJÄHRIGE

Wir haben eine Determinante dritter Ordnung: .

Unerheblich entspricht diesem Element ein ij Determinante dritter Ordnung, wird als Determinante zweiter Ordnung bezeichnet, die aus dem Gegebenen durch Streichen der Zeile und Spalte gewonnen wird, an deren Schnittpunkt das gegebene Element steht, d.h. ich-te Zeile und J te Spalte. Minor entsprechend einem gegebenen Element ein ij wird bezeichnen M ij.

Zum Beispiel, unerheblich M12 entsprechend dem Element ein 12, es wird eine Determinante geben 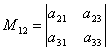, die durch Löschen der 1. Zeile und 2. Spalte aus der gegebenen Determinante erhalten wird.

Somit zeigt die Formel, die die Determinante dritter Ordnung definiert, dass diese Determinante gleich der Summe der Produkte der Elemente der 1. Reihe durch die entsprechenden Minderjährigen ist; in diesem Fall das dem Element entsprechende Moll ein 12, mit einem „-“-Zeichen, d.h. das können wir schreiben

Ebenso können wir Definitionen von Minor für Determinanten zweiter und höherer Ordnung einführen.

Lassen Sie uns ein weiteres Konzept vorstellen.

Algebraisches Komplement Element ein ij die Determinante heißt ihr Minor M ij multipliziert mit (–1) i + j.

Algebraisches Komplement eines Elements ein ij bezeichnet Ein ij.

Aus der Definition ergibt sich, dass der Zusammenhang zwischen dem algebraischen Komplement eines Elements und seinem Nebenelement durch die Gleichheit ausgedrückt wird Ein ij= (–1) i + j M ij.

Zum Beispiel,

Beispiel. Eine Determinante ist gegeben. Finden A 13, A 21, A 32.

Es ist leicht zu sehen, dass Formel (1) mit den algebraischen Komplementen von Elementen in der Form geschrieben werden kann:

Ähnlich wie bei dieser Formel können Sie die Determinante in die Elemente einer beliebigen Zeile oder Spalte zerlegen.

Zum Beispiel kann die Faktorisierung der Determinante durch die Elemente der 2. Zeile wie folgt erhalten werden. Nach Eigenschaft 2 der Determinante gilt:

Erweitern wir die erhaltene Determinante um die Elemente der 1. Reihe.

.

(2)

Von hier schon seit die Determinanten zweiter Ordnung in Formel (2) sind die Nebenelemente der Elemente eine 21, eine 22, eine 23... Somit, d.h. erhalten wir die Zerlegung der Determinante in die Elemente der 2. Reihe.

Auf ähnliche Weise können Sie die Faktorisierung der Determinante in Bezug auf die Elemente der dritten Zeile erhalten. Anhand der Eigenschaft 1 von Determinanten (über Transposition) kann man zeigen, dass ähnliche Erweiterungen auch für die Erweiterung nach Spaltenelementen gelten.

Somit ist der folgende Satz wahr.

Satz (über die Entwicklung einer Determinante in einer gegebenen Zeile oder Spalte). Die Determinante ist gleich der Summe der Produkte der Elemente einer ihrer Zeilen (oder Spalten) durch ihre algebraischen Komplemente.

All dies gilt auch für Determinanten höherer Ordnung.

Beispiele.

INVERSE MATRIX

Das Konzept einer inversen Matrix wird nur für . eingeführt quadratische Matrizen.

Wenn EIN Ist eine quadratische Matrix, dann umkehren dafür wird eine Matrix als Matrix bezeichnet, bezeichnet mit A -1 und die Bedingung erfüllen. (Diese Definition wird analog zur Multiplikation von Zahlen eingeführt)

EIGENSCHAFT 1. Der Wert der Determinante ändert sich nicht, wenn alle ihre Zeilen durch Spalten ersetzt werden und jede Zeile durch eine Spalte mit derselben Nummer ersetzt wird, d. h.

EIGENSCHAFT 2. Die Permutation von zwei Spalten oder zwei Zeilen einer Determinante entspricht der Multiplikation mit -1. Zum Beispiel,

.

EIGENSCHAFT 3. Wenn die Determinante zwei identische Spalten oder zwei identische Zeilen hat, ist sie gleich Null.

EIGENSCHAFT 4. Die Multiplikation aller Elemente einer Spalte oder einer Zeile der Determinante mit einer beliebigen Zahl k entspricht der Multiplikation der Determinante mit dieser Zahl k. Zum Beispiel,

.

EIGENSCHAFT 5. Wenn alle Elemente einer Spalte oder einer Reihe gleich Null sind, dann ist die Determinante selbst gleich Null. Diese Eigenschaft ist ein Spezialfall der vorherigen (für k = 0).

EIGENSCHAFT 6. Wenn die entsprechenden Elemente zweier Spalten oder zweier Zeilen einer Determinante proportional sind, dann ist die Determinante Null.

EIGENSCHAFT 7. Wenn jedes Element der n-ten Spalte oder n-ten Zeile der Determinante die Summe zweier Terme ist, dann kann die Determinante als Summe zweier Determinanten dargestellt werden, von denen eine in der n-ten Spalte oder , bzw. in der n-ten Reihe hat den ersten von den genannten Begriffen und den anderen - den zweiten; die Elemente an den übrigen Stellen sind für die Meilensteine ​​der drei Determinanten gleich. Zum Beispiel,

EIGENSCHAFT 8. Wenn wir zu den Elementen einer Spalte (oder einer Reihe) die entsprechenden Elemente einer anderen Spalte (oder einer anderen Reihe) addieren, multipliziert mit einem gemeinsamen Faktor, dann ändert sich der Wert der Determinante nicht. Zum Beispiel,

.

Weitere Eigenschaften von Determinanten hängen mit dem Konzept eines algebraischen Komplements und eines Molls zusammen. Der Minor eines bestimmten Elements ist eine Determinante, die sich aus einem gegebenen ergibt, indem eine Zeile und eine Spalte gelöscht werden, an deren Schnittpunkt sich dieses Element befindet.

Das algebraische Komplement eines Elements der Determinante ist gleich dem Minor dieses Elements mit seinem eigenen Vorzeichen, wenn die Summe der Zahlen der Zeile und Spalte, an deren Schnittpunkt sich das Element befindet, eine gerade Zahl ist, und mit dem umgekehrten Vorzeichen, wenn diese Zahl ungerade ist.

Das algebraische Komplement eines Elements bezeichnen wir mit einem Großbuchstaben gleichen Namens und derselben Zahl wie der Buchstabe, der das Element selbst bezeichnet.

EIGENSCHAFT 9. Determinante

gleich der Summe der Produkte der Elemente einer beliebigen Spalte (oder Zeile) durch ihre algebraischen Komplemente.

Mit anderen Worten, es gelten die folgenden Gleichheiten:

, ,

, .

6) Nebensächliche und algebraische Ergänzungen.

Definition. Das Nebenelement der Determinante ist th Auftrag werden genannt bestimmend- te Ordnung, die sich aus dem Gegebenen ergibt bestimmend indem Sie die -te Zeile und die -te Spalte durchstreichen, an deren Schnittpunkt das Element steht.

Bezeichnung:.

Definition. Das algebraische Komplement eines Elements der Ordnungsdeterminante wird als Minor bezeichnet, mit einem Pluszeichen, wenn es eine gerade Zahl ist, und ansonsten mit einem Minuszeichen.

Bezeichnung:.

Satz. (Über die Erweiterung der Determinante.)

Die Determinante ist gleich der Summe der Produkte der Elemente einer beliebigen Zeile (oder einer beliebigen Spalte) der Determinante durch ihre algebraischen Komplemente:

7) Inverse Matrix- eine solche Matrix EIN −1 , wenn mit welcher multipliziert, die ursprüngliche Matrix EIN ergibt sich Identitätsmatrix E:

Quadratische Matrix ist genau dann reversibel, wenn sie nicht entartet ist, d. h bestimmend ist nicht null. Für nicht-quadratische Matrizen und entartete Matrizen es gibt keine inversen Matrizen. Es ist jedoch möglich, dieses Konzept zu verallgemeinern und einzuführen pseudoinverse Matrizen, ähnlich der Umkehrung in vielen Eigenschaften.

8)Matrixrang- die höchste der Bestellungen Minderjährige dieser Matrix ungleich null

Normalerweise wird der Rang einer Matrix mit () oder bezeichnet. Beide Bezeichnungen kamen aus den Fremdsprachen zu uns, daher können beide verwendet werden.

Eigenschaften

Satz (über das grundlegende Moll): Sei r = rang A M das grundlegende Moll der Matrix A, dann:

Basiszeilen und Basisspalten sind linear unabhängig;

jede Zeile (Spalte) der Matrix A ist eine Linearkombination von Grundzeilen (Spalten).

- Befreie die Meise zum sicheren Tod!
Lass die Freiheit sie streicheln!
Und das Schiff segelt und der Reaktor brüllt ...
- Pash, bist du am Arsch?

Ich erinnere mich, dass ich vor der 8. Klasse Algebra nicht mochte. Mir hat es gar nicht gefallen. Sie hat mich angepisst. Weil ich da nichts verstanden habe.

Und dann änderte sich alles, denn ich ging ein Stück durch:

In der Mathematik im Allgemeinen (und der Algebra im Besonderen) baut alles auf einem kompetenten und konsistenten Definitionssystem auf. Sie kennen die Definitionen, Sie verstehen ihre Essenz - es wird nicht schwer sein, den Rest herauszufinden.

So ist es auch mit dem Thema der heutigen Lektion. Wir werden einige verwandte Fragen und Definitionen im Detail betrachten, dank derer Sie sich ein für alle Mal mit Matrizen und Determinanten mit all ihren Eigenschaften befassen werden.

Determinanten sind ein zentrales Konzept der Matrixalgebra. Wie die abgekürzten Multiplikationsformeln werden sie dich während deines fortgeschrittenen Mathematikkurses verfolgen. Deshalb lesen, sehen und verstehen wir gründlich. :)

Und wir beginnen mit dem Intimsten – und was ist eine Matrix? Und wie man richtig damit arbeitet.

Richtige Anordnung der Indizes in der Matrix

Eine Matrix ist nur eine mit Zahlen gefüllte Tabelle. Neo hat damit nichts zu tun.

Eines der wichtigsten Merkmale einer Matrix ist ihre Dimension, d.h. die Anzahl der Zeilen und Spalten, aus denen es besteht. Normalerweise sagen sie, dass eine Matrix $ A $ die Größe $ \ left [m \ mal n \ right] $ hat, wenn sie $ m $ Zeilen und $ n $ Spalten hat. Sie schreiben es so:

Oder so:

Es gibt andere Bezeichnungen - alles hängt von den Vorlieben des Dozenten / Seminaristen / Autors des Lehrbuchs ab. Aber auf jeden Fall tritt bei all diesen $ \ left [m \ mal n \ right] $ und $ ((a) _ (ij)) $ das gleiche Problem auf:

Welcher Index ist für was zuständig? Zuerst kommt die Zeilennummer, dann die Spalte? Oder umgekehrt?

Beim Lesen von Vorlesungen und Lehrbüchern wird die Antwort offensichtlich sein. Aber wenn man bei der Prüfung nur ein Merkblatt mit einem Problem vor sich hat, kann man überfordert und plötzlich verwirrt werden.

Befassen wir uns also ein für alle Mal mit diesem Thema. Erinnern wir uns zunächst an das übliche Koordinatensystem aus dem Schulmathematikkurs:

Einführung eines Koordinatensystems auf einer Ebene

Erinnere dich an sie? Es hat den Ursprung (Punkt $ O = \ left (0; 0 \ right) $) Achsen $ x $ und $ y $, und jeder Punkt auf der Ebene ist eindeutig durch Koordinaten bestimmt: $ A = \ left (1; 2 \ rechts) $, $ B = \ links (3; 1 \ rechts) $ usw.

Nehmen wir nun diese Konstruktion und platzieren sie neben der Matrix, sodass der Ursprung in der oberen linken Ecke liegt. Warum dort? Denn wenn wir ein Buch öffnen, beginnen wir genau ab der linken oberen Ecke der Seite zu lesen – es ist leichter zu merken.

Aber wohin sollen die Achsen gerichtet sein? Wir richten sie so aus, dass unsere gesamte virtuelle "Seite" von diesen Achsen abgedeckt wird. Stimmt, dafür musst du unser Koordinatensystem drehen. Die einzig mögliche Option für eine solche Anordnung:

Nun hat jede Zelle der Matrix einwertige Koordinaten $ x $ und $ y $. Zum Beispiel bedeutet der Datensatz $ ((a) _ (24)) $, dass wir uns auf das Element mit den Koordinaten $ x = 2 $ und $ y = 4 $ beziehen. Auch die Dimensionen der Matrix werden durch ein Zahlenpaar eindeutig festgelegt:

Schauen Sie sich dieses Bild einfach genau an. Spielen Sie mit Koordinaten herum (insbesondere wenn Sie mit echten Matrizen und Determinanten arbeiten) - und Sie werden sehr bald feststellen, dass Sie selbst in den komplexesten Sätzen und Definitionen perfekt verstehen, worum es geht.

Verstanden? Kommen wir zum ersten Schritt der Erleuchtung - der geometrischen Definition der Determinante. :)

Geometrische Definition

Zunächst möchte ich anmerken, dass die Determinante nur für quadratische Matrizen der Form $ \ left [n \ mal n \ right] $ existiert. Eine Determinante ist eine Zahl, die nach bestimmten Regeln berechnet wird und eines der Merkmale dieser Matrix ist (es gibt noch andere Merkmale: Rang, Eigenvektoren, aber dazu in anderen Lektionen).

Was also ist diese Eigenschaft? Was bedeutet es? Es ist einfach:

Die Determinante der quadratischen Matrix $ A = \ links [n \ mal n \ rechts] $ ist das Volumen des $ n $ -dimensionalen Parallelepipeds, das sich bildet, wenn wir die Zeilen der Matrix als die Kanten dieser bildenden Vektoren betrachten parallelepiped.

Die Determinante einer 2x2-Matrix ist beispielsweise nur die Fläche eines Parallelogramms, bei einer 3x3-Matrix jedoch bereits das Volumen eines 3-dimensionalen Parallelepipeds – dasjenige, das im Stereometrieunterricht alle Gymnasiasten wütend macht.

Auf den ersten Blick mag diese Definition völlig unzureichend erscheinen. Aber lassen Sie uns keine voreiligen Schlüsse ziehen - schauen wir uns Beispiele an. Tatsächlich ist alles elementar, Watson:

Aufgabe. Finden Sie die Determinanten der Matrizen:

\ [\ links | \ begin (Matrix) 1 & 0 \\ 0 & 3 \\\ Ende (Matrix) \ right | \ quad \ left | \ begin (Matrix) 1 & -1 \\ 2 & 2 \\\ Ende (Matrix) \ right | \ quad \ left | \ begin (Matrix) 2 & 0 & 0 \\ 1 & 3 & 0 \\ 1 & 1 & 4 \\\ Ende (Matrix) \ right | \]

Lösung. Die ersten beiden Qualifier sind 2x2. Dies sind also nur die Bereiche von Parallelogrammen. Lassen Sie uns sie zeichnen und die Fläche berechnen.

Das erste Parallelogramm baut auf den Vektoren $ ((v) _ (1)) = \ left (1; 0 \ right) $ und $ ((v) _ (2)) = \ left (0; 3 \ right) $:

Die Determinante 2x2 ist die Fläche des Parallelogramms

Offensichtlich ist dies nicht nur ein Parallelogramm, sondern ein ziemliches Rechteck. Sein Gebiet ist

Das zweite Parallelogramm ist aufgebaut auf den Vektoren $ ((v) _ (1)) = \ left (1; -1 \ right) $ und $ ((v) _ (2)) = \ left (2; 2 \ right ) $. Na so was? Dies ist auch ein Rechteck:

Eine weitere Determinante 2x2

Die Seiten dieses Rechtecks ​​(eigentlich die Längen der Vektoren) werden leicht mit dem Satz des Pythagoras berechnet:

\ [\ beginnen (ausrichten) & \ links | ((v) _ (1)) \ rechts | = \ sqrt (((1) ^ (2)) + ((\ links (-1 \ rechts)) ^ (2))) = \ sqrt (2); \\ & \ links | ((v) _ (2)) \ rechts | = \ sqrt (((2) ^ (2)) + ((2) ^ (2))) = \ sqrt (8) = 2 \ sqrt (2); \\ & S = \ links | ((v) _ (1)) \ rechts | \ cdot \ links | ((v) _ (2)) \ rechts | = \ sqrt (2) \ cdot 2 \ sqrt (2) = 4. \\\ Ende (ausrichten) \]

Es bleibt noch die letzte Determinante zu behandeln - es gibt bereits eine 3x3-Matrix. Wir müssen uns an die Stereometrie erinnern:

Die Determinante 3x3 ist das Volumen des Parallelepipeds

Es sieht kopflastig aus, aber tatsächlich reicht es aus, sich die Formel für das Volumen eines Parallelepipeds zu erinnern:

wobei $ S $ die Fläche der Basis ist (in unserem Fall ist dies die Fläche des Parallelogramms auf der Ebene $ OXY $), $ h $ ist die Höhe, die zu dieser Basis gezogen wird (tatsächlich ist die $ z $ -Koordinate des Vektors $ ((v) _ (3) ) $).

Die Fläche eines Parallelogramms (wir haben es separat gezeichnet) ist auch einfach zu berechnen:

\ [\ begin (ausrichten) & S = 2 \ cdot 3 = 6; \\ & V = S \ cdot h = 6 \ cdot 4 = 24. \\\ Ende (ausrichten) \]

Das ist alles! Wir schreiben die Antworten auf.

Antwort: 3; 4; 24.

Eine kurze Anmerkung zum Notationssystem. Jemandem wird es wahrscheinlich nicht gefallen, dass ich die "Pfeile" über den Vektoren ignoriere. Angeblich kann man auf diese Weise einen Vektor mit einem Punkt oder etwas anderem verwechseln.

Aber seien wir ernst: Sie und ich sind bereits erwachsene Jungen und Mädchen, also verstehen wir aus dem Kontext perfekt, wenn es um einen Vektor geht, und wann zu einem Punkt. Pfeile übersät die Geschichte, die bereits mit mathematischen Formeln vollgestopft ist.

Und weiter. Im Prinzip hindert uns nichts daran, die Determinante der 1x1-Matrix zu berücksichtigen - eine solche Matrix ist nur eine Zelle, und die in diese Zelle geschriebene Zahl ist die Determinante. Aber hier gibt es einen wichtigen Hinweis:

Im Gegensatz zum klassischen Volumen gibt uns die Determinante die sogenannte „ orientiertes Volumen", d.h. Volumen unter Berücksichtigung der Reihenfolge der Berücksichtigung von Zeilenvektoren.

Und wenn Sie die Lautstärke im klassischen Sinne des Wortes erhalten möchten, müssen Sie das Determinantenmodul belegen, aber jetzt sollten Sie sich keine Sorgen machen - jedenfalls lernen wir in wenigen Sekunden, jede Determinante mit jedem Vorzeichen zu zählen , Größen usw. :)

Algebraische Definition

Bei aller Schönheit und Klarheit des geometrischen Ansatzes hat er jedoch einen gravierenden Nachteil: Er sagt uns nichts darüber, wie genau diese Determinante zu berechnen ist.

Daher werden wir jetzt eine alternative Definition analysieren - algebraisch. Dazu brauchen wir eine kurze theoretische Vorbereitung, aber am Ende erhalten wir ein Werkzeug, mit dem wir alles in Matrizen zählen können und wie wir wollen.

Es stimmt, dort wird ein neues Problem auftauchen ... aber das Wichtigste zuerst.

Permutationen und Inversionen

Schreiben wir die Zahlen von 1 bis $ n $ in eine Zeile. Am Ende hast du so etwas:

Jetzt (rein zum Spaß) tauschen wir ein paar Zahlen aus. Sie können die nebenstehenden ändern:

Oder Sie können - nicht besonders benachbart:

Und weisst du was? Aber nichts! In der Algebra wird dieser Mist als Permutation bezeichnet. Und es hat eine Menge Eigenschaften.

Definition. Permutation der Länge $ n $ ist eine Zeichenkette von $ n $ verschiedenen Zahlen, die in beliebiger Reihenfolge geschrieben werden. Normalerweise werden die ersten natürlichen Zahlen $ n $ betrachtet (dh nur die Zahlen 1, 2, ..., $ n $), und dann werden sie gemischt, um die gewünschte Permutation zu erhalten.

Permutationen werden wie Vektoren bezeichnet - nur ein Buchstabe und eine sequentielle Auflistung ihrer Elemente in Klammern. Zum Beispiel: $ p = \ left (1; 3; 2 \ right) $ oder $ p = \ left (2; 5; 1; 4; 3 \ right) $. Der Buchstabe kann alles sein, aber lassen Sie es $ p $ sein. :) :)

Außerdem werden wir der Einfachheit halber mit Permutationen der Länge 5 arbeiten - sie sind bereits schwerwiegend genug, um verdächtige Effekte zu beobachten, aber noch nicht so schwerwiegend für ein unreifes Gehirn wie Permutationen der Länge 6 oder mehr. Hier sind Beispiele für solche Permutationen:

\ [\ begin (ausrichten) & ((p) _ (1)) = \ links (1; 2; 3; 4; 5 \ rechts) \\ & ((p) _ (2)) = \ links (1 ; 3; 2; 5; 4 \ rechts) \\ & ((p) _ (3)) = \ links (5; 4; 3; 2; 1 \ rechts) \\\ end (ausrichten) \]

Natürlich kann eine Permutation der Länge $ n $ als Funktion betrachtet werden, die auf der Menge $ \ left \ (1; 2; ...; n \ right \) $ definiert ist und diese Menge bijektiv auf sich selbst abbildet. Kehren wir zu den gerade geschriebenen Permutationen von $ ((p) _ (1)) $, $ ((p) _ (2)) $ und $ ((p) _ (3)) $ zurück, können wir ganz legal schreiben:

\ [((p) _ (1)) \ links (1 \ rechts) = 1; ((p) _ (2)) \ links (3 \ rechts) = 2; ((p) _ (3)) \ links (2 \ rechts) = 4; \]

Die Anzahl der verschiedenen Permutationen der Länge $ n $ ist immer beschränkt und gleich $ n! $ - das ist eine leicht beweisbare Tatsache aus der Kombinatorik. Wenn wir zum Beispiel alle Permutationen der Länge 5 ausschreiben wollen, dann zögern wir, da solche Permutationen

Eines der Schlüsselmerkmale jeder Permutation ist die Anzahl der Inversionen darin.

Definition. Inversion in Permutation $ p = \ left (((a) _ (1)); ((a) _ (2)); ...; ((a) _ (n)) \ right) $ - beliebiges Paar $ \ left (((a) _ (i)); ((a) _ (j)) \ right) $ mit $ i \ lt j $, aber $ ((a) _ (i)) \ gt ( ( a) _ (j)) $. Einfach ausgedrückt liegt eine Inversion vor, wenn eine größere Zahl links von einer kleineren steht (nicht unbedingt der benachbarten).

Wir werden mit $ N \ left (p \ right) $ die Anzahl der Inversionen in der Permutation $ p $ bezeichnen, aber seien Sie bereit, andere Bezeichnungen in verschiedenen Lehrbüchern und verschiedenen Autoren zu treffen - hier gibt es keine einheitlichen Standards. Das Thema Inversionen ist ziemlich umfangreich, und ihm wird eine eigene Lektion gewidmet. Unsere Aufgabe ist es jetzt einfach zu lernen, wie man sie in realen Problemen zählt.

Zählen wir zum Beispiel die Anzahl der Inversionen in der Permutation $ p = \ left (1; 4; 5; 3; 2 \ right) $:

\ [\ left (4; 3 \ right); \ left (4; 2 \ right); \ left (5; 3 \ right); \ left (5; 2 \ right); \ left (3; 2 \ right ).\]

Also $ N \ links (p \ rechts) = 5 $. Wie Sie sehen, ist daran nichts auszusetzen. Lassen Sie es mich gleich sagen: Weiter interessiert uns weniger die Zahl $ N \ left (p \ right) $ als ihre Evenness / Oddness. Und hier kommen wir glatt zum Schlüsselbegriff der heutigen Lektion.

Was ist eine Determinante?

Gegeben sei eine quadratische Matrix $ A = \ left [n \ mal n \ right] $. Dann:

Definition. Die Determinante der Matrix $ A = \ left [n \ mal n \ right] $ ist die algebraische Summe von $ n! $ Termen, die sich wie folgt zusammensetzen. Jeder Term ist das Produkt von $ n $ Matrixelementen, eines aus jeder Zeile und jeder Spalte, multipliziert mit (−1) hoch der Anzahl der Inversionen:

\ [\ links | A \ rechts | = \ Summe \ Grenzen_ (n{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}

Der grundlegende Punkt bei der Auswahl der Faktoren für jeden Term in der Determinante ist die Tatsache, dass sich keine zwei Faktoren in derselben Zeile oder in derselben Spalte befinden.

Aus diesem Grund können wir ohne Einschränkung der Allgemeinheit annehmen, dass die Indizes $ i $ der Faktoren $ ((a) _ (i; j)) $ die Werte 1, ..., $ n $ . "durchlaufen". , und die Indizes $ j $ sind eine Permutation von first:

Und wenn es eine Permutation $ p $ gibt, können wir leicht die Inversionen von $ N \ left (p \ right) $ berechnen - und der nächste Term der Determinante ist fertig.

Natürlich verbietet niemand, die Multiplikatoren in irgendeinem Begriff (oder in allen auf einmal - warum Zeit mit Kleinigkeiten zu verschwenden?) zu tauschen, und dann werden die ersten Indizes auch eine Permutation darstellen. Aber am Ende wird sich nichts ändern: Die Gesamtzahl der Inversionen in den Indizes $ i $ und $ j $ bewahrt die Parität unter solchen Perversionen, was ganz im Einklang mit der guten alten Regel steht:

Die Neuordnung der Faktoren ändert das Produkt der Zahlen nicht.

Fügen Sie diese Regel nur nicht der Matrixmultiplikation hinzu - im Gegensatz zur Zahlenmultiplikation ist sie nicht kommutativ. Aber ich schweife ab. :)

Matrix 2x2

Tatsächlich können Sie die 1x1-Matrix betrachten - es wird eine Zelle sein, und ihre Determinante ist, wie Sie sich vorstellen können, gleich der Zahl, die in diese Zelle geschrieben wird. Nichts Interessantes.

Betrachten wir also eine 2x2-Quadratmatrix:

\ [\ links [\ begin (Matrix) ((a) _ (11)) & ((a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ Ende (Matrix) \ rechts] \]

Da die Anzahl der Zeilen darin $ n = 2 $ ist, enthält die Determinante $ n! = 2! = 1 \ cdot 2 = 2 $ Terme. Schreiben wir sie auf:

\ [\ begin (align) & ((\ left (-1 \ right)) ^ (N \ left (1; 2 \ right))) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((\ links (-1 \ rechts)) ^ (0)) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((a) _ (11)) ((a) _ (22)); \\ & ((\ links (-1 \ rechts)) ^ (N \ links (2; 1 \ rechts))) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((\ links (-1 \ rechts)) ^ (1)) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((a) _ (12)) ( (a) _ (21)). \\\ Ende (ausrichten) \]

Offensichtlich gibt es keine Inversionen in der Permutation $ \ left (1; 2 \ right) $, die aus zwei Elementen besteht, also $ N \ left (1; 2 \ right) = 0 $. Aber in der Permutation $ \ left (2; 1 \ right) $ gibt es eine Inversion (eigentlich 2< 1), поэтому $N\left(2;1 \right)=1.$

Insgesamt sieht die universelle Formel zur Berechnung der Determinante für eine 2x2-Matrix wie folgt aus:

\ [\ links | \ Anfang (Matrix) ((a) _ (11)) & ((a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ Ende ( Matrix) \ rechts | = ((a) _ (11)) ((a) _ (22)) - ((a) _ (12)) ((a) _ (21)) \]

Grafisch kann dies als Produkt der Elemente auf der Hauptdiagonalen abzüglich des Produkts der Elemente auf der Seite eins dargestellt werden:

Schauen wir uns ein paar Beispiele an:

\ [\ links | \ begin (Matrix) 5 & 6 \\ 8 & 9 \\\ Ende (Matrix) \ right |; \ quad \ left | \ begin (Matrix) 7 & 12 \\ 14 & 1 \\\ Ende (Matrix) \ right |. \]

Lösung. Alles wird in einer Zeile gezählt. Erste Matrix:

Und das zweite:

Antwort: −3; −161.

Allerdings war es zu einfach. Schauen wir uns 3x3-Matrizen an - dort ist es schon interessant.

3x3-Matrix

Betrachten Sie nun eine quadratische 3x3-Matrix:

\ [\ links [\ Anfang (Matrix) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\ ((a) _ (31)) & ((a) _ (32)) & ((a) _ (33) ) \\\ Ende (Matrix) \ rechts] \]

Wenn wir seine Determinante berechnen, erhalten wir $ 3! = 1 \ cdot 2 \ cdot 3 = 6 $-Terme - nicht zu viel für Panik, aber genug, um nach Mustern zu suchen. Schreiben wir zunächst alle Permutationen von drei Elementen auf und berechnen die Inversionen in jedem von ihnen:

\ [\ begin (align) & ((p) _ (1)) = \ left (1; 2; 3 \ right) \ Rightarrow N \ left (((p) _ (1)) \ right) = N \ links (1; 2; 3 \ rechts) = 0; \\ & ((p) _ (2)) = \ links (1; 3; 2 \ rechts) \ Pfeil rechts N \ links (((p) _ (2)) \ rechts) = N \ links (1; 3 ;2 \ rechts) = 1; \\ & ((p) _ (3)) = \ links (2; 1; 3 \ rechts) \ Pfeil rechts N \ links (((p) _ (3)) \ rechts) = N \ links (2; 1 ;3 \ rechts) = 1; \\ & ((p) _ (4)) = \ links (2; 3; 1 \ rechts) \ Pfeil rechts N \ links (((p) _ (4)) \ rechts) = N \ links (2; 3 ; 1 \ rechts) = 2; \\ & ((p) _ (5)) = \ links (3; 1; 2 \ rechts) \ Pfeil rechts N \ links (((p) _ (5)) \ rechts) = N \ links (3; 1 ;2 \ rechts) = 2; \\ & ((p) _ (6)) = \ links (3; 2; 1 \ rechts) \ Pfeil rechts N \ links (((p) _ (6)) \ rechts) = N \ links (3; 2 ; 1 \ rechts) = 3. \\\ Ende (ausrichten) \]

Wie erwartet werden sich insgesamt 6 Permutationen $ ((p) _ (1)) $, ... $ ((p) _ (6)) $ ändern), und die Anzahl der Inversionen in ihnen ändert sich von 0 zu 3.

Im Allgemeinen haben wir drei Terme mit „plus“ (wobei $ N \ left (p \ right) $ gerade ist) und drei weitere mit „minus“. Im Allgemeinen wird die Determinante nach der Formel berechnet:

\ [\ links | \ begin (Matrix) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\ ((a) _ (31)) & ((a) _ (32)) & ((a) _ (33)) \\\ Ende (Matrix) \ rechts | = \ Anfang (Matrix) ((a) _ (11)) ((a) _ (22)) ((a) _ (33)) + ((a) _ (12)) ( (a) _ (23)) ((a) _ (31)) + ((a) _ (13)) ((a) _ (21)) ((a) _ (32)) - \\ - ( (a) _ (13)) ((a) _ (22)) ((a) _ (31)) - ((a) _ (12)) ((a) _ (21)) ((a) _ (33)) - ((a) _ (11)) ((a) _ (23)) ((a) _ (32)) \\\ Ende (Matrix) \]

Setzen Sie sich einfach nicht hin und stopfen Sie jetzt wütend all diese Indizes! Anstelle von unverständlichen Zahlen ist es besser, sich die folgende Gedächtnisregel zu merken:

Dreiecksregel. Um die Determinante einer 3x3-Matrix zu finden, müssen Sie drei Produkte von Elementen auf der Hauptdiagonale und an den Scheitelpunkten gleichschenkliger Dreiecke mit einer Seite parallel zu dieser Diagonale addieren und dann dieselben drei Produkte subtrahieren, jedoch auf der Nebendiagonale. Schematisch sieht es so aus:

3x3-Matrix-Determinante: Dreiecksregel

Es sind diese Dreiecke (oder Pentagramme - was auch immer Sie bevorzugen) die sie gerne in alle möglichen Lehrbücher und Handbücher über Algebra zeichnen. Reden wir jedoch nicht über traurige Dinge. Lassen Sie uns eine solche Determinante besser berechnen - zum Aufwärmen vor echtem Zinn. :)

Aufgabe. Berechnen Sie die Determinante:

\ [\ links | \ Anfang (Matrix) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 1 \\\ Ende (Matrix) \ rechts | \]

Lösung. Wir arbeiten nach der Dreiecksregel. Zählen wir zunächst drei Terme, die aus Elementen auf der Hauptdiagonalen und parallel dazu bestehen:

\ [\ begin (ausrichten) & 1 \ cdot 5 \ cdot 1 + 2 \ cdot 6 \ cdot 7 + 3 \ cdot 4 \ cdot 8 = \\ & = 5 + 84 + 96 = 185 \\\ end (align) \]

Nun beschäftigen wir uns mit der Seitendiagonale:

\ [\ begin (ausrichten) & 3 \ cdot 5 \ cdot 7 + 2 \ cdot 4 \ cdot 1 + 1 \ cdot 6 \ cdot 8 = \\ & = 105 + 8 + 48 = 161 \\\ end (align) \]

Es bleibt nur noch die zweite von der ersten Zahl abzuziehen - und wir erhalten die Antwort:

Das ist alles!

3x3-Matrix-Determinanten sind jedoch noch nicht der Gipfel der Fähigkeiten. Das Interessanteste erwartet uns als nächstes. :)

Allgemeines Schema zur Berechnung von Determinanten

Wie wir wissen, ist die Anzahl der Terme in der Determinante mit zunehmender Dimension der Matrix $ n $ $ n! $ und wächst schnell. Trotzdem ist die Fakultät für Sie kein Mist, eine ziemlich schnell wachsende Funktion.

Schon bei 4x4-Matrizen wird es irgendwie nicht gut, die Determinanten geradeaus (d.h. durch Permutationen) abzulesen. Ich schweige im Allgemeinen über 5x5 und mehr. Daher sind einige Eigenschaften der Determinante mit dem Fall verbunden, aber es bedarf einiger theoretischer Vorbereitung, um sie zu verstehen.

Bereit? Gehen!

Was ist Matrix Minor

Gegeben sei eine beliebige Matrix $ A = \ left [m \ mal n \ right] $. Hinweis: Nicht unbedingt quadratisch. Im Gegensatz zu Determinanten sind Minderjährige solche Dinge, die nicht nur in harten quadratischen Matrizen existieren. Wählen wir mehrere (zum Beispiel $ k $) Zeilen und Spalten in dieser Matrix, mit $ 1 \ le k \ le m $ und $ 1 \ le k \ le n $. Dann:

Definition. Minor der Ordnung $ k $ ist die Determinante der quadratischen Matrix, die am Schnittpunkt der ausgewählten $ k $ Spalten und Zeilen entsteht. Wir werden diese neue Matrix auch als Minor bezeichnen.

Ein solcher Minderjähriger wird als $ ((M) _ (k)) $ bezeichnet. Natürlich kann eine Matrix eine ganze Reihe von Minderjährigen in der Größenordnung von $ k $ haben. Hier ist ein Beispiel für eine untergeordnete Ordnung 2 für die $ \ left [5 \ mal 6 \ right] $-Matrix:

Auswählen von $ k = 2 $ Spalten und Zeilen, um ein Nebenfach zu bilden

Es ist nicht erforderlich, dass die ausgewählten Zeilen und Spalten nebeneinander liegen, wie im obigen Beispiel. Die Hauptsache ist, dass die Anzahl der ausgewählten Zeilen und Spalten gleich ist (dies ist die Zahl $ k $).

Es gibt auch eine andere Definition. Vielleicht gefällt es jemand besser:

Definition. Gegeben sei eine rechteckige Matrix $ A = \ left [m \ mal n \ right] $. Wenn nach dem Löschen einer oder mehrerer Spalten und einer oder mehrerer Zeilen darin eine quadratische Matrix der Größe $ \ left [k \ mal k \ right] $ gebildet wird, dann ist ihre Determinante die kleinere $ ((M) _ (k )) $ ... Wir werden auch manchmal die Matrix selbst als Moll bezeichnen - dies wird aus dem Kontext klar.

Wie meine Katze zu sagen pflegte, ist es manchmal besser, einmal aus dem 11.

Beispiel. Gegeben eine Matrix

Wenn wir Zeile 1 und Spalte 2 wählen, erhalten wir ein Nebenfach erster Ordnung:

\ [((M) _ (1)) = \ links | 7 \ rechts | = 7 \]

Wenn wir die Zeilen 2, 3 und die Spalten 3, 4 auswählen, erhalten wir ein Moll zweiter Ordnung:

\ [((M) _ (2)) = \ links | \ Anfang (Matrix) 5 & 3 \\ 6 & 1 \\\ Ende (Matrix) \ rechts | = 5-18 = -13 \]

Und wenn Sie alle drei Zeilen sowie die Spalten 1, 2, 4 auswählen, gibt es ein Moll dritter Ordnung:

\ [((M) _ (3)) = \ links | \ begin (Matrix) 1 & 7 & 0 \\ 2 & 4 & 3 \\ 3 & 0 & 1 \\\ Ende (Matrix) \ right | \]

Für den Leser wird es nicht schwer sein, andere Minderjährige der Ordnungen 1, 2 oder 3 zu finden. Also gehen wir weiter.

Algebraische Komplemente

"Na gut, und was geben uns diese Schergen?" - Sie fragen wahrscheinlich. An sich nichts. Aber in quadratischen Matrizen hat jedes Moll einen "Begleiter" - einen zusätzlichen Moll sowie eine algebraische Ergänzung. Und zusammen ermöglichen uns diese beiden Tricks, die Qualifier wie verrückt anzuklicken.

Definition. Gegeben sei eine quadratische Matrix $ A = \ left [n \ mal n \ right] $, in der das Minor $ ((M) _ (k)) $ ausgewählt wird. Dann ist das zusätzliche Moll für das Moll $ ((M) _ (k)) $ ein Stück der ursprünglichen Matrix $ A $, das nach dem Löschen aller Zeilen und Spalten übrig bleibt, die an der Zusammensetzung des Molls beteiligt sind $ ((M) _ ( k)) $:

Zusätzlich Moll zu Moll $ ((M) _ (2)) $

Lassen Sie uns einen Punkt klarstellen: Ein zusätzliches Moll ist nicht nur ein "Stück der Matrix", sondern die Determinante dieses Stücks.

Zusätzliche Minderjährige sind mit einem Sternchen gekennzeichnet: $ M_ (k) ^ (*) $:

wobei die Operation $ A \ nabla ((M) _ (k)) $ wörtlich bedeutet "lösche von $ A $ die Zeilen und Spalten, die in $ ((M) _ (k)) $ enthalten sind". Diese Operation wird in der Mathematik nicht allgemein akzeptiert - ich habe sie nur der Schönheit der Geschichte wegen selbst erfunden. :)

Komplementäre Minderjährige werden selten allein verwendet. Sie sind Teil einer komplexeren Konstruktion - algebraischer Ergänzung.

Definition. Das Minor-Komplement $ ((M) _ (k)) $ ist das zusätzliche Minor $ M_ (k) ^ (*) $ multipliziert mit $ ((\ left (-1 \ right)) ^ (S)) $ , wobei $ S $ ist die Summe der Nummern aller Zeilen und Spalten, die im ursprünglichen Minor $ ((M) _ (k)) $ beteiligt sind.

In der Regel wird das algebraische Komplement des Molls $ ((M) _ (k)) $ mit $ ((A) _ (k)) $ bezeichnet. Deshalb:

\ [((A) _ (k)) = ((\ links (-1 \ rechts)) ^ (S)) \ cdot M_ (k) ^ (*) \]

Schwer? Auf den ersten Blick ja. Aber es ist nicht genau. Denn in Wirklichkeit ist alles einfach. Betrachten wir ein Beispiel:

Beispiel. Gegeben eine 4x4-Matrix:

Wählen wir ein Moll zweiter Ordnung

\ [((M) _ (2)) = \ links | \ begin (Matrix) 3 & 4 \\ 15 & 16 \\\ Ende (Matrix) \ right | \]

Captain Obvious deutet uns an, dass beim Verfassen dieses Molls die Zeilen 1 und 4 sowie die Spalten 3 und 4 beteiligt waren.

Es bleibt die Zahl $ S $ zu finden und das algebraische Komplement zu erhalten. Da wir die Nummern der beteiligten Zeilen (1 und 4) und Spalten (3 und 4) kennen, ist alles einfach:

\ [\ beginnen (ausrichten) & S = 1 + 4 + 3 + 4 = 12; \\ & ((A) _ (2)) = ((\ links (-1 \ rechts)) ^ (S)) \ cdot M_ (2) ^ (*) = ((\ links (-1 \ rechts) ) ^ (12)) \ cdot \ left (-4 \ right) = - 4 \ end (align) \]

Antwort: $ ((A) _ (2)) = - 4 $

Das ist alles! Tatsächlich liegt der Unterschied zwischen einem zusätzlichen Moll und einem algebraischen Komplement nur im Minus vorn und selbst dann nicht immer.

Satz von Laplace

Und so kamen wir zu dem Grund, warum all diese Minderjährigen und algebraischen Ergänzungen tatsächlich benötigt wurden.

Satz von Laplace über die Entwicklung der Determinante. Seien $ k $ Zeilen (Spalten) in einer Matrix der Größe $ \ left [n \ mal n \ right] $ ausgewählt, mit $ 1 \ le k \ le n-1 $. Dann ist die Determinante dieser Matrix gleich der Summe aller Produkte von Minoren der Ordnung $ k $, die in den ausgewählten Zeilen (Spalten) durch ihre algebraischen Komplemente enthalten sind:

\ [\ links | A \ rechts | = \ Summe (((M) _ (k)) \ cdot ((A) _ (k))) \]

Außerdem wird es genau $ C_ (n) ^ (k) $ solcher Terme geben.

Okay, okay: über $ C_ (n) ^ (k) $ - ich rede schon davon, so etwas gab es im ursprünglichen Laplace-Theorem nicht. Aber niemand hat die Kombinatorik abgesagt, und buchstäblich ein flüchtiger Blick auf den Zustand ermöglicht es Ihnen, sich selbst zu vergewissern, dass es genau so viele Begriffe geben wird. :)

Wir werden es nicht beweisen, obwohl dies keine besondere Schwierigkeit darstellt - alle Berechnungen werden auf die guten alten Permutationen und geraden / ungeraden Inversionen reduziert. Trotzdem wird der Beweis in einem separaten Absatz präsentiert, und heute haben wir eine rein praktische Lektion.

Daher gehen wir zu einem Spezialfall dieses Theorems über, wenn die Minorzellen separate Zellen der Matrix sind.

Zerlegung einer Determinante nach Zeile und Spalte

Was nun besprochen wird, ist genau das Hauptwerkzeug für die Arbeit mit Determinanten, um dessentwillen all dieses Spiel mit Permutationen, Molls und algebraischen Ergänzungen begonnen wurde.

Lesen und genießen Sie:

Korollar aus dem Satz von Laplace (Zeilen-/Spaltenentwicklung der Determinante). Es sei eine Zeile in der Matrix der Größe $ \ left [n \ mal n \ right] $ ausgewählt. Minor in dieser Zeile sind $ n $ einzelne Zellen:

\ [((M) _ (1)) = ((a) _ (ij)), \ quad j = 1, ..., n \]

Auch weitere Minderjährige sind leicht zu berechnen: Nehmen Sie einfach die Originalmatrix und löschen Sie die Zeile und Spalte mit $ ((a) _ (ij)) $. Nennen wir solche Minderjährigen $ M_ (ij) ^ (*) $.

Für das algebraische Komplement wird noch die Zahl $ S $ benötigt, aber bei einem Minor der Ordnung 1 ist dies nur die Summe der "Koordinaten" der Zelle $ ((a) _ (ij)) $:

Und dann kann die ursprüngliche Determinante gemäß dem Satz von Laplace in Form von $ ((a) _ (ij)) $ und $ M_ (ij) ^ (*) $ geschrieben werden:

\ [\ links | A \ rechts | = \ Summe \ Grenzen_ (j = 1) ^ (n) (((a) _ (ij)) \ cdot ((\ links (-1 \ rechts)) ^ (i + j)) \ cdot ((M) _ (ij))) \]

Das ist es String-Erweiterungsformel... Aber das gleiche gilt für Spalten.

Aus dieser Folgerung lassen sich mehrere Schlussfolgerungen ziehen:

1. Dieses Schema funktioniert für Zeilen und Spalten gleichermaßen gut. Tatsächlich erfolgt die Erweiterung in den meisten Fällen eher spalten- als zeilenweise.
2. Die Anzahl der Terme in der Erweiterung beträgt immer genau $ n $. Das ist deutlich weniger als $ C_ (n) ^ (k) $ und noch mehr $ n! $.
3. Statt einer Determinante $ \ left [n \ mal n \ right] $ müssen Sie mehrere Determinanten der Größe eins weniger zählen: $ \ left [\ left (n-1 \ right) \ times \ left (n-1 \ rechts) \ rechts ] $.

Letztere Tatsache ist besonders wichtig. Statt der brutalen 4x4-Determinante wird es nun zum Beispiel ausreichen, mehrere 3x3-Determinanten zu zählen - damit werden wir irgendwie fertig. :)

Aufgabe. Finden Sie die Determinante:

\ [\ links | \ Anfang (Matrix) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\ Ende (Matrix) \ rechts | \]

Lösung. Erweitern wir diese Determinante entlang der ersten Zeile:

\ [\ beginnen (ausrichten) \ links | A \ rechts | = 1 \ cdot ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | \ begin (Matrix) 5 & 6 \\ 8 & 9 \\\ end (Matrix) \ right | + & \\ 2 \ cdot ((\ left (-1 \ right)) ^ (1 + 2)) \ cdot \ links | \ begin (Matrix) 4 & 6 \\ 7 & 9 \\\ end (Matrix) \ right | + & \\ 3 \ cdot ((\ left (-1 \ right)) ^ (1 + 3)) \ cdot \ links | \ begin (Matrix) 4 & 5 \\ 7 & 8 \\\ end (Matrix) \ right | = & \\\ end (align) \]

\ [\ begin (align) & = 1 \ cdot \ left (45-48 \ right) -2 \ cdot \ left (36-42 \ right) +3 \ cdot \ left (32-35 \ right) = \\ & = 1 \ cdot \ left (-3 \ right) -2 \ cdot \ left (-6 \ right) +3 \ cdot \ left (-3 \ right) = 0. \\\ Ende (ausrichten) \]

Aufgabe. Finden Sie die Determinante:

\ [\ links | \ Anfang (Matrix) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ Ende (Matrix) \ rechts | \ ]

Lösung. Lassen Sie uns diesmal zur Abwechslung mit Spalten arbeiten. Die letzte Spalte enthält beispielsweise zwei Nullen gleichzeitig - dies reduziert natürlich die Berechnungen erheblich. Jetzt werden Sie sehen, warum.

Also erweitern wir die Determinante um die vierte Spalte:

\ [\ beginnen (ausrichten) \ links | \ Anfang (Matrix) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ Ende (Matrix) \ rechts | = 0 \ cdot ((\ left (-1 \ right)) ^ (1 + 4)) \ cdot \ left | \ begin (Matrix) 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ Ende (Matrix) \ right | + & \\ +1 \ cdot ((\ left (-1 \ rechts)) ^ (2 + 4)) \ cdot \ links | \ begin (Matrix) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ Ende (Matrix) \ right | + & \\ +1 \ cdot ((\ left (-1 \ rechts)) ^ (3 + 4)) \ cdot \ links | \ begin (Matrix) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ Ende (Matrix) \ right | + & \\ +0 \ cdot ((\ left (-1 \ rechts)) ^ (4 + 4)) \ cdot \ links | \ begin (Matrix) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\ Ende (Matrix) \ right | & \\\ Ende (ausrichten) \]

Und dann - oh, ein Wunder! - zwei Terme gehen sofort den Bach runter, da sie einen Multiplikator "0" haben. Es gibt noch zwei 3x3-Determinanten, mit denen wir leicht umgehen können:

\ [\ beginnen (ausrichten) & \ links | \ Anfang (Matrix) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ Ende (Matrix) \ rechts | = 0 + 0 + 1-1-1-0 = -1; \\ & \ links | \ Anfang (Matrix) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ Ende (Matrix) \ rechts | = 0 + 1 + 1-0-0-1 = 1. \\\ Ende (ausrichten) \]

Wir kehren zur Quelle zurück und finden die Antwort:

\ [\ links | \ begin (Matrix) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ Ende (Matrix) \ rechts | = 1 \ cdot \ left (-1 \ right) + \ left (-1 \ right) \ cdot 1 = -2 \]

Das ist also alles. Und keine 4! = 24 Begriffe mussten nicht gezählt werden. :)

Antwort: −2

Grundlegende Eigenschaften der Determinante

Im letzten Problem haben wir gesehen, wie das Vorhandensein von Nullen in den Zeilen (Spalten) einer Matrix die Entwicklung der Determinante und im Allgemeinen alle Berechnungen stark vereinfacht. Es stellt sich eine natürliche Frage: Ist es möglich, diese Nullstellen sogar in der Matrix erscheinen zu lassen, wo sie ursprünglich nicht waren?

Die Antwort ist eindeutig: kann... Und hier kommen uns die Eigenschaften der Determinante zu Hilfe:

1. Wenn Sie zwei Zeilen (Spalten) stellenweise vertauschen, ändert sich die Determinante nicht;
2. Wird eine Zeile (Spalte) mit der Zahl $ k $ multipliziert, dann wird auch die gesamte Determinante mit der Zahl $ k $ multipliziert;
3. Wenn Sie eine Zeile nehmen und sie beliebig oft von einer anderen addieren (subtrahieren), ändert sich die Determinante nicht;
4. Wenn zwei Linien der Determinante gleich sind, entweder proportional, oder eine der Linien mit Nullen gefüllt ist, dann ist die gesamte Determinante Null;
5. Alle oben genannten Eigenschaften gelten auch für Spalten.
6. Wenn eine Matrix transponiert wird, ändert sich die Determinante nicht;
7. Die Determinante des Matrixprodukts ist gleich dem Produkt der Determinanten.

Die dritte Eigenschaft ist von besonderem Wert: Wir können subtrahiere eine andere von einer Zeile (Spalte), bis Nullen an den richtigen Stellen erscheinen.

Meistens laufen die Berechnungen darauf hinaus, die gesamte Spalte überall mit Ausnahme eines Elements auf Null zu setzen und dann die Determinante entlang dieser Spalte zu erweitern, um eine Matrix von 1 kleiner zu erhalten.

Sehen wir uns an, wie das in der Praxis funktioniert:

Aufgabe. Finden Sie die Determinante:

\ [\ links | \ Anfang (Matrix) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ Ende (Matrix) \ rechts | \ ]

Lösung. Hier gibt es überhaupt keine Nullen, Sie können also auf jede Zeile oder Spalte "hämmern" - die Anzahl der Berechnungen ist ungefähr gleich. Verschwenden wir keine Zeit mit Kleinigkeiten und "null" die erste Spalte: Sie hat bereits eine Zelle mit einer, also nehmen Sie einfach die erste Zeile und subtrahieren Sie sie 4-mal von der zweiten, 3-mal von der dritten und 2-mal von der letzten.

Als Ergebnis erhalten wir eine neue Matrix, deren Determinante jedoch dieselbe ist:

\ [\ Anfang (Matrix) \ links | \ Anfang (Matrix) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ Ende (Matrix) \ rechts | \ begin (Matrix) \ Pfeil nach unten \\ -4 \\ -3 \\ -2 \\\ Ende (Matrix) = \\ = \ links | \ begin (Matrix) 1 & 2 & 3 & 4 \\ 4-4 \ cdot 1 & 1-4 \ cdot 2 & 2-4 \ cdot 3 & 3-4 \ cdot 4 \\ 3-3 \ cdot 1 & 4-3 \ cdot 2 & 1-3 \ cdot 3 & 2-3 \ cdot 4 \\ 2-2 \ cdot 1 & 3-2 \ cdot 2 & 4-2 \ cdot 3 & 1-2 \ cdot 4 \ \\ Ende (Matrix) \ rechts | = \\ = \ links | \ Anfang (Matrix) 1 & 2 & 3 & 4 \\ 0 & -7 & -10 & -13 \\ 0 & -2 & -8 & -10 \\ 0 & -1 & -2 & -7 \\ \ Ende (Matrix) \ rechts | \\\ Ende (Matrix) \]

Nun, mit Ferkels Gleichmut erweitern wir diese Determinante entlang der ersten Spalte:

\ [\ begin (Matrix) 1 \ cdot ((\ left (-1 \ right)) ^ (1 + 1)) \ cdot \ left | \ begin (Matrix) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ Ende (Matrix) \ right | +0 \ cdot ((\ links (-1 \ rechts)) ^ (2 + 1)) \ cdot \ links | ... \ rechts | + \\ +0 \ cdot ((\ links (-1 \ rechts)) ^ (3 + 1)) \ cdot \ links | ... \ rechts | +0 \ cdot ((\ left (-1 \ right)) ^ (4 + 1)) \ cdot \ left | ... \ richtig | \\\ Ende (Matrix) \]

Es ist klar, dass nur der erste Term "überleben" wird - im Rest habe ich die Determinanten nicht einmal ausgeschrieben, da sie sowieso mit Null multipliziert werden. Der Koeffizient vor der Determinante ist gleich eins, d.h. du musst es nicht aufschreiben.

Aber Sie können die "Minus" aus allen drei Zeilen der Determinante herausnehmen. Tatsächlich haben wir den Faktor (−1) dreimal herausgenommen:

\ [\ links | \ begin (Matrix) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ Ende (Matrix) \ right | = \ cdot \ left | \ Anfang (Matrix) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ Ende (Matrix) \ Rechts | \]

Wir erhalten eine kleine Determinante 3x3, die sich bereits mit der Dreiecksregel berechnen lässt. Aber wir werden versuchen, es nach der ersten Spalte zu zerlegen - zum Glück gibt es in der letzten Zeile eine:

\ [\ begin (align) & \ left (-1 \ right) \ cdot \ left | \ Anfang (Matrix) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ Ende (Matrix) \ rechts | \ Anfang (Matrix) -7 \\ -2 \\ \ Aufwärtspfeil \ \\ Ende (Matrix) = \ links (-1 \ rechts) \ cdot \ links | \ begin (Matrix) 0 & -4 & -36 \\ 0 & 4 & -4 \\ 1 & 2 & 7 \\\ Ende (Matrix) \ right | = \\ & = \ cdot \ left | \ begin (Matrix) -4 & -36 \\ 4 & -4 \\\ Ende (Matrix) \ right | = \ left (-1 \ right) \ cdot \ left | \ begin (Matrix) -4 & -36 \\ 4 & -4 \\\ Ende (Matrix) \ right | \\\ Ende (ausrichten) \]

Sie können natürlich noch etwas Spaß haben und die 2x2-Matrix in einer Reihe (Spalte) erweitern, aber wir sind ausreichend, also berechnen wir einfach die Antwort:

\ [\ links (-1 \ rechts) \ cdot \ links | \ begin (Matrix) -4 & -36 \\ 4 & -4 \\\ Ende (Matrix) \ rechts | = \ links (-1 \ rechts) \ cdot \ links (16 + 144 \ rechts) = - 160 \ ]

So werden Träume zerstört. Nur −160 in der Antwort. :)

Antwort: -160.

Ein paar Anmerkungen, bevor wir zur letzten Aufgabe kommen:

1. Die ursprüngliche Matrix war um die Seitendiagonale symmetrisch. Alle Nebenfächer in der Erweiterung sind auch um dieselbe Seitendiagonale symmetrisch.
2. Genau genommen könnten wir gar nichts erweitern, sondern die Matrix einfach auf die obere Dreiecksform bringen, wenn unter der Hauptdiagonalen feste Nullen sind. Dann ist (übrigens in exakter Übereinstimmung mit der geometrischen Interpretation) die Determinante gleich dem Produkt von $ ((a) _ (ii)) $ - Zahlen auf der Hauptdiagonalen.

Aufgabe. Finden Sie die Determinante:

\ [\ links | \ Anfang (Matrix) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ Ende (Matrix) \ rechts | \ ]

Lösung. Nun, hier bittet die erste Zeile, "nulliert" zu werden. Wir nehmen die erste Spalte und subtrahieren genau einmal von allen anderen:

\ [\ beginnen (ausrichten) & \ links | \ Anfang (Matrix) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ Ende (Matrix) \ rechts | = \\ & = \ links | \ Anfang (Matrix) 1 & 1-1 & 1-1 & 1-1 \\ 2 & 4-2 & 8-2 & 16-2 \\ 3 & 9-3 & 27-3 & 81-3 \\ 5 & ​​25-5 & 125-5 & 625-5 \\\ Ende (Matrix) \ rechts | = \ & = \ links | \ Anfang (Matrix) 1 & 0 & 0 & 0 \\ 2 & 2 & 6 & 14 \\ 3 & 6 & 24 & 78 \\ 5 & 20 & 120 & 620 \\\ Ende (Matrix) \ rechts | \\\ Ende (ausrichten) \]

Wir erweitern die erste Zeile und nehmen dann die gemeinsamen Faktoren aus den verbleibenden Zeilen heraus:

\ [\ cdot \ links | \ begin (Matrix) 2 & 6 & 14 \\ 6 & 24 & 78 \\ 20 & 120 & 620 \\\ Ende (Matrix) \ rechts | = \ cdot \ links | \ Anfang (Matrix) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ Ende (Matrix) \ Rechts | \]

Wieder beobachten wir "schöne" Zahlen, aber schon in der ersten Spalte - wir entwickeln die Determinante danach:

\ [\ begin (ausrichten) & 240 \ cdot \ left | \ begin (Matrix) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ Ende (Matrix) \ rechts | \ Anfang (Matrix) \ Pfeil nach unten \\ -1 \\ -1 \ \\ Ende (Matrix) = 240 \ cdot \ links | \ begin (Matrix) 1 & 3 & 7 \\ 0 & 1 & 6 \\ 0 & 3 & 24 \\\ Ende (Matrix) \ rechts | = \\ & = 240 \ cdot ((\ links (-1 \ rechts)) ^ (1 + 1)) \ cdot \ links | \ begin (Matrix) 1 & 6 \\ 3 & 24 \\\ Ende (Matrix) \ rechts | = \\ & = 240 \ cdot 1 \ cdot \ left (24-18 \ \\\ rechts) = 1440 \\\ end ( ausrichten) \]

Befehl. Das Problem ist gelöst worden.

Antwort: 1440

1. Allgemeine Zeichenregel. Für das Folgende ist es nützlich herauszufinden, mit welchem ​​Vorzeichen der Term in der Determinante enthalten ist, wo zwei Permutationen von Zahlen sind.

Um dies herauszufinden, sollten Sie die Faktoren in der Reihenfolge der Zeilen anordnen. Beachten Sie, dass beim Vertauschen von zwei Faktoren eine Vertauschung sowohl im ersten als auch im zweiten Index erfolgt, so dass sich die Anzahl der Inversionen im ersten Index und die Anzahl der Inversionen im zweiten Index in ungerade Zahlen ändern und sich daher ihre Summe zu ändert gerade Zahl. Daher ändert sie sich nicht bei einer Änderung der Stellen zweier Faktoren und daher bei jeder Änderung der Reihenfolge der Faktoren, da jede Änderung der Reihenfolge mehreren paarweisen Stellenwechseln entspricht. Daraus folgt, dass das Vorzeichen, mit dem der Term in die Determinante eingeht, ist. In der Tat sei die Folge der Spaltennummern, nachdem die Faktoren in die Reihenfolge der Zeilen gebracht wurden, so dass Dann

und das ist der Faktor ± 1, mit dem die für uns interessante Laufzeit in die Determinante eingeht.

2. Die Determinante der transponierten Matrix ist gleich der ursprünglichen. Mit anderen Worten, die Determinante ändert sich nicht, wenn die Matrix transponiert wird.

In der Tat ist das Nehmen der Produkte der Elemente eines aus jeder Zeile und eines aus jeder Spalte der ursprünglichen Matrix dasselbe wie in Bezug auf die transponierte Matrix. Weiterhin sind die Zeilennummern für das Original die Spaltennummern für das transponierte und die Spaltennummern für das Original sind die Zeilennummern des transponierten. Daher wird jeder Term in die Determinante der Originalmatrix aufgenommen und die Determinante mit dem gleichen Faktor transponiert

Die beiden festgelegten Eigenschaften zeigen an, dass im Qualifizierer die Zeilen und Spalten vollständig gleich sind. Daher bleiben alle weiteren für Zeilen gesetzten Eigenschaften auch für Spalten gültig.

Die nächsten beiden Eigenschaften bedeuten die Linearität der Determinante in Bezug auf die Elemente einer ihrer Linien.

3. Wenn die Elemente einer beliebigen Linie als Summe zweier Terme dargestellt werden, dann ist die Determinante gleich der Summe zweier Determinanten, in der ersten sind die Elemente der markierten Linie gleich dem ersten Addend, in der zweiten - zum zweiten.

Diese Eigenschaft wird transparenter, wenn wir von der verbalen Formulierung zur Formel übergehen:

Nachweisen.

Es ist klar, dass die erste Summe gleich ist und die zweite gleich

Die bewiesene Eigenschaft wird natürlich auf den Fall verallgemeinert, dass die Elemente einer Zeile als Summe mehrerer Terme dargestellt werden.

4. Wenn alle Elemente einer Zeile der Determinante einen gemeinsamen Faktor haben, dann kann dieser gemeinsame Faktor aus dem Vorzeichen der Determinante entnommen werden.

Wirklich,

5. Determinante mit zwei identischen Strings ist Null.

6. Wenn in der Matrix zwei Zeilen vertauscht werden, ändert ihre Determinante das Vorzeichen in das Gegenteil.

Diese beiden Eigenschaften hängen eng zusammen und spielen in der Determinantentheorie eine besonders wichtige Rolle.

Beweisen wir zuerst die 5. Eigenschaft, dann die 6.

Gegeben sei eine Determinante mit zwei identischen Geraden:

Wir teilen die Summe in zwei Teile auf, die ungeraden und geraden Permutationen entsprechen:

Denken Sie daran, dass alle ungeraden Permutationen erhalten werden, wenn die gleiche Transposition in allen geraden Permutationen durchgeführt wird.

Aber . Daher gibt es für jeden Term in der ersten Summe einen gleichen Term in der zweiten, also war dies zu beweisen.

Wenden wir uns nun dem Beweis der Eigenschaft zu und bezeichnen wir die permutierten Strings einfach mit I und II. Wir müssen Determinanten vergleichen

Betrachten Sie dazu eine Hilfsdeterminante, die a priori gleich Null ist:

Wir haben Eigenschaft 3 zweimal genutzt.

Der erste und der vierte Term sind gleich Null. Folglich ist die Summe der zweiten und dritten je nach Bedarf gleich Null.

Betrachten Sie eine andere Möglichkeit, die Eigenschaften 5 und 6 zu beweisen. Beginnen wir mit der sechsten. Lassen

Nehmen wir einen beliebigen Term aus der zweiten Determinante, geschrieben in der Reihenfolge ihrer Zeilen:

Es wird mit einem Multiplikator in die Komposition aufgenommen. Aber so geht es mit einem Multiplikator in A ein. Es ist klar, dass damit jeder Term von A mit dem entgegengesetzten Vorzeichen in A eintritt, d.h.

Um nun Eigenschaft 5 zu beweisen, betrachten wir eine Determinante mit zwei identischen Strings und kehren diese Strings um. Einerseits ändert es gleichzeitig das Vorzeichen, aber gleichzeitig ändert es sich nicht. Somit, .

Diese Argumentation ist jedoch nur anwendbar, wenn im Ring eine Division durch 2 möglich ist, also folgt aus

Auf dem Gebiet der Reste modulo 2 konnten wir eine solche Schlussfolgerung nicht ziehen. Dies ist ein kleiner Nachteil des zweiten Beweises gegenüber dem ersten.

7. Determinante mit zwei proportionalen Zeilen ist Null.

In der Tat, wenn wir gemäß Eigenschaft 4 den Proportionalitätskoeffizienten außerhalb des Vorzeichens der Determinante nehmen, dann bleibt die Determinante mit gleichen Geraden, die gleich Null ist.

8. Die Determinante ändert sich nicht, wenn zu einer ihrer Linien Zahlen hinzugefügt werden, die einer anderen Linie proportional sind.

Wirklich,

Eigenschaft 8 ist besonders wichtig, weil sie einen Schlüssel zur Berechnung von Determinanten liefert.

Schauen wir uns ein kleines Beispiel an.

Es sei erforderlich, die Determinante zu berechnen

Addiere zur zweiten Zeile den ersten multipliziert mit -1, dann den ersten multipliziert mit -1 zur dritten und dann den ersten multipliziert mit -1 zum vierten. Wir erhalten eine gleiche Determinante

Fügen Sie nun zur vierten Zeile die dritte multipliziert mit -1 und zur vierten Zeile die zweite multipliziert mit -1 hinzu.

Wir erhalten eine gleiche Determinante

Nun stellt sich heraus, dass nur einer der 24 Terme der Determinante von Null verschieden ist:. Die Permutation (1, 3, 2, 4) ist ungerade, daher ist die Determinante -16.