Vetitë përcaktuese. Ulja e rendit të përcaktorit

Disa numri llogaritet sipas një rregulli të caktuar dhe thirret përcaktues.

Nevoja për të prezantuar konceptin përcaktues - numrat duke karakterizuar katrore matrica e rendit n , lidhet ngushtë me zgjidhjen e sistemeve të ekuacioneve lineare algjebrike.

Përcaktori i një matrice A do të shënojmë: | A| ose D.

Përcaktori i matricës së rendit të parëA = (a 11) quhet element a njëmbëdhjetë . Për shembull, për A= (-4) kemi | A| = -4.

Përcaktori i një matrice të rendit të dytë thirrur numri përcaktuar nga formula

|A| = .

Për shembull, | A| = .

Me fjalë, ky rregull mund të shkruhet si më poshtë: me shenjën tuaj ju duhet të merrni produktin e elementeve të lidhur diagonale kryesore, dhe prodhimet e elementeve të lidhur me kulmet e trekëndëshave, për të cilat baza paralele me diagonalen kryesore... Me shenjën e kundërt, marrim produkte të ngjashme, vetëm në lidhje me diagonalen anësore.

Për shembull,

Përcaktimi i përcaktorit të një matrice n Ne nuk do të japim rendin e th, por vetëm do të tregojmë metodën për gjetjen e tij.

Më tej, në vend të fjalëve përcaktor i një matrice n- urdhri le të themi vetëm përcaktues n- urdhri... Le të prezantojmë koncepte të reja.

Jepet një matricë katrore n rendi i th.

Të miturM ij element a ij matricat A thirrur përcaktues (n-1) rendi i përftuar nga matrica A duke fshirë i-linja e th dhe j kolona e th.

Komplementi algjebrik А ij i elementit а ij të matricës А quhet minor i tij, marrë me shenjën (-1) i + j:

A ij = (-1) i + j M ij,

ato. një komplement algjebrik ose përkon me minorin e tij kur shuma e numrave të rreshtit dhe kolonës është numër çift, ose ndryshon prej tij në shenjë kur shuma e numrave të rreshtit dhe kolonës është një numër tek.

Për shembull, për elementët a 11 dhe a 12 matrica A = të mitur

M 11 = A 11 = ,

M 12 = ,

a A 12 = (-1) 1+2 M 12 = -8.

Teorema (mbi zgjerimin e përcaktorit) . Përcaktori i një matrice katrore është i barabartë me shumën e produkteve të elementeve të çdo rreshti (kolone) nga plotësimet e tyre algjebrike, d.m.th.

|A| = a i1 A i1 + a i2 A i2 + ... + a në A në,
për këdo i = 1, 2, …, n

|A| = a 1j A 1j + a 2j A 2j + ... + a nj A nj,

për këdo j = 1, 2, …, n

Formula e parë quhet i-rreshti i dhjetë, dhe e dyta është zgjerimi i përcaktorit në elemente j kolona e th.

Easyshtë e lehtë të kuptohet se me ndihmën e këtyre formulave ndonjë përcaktues n-rendi i mund të reduktohet në shumën e përcaktorëve, rendi i të cilave do të jetë 1 më pak, etj. derisa të arrijmë përcaktorë të rendit të tretë ose të dytë, llogaritja e të cilave nuk është më e vështirë.

Për të gjetur përcaktuesin, mund të zbatohen vetitë themelore të mëposhtme:

1. Nëse ndonjë rresht (ose kolonë) i përcaktorit përbëhet nga zero, atëherë përcaktuesi në vetvete është i barabartë me zero.

2. Kur ndërrojmë çdo dy rreshta (ose dy kolona), përcaktori shumëzohet me -1.

3. Përcaktorja me dy rreshta (ose kolona) identike ose proporcionale është e barabartë me zero.

4. Faktori i përbashkët i elementeve të çdo rreshti (ose kolone) mund të hiqet nga shenja përcaktuese.

5. Vlera e përcaktuesit nuk do të ndryshojë nëse të gjitha rreshtat dhe kolonat ndërrohen.

6. Vlera e përcaktuesit nuk do të ndryshojë nëse një rresht (kolonë) e shumëzuar me ndonjë numër i shtohet njërës prej rreshtave (ose njërës prej kolonave).

7. Shuma e produkteve të elementeve të një rreshti (ose kolone) të një matrice nga plotësimet algjebrike të elementeve të një rreshti (kolone) tjetër të kësaj matrice është e barabartë me zero.

8. Përcaktuesi i produktit të dy matricave katrore është i barabartë me produktin e përcaktuesve të tyre.

Prezantimi i nocionit të një përcaktori të një matrice na lejon të përcaktojmë një veprim më shumë me matricat - gjetjen e matricës së kundërt.

Për çdo numër jozero, ekziston një numër i kundërt i tillë që prodhimi i këtyre numrave jep një. Ekziston edhe një koncept i tillë për matricat katrore.

Matricë A-1 quhet e kundërta drejt katrore matricë A nëse shumëzojmë këtë matricë me atë të dhënë si djathtas ashtu edhe majtas jep matrica e identitetit, d.m.th.

A× A -1 = A-1 A= E.

Nga përkufizimi del se vetëm një matricë katrore ka një të anasjelltë; në këtë rast, matrica e anasjelltë do të jetë katrore e rendit të njëjtë. Megjithatë, jo çdo matricë katrore ka inversin e vet.

PLOTSIMET DHE T M MINORT ALGJERBRIK

Le të kemi një përcaktues të rendit të tretë: .

Të mitur që i përgjigjet këtij elementi një ij përcaktor i rendit të tretë, quhet përcaktor i rendit të dytë, i marrë nga e dhëna duke fshirë rreshtin dhe kolonën, në kryqëzimin e të cilave qëndron elementi i dhënë, d.m.th. i-linja e th dhe j kolona e th. Të miturit që korrespondojnë me një element të caktuar një ij do të shënojë M ij.

Për shembull, minorene M 12 që i përgjigjet elementit një 12, do të ketë një përcaktues 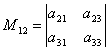, e cila fitohet duke fshirë rreshtin e parë dhe kolonën e dytë nga përcaktori i dhënë.

Kështu, formula që përcakton përcaktorin e rendit të tretë tregon se kjo përcaktor është e barabartë me shumën e prodhimeve të elementeve të rreshtit të 1-rë nga minorët përkatës; në këtë rast, minorja që i korrespondon elementit një 12, marrë me shenjën “-”, d.m.th. mund ta shkruajmë atë

Në mënyrë të ngjashme, ne mund të prezantojmë përkufizimet e të miturve për përcaktuesit e rendit të dytë dhe të rendit më të lartë.

Le të prezantojmë një koncept më shumë.

Komplement algjebrik element një ij përcaktor quhet minor i saj M ij shumëzuar me (–1) i + j.

Komplement algjebrik i një elementi një ij shënohet Një ij.

Nga përkufizimi marrim se lidhja midis plotësimit algjebrik të një elementi dhe minorit të tij shprehet me barazinë Një ij= (–1) i + j M ij.

Për shembull,

Shembull. Jepet një përcaktues. Gjej A 13, A 21, A 32.

Është e lehtë të shihet se duke përdorur plotësimet algjebrike të elementeve, formula (1) mund të shkruhet në formën:

Ngjashëm me këtë formulë, ju mund të merrni zbërthimin e përcaktorit në elementet e çdo rreshti ose kolone.

Për shembull, faktorizimi i përcaktorit nga elementët e rreshtit të 2-të mund të merret si më poshtë. Sipas vetive 2 të përcaktorit kemi:

Le të zgjerojmë përcaktuesin që rezulton me elementët e rreshtit të parë.

.

(2)

Nga këtu që nga viti përcaktorët e rendit të dytë në formulën (2) janë minoret e elementeve një 21, një 22, një 23... Kështu, d.m.th. morëm zbërthimin e përcaktorit përsa i përket elementeve të rreshtit të 2-të.

Në mënyrë të ngjashme, ju mund të merrni faktorizimin e përcaktorit për sa i përket elementeve të rreshtit të tretë. Duke përdorur vetinë 1 të përcaktorëve (rreth transpozimit), mund të tregohet se zgjerime të ngjashme janë gjithashtu të vlefshme për zgjerimin për sa i përket elementeve të kolonës.

Pra, teorema e mëposhtme është e vërtetë.

Teorema (mbi zgjerimin e një përcaktori në një rresht ose kolonë të caktuar). Përcaktori është i barabartë me shumën e produkteve të elementeve të cilitdo prej rreshtave (ose kolonave) të tij nga plotësimet e tyre algjebrike.

Të gjitha sa më sipër janë gjithashtu të vërteta për përcaktuesit e çdo niveli më të lartë.

Shembuj.

MATRICË INVERSE

Koncepti i një matrice të kundërt është prezantuar vetëm për matricat katrore.

Nëse A Pra, është një matricë katrore e kundërta për të, një matricë quhet një matricë, e shënuar A -1 dhe plotësimin e kushtit. (Ky përkufizim është paraqitur me analogji me shumëzimin e numrave)

PASURIA 1. Vlera e përcaktuesit nuk do të ndryshojë nëse të gjitha rreshtat e tij zëvendësohen me kolona, ​​dhe secila rresht zëvendësohet nga një kolonë me të njëjtin numër, domethënë

VETITË 2. Ndërrimi i dy kolonave ose i dy rreshtave të një përcaktori është i barabartë me shumëzimin e tij me -1. Për shembull,

.

VETITË 3. Nëse përcaktorja ka dy kolona identike ose dy rreshta identike, atëherë është e barabartë me zero.

VETITË 4. Shumëzimi i të gjithë elementëve të një kolone ose të një rreshti të përcaktorit me çdo numër k është i barabartë me shumëzimin e përcaktorit me këtë numër k. Për shembull,

.

VETITË 5. Nëse të gjithë elementët e një kolone ose të ndonjë rreshti janë të barabartë me zero, atëherë vetë përcaktorja është e barabartë me zero. Kjo veti është një rast i veçantë i asaj të mëparshme (për k = 0).

VETITË 6. Nëse elementet përkatëse të dy kolonave ose dy rreshtave të përcaktorit janë proporcionale, atëherë përcaktorja është e barabartë me zero.

VETITË 7. Nëse çdo element i kolonës së n-të ose rreshtit të n-të të përcaktorit është shuma e dy termave, atëherë përcaktorja mund të përfaqësohet si shuma e dy përcaktorëve, nga të cilët njëri në kolonën e n-të ose , përkatësisht, në rreshtin e n-të ka i pari nga termat e përmendur, dhe tjetri - i dyti; elementet në vendet e mbetura janë të njëjta për piketat e tre përcaktuesve. Për shembull,

VETITË 8. Nëse elementeve të ndonjë kolone (ose ndonjë rreshti) u shtojmë elementet përkatëse të një kolone tjetër (ose rreshti tjetër), të shumëzuar me ndonjë faktor të përbashkët, atëherë vlera e përcaktorit nuk do të ndryshojë. Për shembull,

.

Vetitë e mëtejshme të përcaktorëve lidhen me konceptin e një komplementi algjebrik dhe një minor. Minorja e një elementi është përcaktor që fitohet nga e dhëna duke fshirë rreshtin dhe kolonën në kryqëzimin e të cilave ndodhet ky element.

Komplementi algjebrik i çdo elementi të përcaktorit është i barabartë me minorin e këtij elementi, i marrë me shenjën e vet, nëse shuma e numrave të rreshtit dhe kolonës në kryqëzimin e së cilës ndodhet elementi është një numër çift, dhe me shenjën e kundërt nëse ky numër është tek.

Komplementin algjebrik të një elementi do ta shënojmë me një shkronjë të madhe me të njëjtin emër dhe të njëjtin numër si shkronja që përcakton vetë elementin.

PASURIA 9. Përcaktor

është e barabartë me shumën e produkteve të elementeve të çdo kolone (ose rreshti) nga plotësimet e tyre algjebrike.

Me fjalë të tjera, barazitë e mëposhtme vlejnë:

, ,

, .

6) Të miturit dhe shtesat algjebrike.

Përkufizimi. Elementi minor i përcaktorit është th porosi quhen përcaktues- rendin, i cili përftohet nga e dhëna përcaktues duke kryqëzuar rreshtin -të dhe kolonën -të në kryqëzimin e së cilës qëndron elementi.

Emërtimi:.

Përkufizimi. Komplementi algjebrik i një elementi të përcaktorit të rendit quhet minor i tij, i marrë me shenjë plus nëse është numër çift dhe me shenjë minus ndryshe.

Emërtimi:.

Teorema. (Për zgjerimin e përcaktorit.)

Përcaktori është i barabartë me shumën e produkteve të elementeve të çdo rreshti (ose çdo kolone) të përcaktorit nga plotësimet e tyre algjebrike:

7) Matrica e anasjelltë- të tilla matricë A −1 , kur shumëzohet me cilën, matrica origjinale A rezultatet ne matrica e identitetit E:

Matrica katroreështë i kthyeshëm nëse dhe vetëm nëse nuk është i gjeneruar, domethënë i tij përcaktues nuk është zero. Për matricat jo katrore dhe matricat e degjeneruara nuk ka matrica inverse. Sidoqoftë, është e mundur të përgjithësohet ky koncept dhe të prezantohet matricat pseudoinverse, e ngjashme me inversin në shumë veti.

8)Rangu i matricës- më i larti i porosive të mitur të kësaj matrice jozero

Zakonisht grada e një matricë shënohet me () ose. Të dy emërtimet na erdhën nga gjuhë të huaja, prandaj të dyja mund të përdoren.

Vetitë

Teorema (në minorën bazë): Le të jetë r = rangu A M minorja bazë e matricës A, atëherë:

rreshtat bazë dhe kolonat bazë janë linearisht të pavarura;

çdo rresht (kolonë) e matricës A është një kombinim linear i rreshtave (kolonave) bazë.

- Lëshoje ciçin deri në vdekje të sigurt!
Lëreni lirinë ta përkëdhel!
Dhe anija lundron, dhe reaktori vrumbullon ...
- Pash, a je dehur?

Mbaj mend që para klasës së 8-të nuk më pëlqente algjebra. Nuk më pëlqeu fare. Ajo më inatosi. Sepse aty nuk kuptova asgjë.

Dhe pastaj gjithçka ndryshoi, sepse kalova një pjesë:

Në matematikë në përgjithësi (dhe algjebër në veçanti), gjithçka është ndërtuar mbi një sistem kompetent dhe të qëndrueshëm të përkufizimeve. Ju i dini përkufizimet, e kuptoni thelbin e tyre - nuk do të jetë e vështirë të kuptoni pjesën tjetër.

Kështu është edhe me temën e mësimit të sotëm. Ne do të shqyrtojmë në detaje disa çështje dhe përkufizime të lidhura, falë të cilave një herë e përgjithmonë do të merreni me matricat, dhe me përcaktuesit, dhe me të gjitha vetitë e tyre.

Përcaktuesit janë një koncept qendror në algjebrën e matricës. Ashtu si formulat e shkurtuara të shumëzimit, ato do t'ju ndjekin gjatë gjithë kursit të avancuar të matematikës. Prandaj, ne lexojmë, shikojmë dhe kuptojmë plotësisht. :)

Dhe ne do të fillojmë me më intime - çfarë është një matricë? Dhe si të punoni me të saktë.

Vendosja e saktë e indekseve në matricë

Një matricë është vetëm një tabelë e mbushur me numra. Neo nuk ka asnjë lidhje me të.

Një nga karakteristikat kryesore të një matricë është dimensioni i saj, d.m.th. numri i rreshtave dhe kolonave prej të cilave përbëhet. Zakonisht thuhet se një matricë $ A $ ka madhësi $ \ majtas [m \ herë n \ djathtas] $ nëse ka $ m $ rreshta dhe $ n $ kolona. Ata e shkruajnë kështu:

Ose si kjo:

Ka emërtime të tjera - gjithçka varet nga preferencat e pedagogut / seminaristit / autorit të librit shkollor. Por në çdo rast, me të gjitha këto $ \ majtas [m \ herë n \ djathtas] $ dhe $ ((a) _ (ij)) $, ndodh i njëjti problem:

Cili indeks është përgjegjës për çfarë? Së pari është numri i rreshtit, pastaj kolona? Ose anasjelltas?

Kur lexoni leksione dhe tekste, përgjigja do të duket e qartë. Por kur keni vetëm një fletëpalosje me një problem para jush në provim, mund të dërrmoheni dhe befas të hutoheni.

Pra, le të merremi me këtë çështje një herë e përgjithmonë. Për të filluar, le të kujtojmë sistemin e zakonshëm të koordinatave nga kursi i matematikës shkollore:

Prezantimi i një sistemi koordinativ në një aeroplan

E mbani mend atë? Ka origjinën (pika $ O = \ majtas (0; 0 \ djathtas) $) akset $ x $ dhe $ y $, dhe secila pikë në aeroplan përcaktohet në mënyrë unike nga koordinatat: $ A = \ majtas (1; 2 \ djathtas) $, $ B = \ majtas (3; 1 \ djathtas) $, etj.

Tani le të marrim këtë ndërtim dhe ta vendosim pranë matricës në mënyrë që origjina të jetë në këndin e sipërm të majtë. Pse atje? Sepse kur hapim një libër, fillojmë të lexojmë pikërisht nga këndi i sipërm i majtë i faqes - është më e lehtë për t'u mbajtur mend.

Por ku duhet të drejtohen akset? Ne do t'i drejtojmë në mënyrë që e gjithë "faqja" jonë virtuale të mbulohet nga këto akse. Vërtetë, për këtë ju duhet të rrotulloni sistemin tonë të koordinatave. Mundësia e vetme e mundshme për një marrëveshje të tillë:

Tani çdo qelizë e matricës ka koordinata me vlerë të vetme $ x $ dhe $ y $. Për shembull, rekordi $ ((a) _ (24)) $ do të thotë se ne i referohemi elementit me koordinata $ x = 2 $ dhe $ y = 4 $. Dimensionet e matricës vendosen gjithashtu në mënyrë unike nga një palë numrash:

Vetëm shikoni me kujdes këtë foto. Luani me koordinatat (veçanërisht kur punoni me matrica dhe përcaktorë realë) - dhe shumë shpejt do të kuptoni se edhe në teoremat dhe përkufizimet më komplekse, ju e kuptoni në mënyrë të përsosur se çfarë është në rrezik.

Kuptohet? Epo, le të kalojmë në hapin e parë të iluminizmit - përkufizimi gjeometrik i përcaktorit. :)

Përkufizimi gjeometrik

Para së gjithash, dua të vërej se përcaktori ekziston vetëm për matricat katrore të formës $ \ majtas [n \ herë n \ djathtas] $. Një përcaktues është një numër që llogaritet sipas rregullave të caktuara dhe është një nga karakteristikat e kësaj matrice (ka karakteristika të tjera: rangu, eigenvektorët, por më shumë për këtë në mësimet e tjera).

Pra, cila është kjo karakteristikë? Çfarë do të thotë? Është e thjeshtë:

Përcaktori i një matrice katrore $ A = \ majtas [n \ herë n \ djathtas] $ është vëllimi i një paralelepipedi $ n $ -dimensionale, i cili formohet nëse i konsiderojmë rreshtat e matricës si vektorë që formojnë skajet e kësaj paralelipiped.

Për shembull, përcaktuesi i një matricë 2x2 është vetëm zona e një paralelogrami, dhe për një matricë 3x3 është tashmë vëllimi i një paralelopipedi 3 -dimensional - ai që zemëron të gjithë nxënësit e shkollave të mesme në mësimet e stereometrisë.

Në shikim të parë, ky përkufizim mund të duket plotësisht i papërshtatshëm. Por le të mos nxitojmë në përfundime - le të shohim shembuj. Në fakt, gjithçka është elementare, Watson:

Detyrë. Gjeni përcaktuesit e matricave:

\ [\ majtas | \ fillimi (matrica) 1 & 0 \\ 0 & 3 \\\ fundi (matrica) \ djathtas | \ katërkëndësh \ majtas | \ fillimi (matrica) 1 & -1 \\ 2 & 2 \\\ fundi (matrica) \ djathtas | \ katërkëndësh \ majtas | \ fillimi (matrica) 2 & 0 & 0 \\ 1 & 3 & 0 \\ 1 & 1 & 4 \\\ fundi (matrica) \ djathtas | \]

Zgjidhje. Dy kualifikueset e para janë 2x2. Pra, këto janë vetëm zonat e paralelogrameve. Le t'i vizatojmë dhe të llogarisim sipërfaqen.

Paralelogrami i parë është ndërtuar në vektorët $ ((v) _ (1)) = \ majtas (1; 0 \ djathtas) $ dhe $ ((v) _ (2)) = \ majtas (0; 3 \ djathtas) $:

Përcaktori 2x2 është zona e paralelogramit

Natyrisht, ky nuk është vetëm një paralelogram, por një drejtkëndësh. Zona e saj është

Paralelogrami i dytë është ndërtuar mbi vektorët $ ((v) _ (1)) = \ majtas (1; -1 \ djathtas) $ dhe $ ((v) _ (2)) = \ majtas (2; 2 \ djathtas ) $. Epo, çfarë? Ky është gjithashtu një drejtkëndësh:

Një tjetër përcaktues 2x2

Brinjët e këtij drejtkëndëshi (në fakt, gjatësitë e vektorëve) llogariten lehtësisht nga teorema e Pitagorës:

\ [\ fillo (rreshto) & \ majtas | ((v) _ (1)) \ djathtas | = \ sqrt (((1) ^ (2)) + ((\ \ majtas (-1 \ djathtas)) ^ (2))) = \ sqrt (2); \\ & \ majtas | ((v) _ (2)) \ djathtas | = \ sqrt (((2) ^ (2)) + ((2) ^ (2))) = \ sqrt (8) = 2 \ sqrt (2); \\ & S = \ majtas | ((v) _ (1)) \ djathtas | \ cdot \ majtas | ((v) _ (2)) \ djathtas | = \ sqrt (2) \ cdot 2 \ sqrt (2) = 4. \\\ fundi (radhis) \]

Mbetet të merremi me përcaktuesin e fundit - tashmë ekziston një matricë 3x3. Duhet të kujtojmë stereometrinë:

Përcaktori 3x3 është vëllimi i paralelopipedit

Duket thithëse e trurit, por në fakt mjafton të kujtojmë formulën për vëllimin e një paralelopipedi:

ku $ S $ është zona e bazës (në rastin tonë, kjo është zona e paralelogramit në rrafshin $ OXY $), $ h $ është lartësia e tërhequr në këtë bazë (në fakt, $ z $ -koordinata e vektorit $ ((v) _ (3)) $).

Zona e një paralelogrami (e kemi vizatuar veçmas) është gjithashtu e lehtë për t'u llogaritur:

\ [\ fillojë (radhojë) & S = 2 \ cdot 3 = 6; \\ & V = S \ cdot h = 6 \ cdot 4 = 24. \\\ fundi (radhis) \]

Kjo eshte e gjitha! Ne i shkruajmë përgjigjet.

Përgjigje: 3; 4; 24.

Një shënim i shpejtë mbi sistemin e shënimeve. Dikujt ndoshta nuk do t'i pëlqejë që unë të injoroj "shigjetat" sipër vektorëve. Me sa duket, në këtë mënyrë ju mund të ngatërroni një vektor me një pikë ose diçka tjetër.

Por le të jemi seriozë: ju dhe unë jemi tashmë djem dhe vajza të rritur, kështu që nga konteksti e kuptojmë në mënyrë të përkryer kur bëhet fjalë për një vektor dhe kur për një pikë. Shigjetat mbushin vetëm historinë, e cila tashmë është e mbushur me formula matematikore.

Dhe më tej. Në parim, asgjë nuk na pengon të marrim parasysh përcaktuesin e matricës 1x1 - një matricë e tillë është vetëm një qelizë, dhe numri i shkruar në këtë qelizë do të jetë përcaktori. Por këtu ka një shënim të rëndësishëm:

Në ndryshim nga vëllimi klasik, përcaktori do të na japë të ashtuquajturën " vëllim i orientuar", d.m.th. vëllimi, duke marrë parasysh sekuencën e shqyrtimit të vektorëve të rreshtave.

Dhe nëse doni të merrni volumin në kuptimin klasik të fjalës, duhet të merrni modulin përcaktues, por tani nuk duhet të shqetësoheni për këtë - gjithsesi, në pak sekonda do të mësojmë të numërojmë çdo përcaktor me çdo shenjë , madhësi, etj :)

Përkufizim algjebrik

Me gjithë bukurinë dhe qartësinë e qasjes gjeometrike, ajo ka një pengesë serioze: nuk na tregon asgjë se si ta llogarisim këtë shumë përcaktues.

Prandaj, tani do të analizojmë një përkufizim alternativ - algjebrik. Për ta bërë këtë, na duhet një përgatitje e shkurtër teorike, por në fund do të marrim një mjet që na lejon të numërojmë çdo gjë në matrica dhe si duam.

Vërtetë, do të ketë një problem të ri ... por së pari gjërat e para.

Permutacionet dhe përmbysjet

Le të shkruajmë numrat nga 1 në $ n $ në një rresht. Ju përfundoni me diçka të tillë:

Tani (thjesht për argëtim) ​​le të shkëmbejmë disa numra. Ju mund të ndryshoni ato ngjitur:

Ose mundeni - jo shumë fqinj:

Dhe e dini çfarë? Por asgje! Në algjebër, kjo katrahurë quhet ndërrim. Dhe ajo ka një mori pronash.

Përkufizimi. Ndërrimi i gjatësisë $ n $ është një varg $ n $ numrash të veçantë, të shkruar në çdo sekuencë. Zakonisht, konsiderohen numrat e parë $ n $ natyral (domethënë, vetëm numrat 1, 2, ..., $ n $), dhe më pas ato përzihen për të marrë zëvendësimin e dëshiruar.

Permutacionet shënohen në të njëjtën mënyrë si vektorët - vetëm një shkronjë dhe një listë vijuese e elementeve të tyre në kllapa. Për shembull: $ p = \ majtas (1; 3; 2 \ djathtas) $ ose $ p = \ majtas (2; 5; 1; 4; 3 \ djathtas) $. Shkronja mund të jetë çdo gjë, por le të jetë $ p $. :)

Më tej, për hir të thjeshtësisë, ne do të punojmë me ndërrime të gjatësisë 5 - ato janë tashmë mjaft serioze për të vëzhguar ndonjë efekt të dyshimtë, por ende jo aq të rënda për një tru të papjekur sa ndryshimet e gjatësisë 6 ose më shumë. Këtu janë shembuj të ndërrimeve të tilla:

\ [\ fillojë (rreshtoj) & ((p) _ (1)) = \ majtas (1; 2; 3; 4; 5 \ djathtas) \\ & ((p) _ (2)) = \ majtas (1 ; 3; 2; 5; 4 \ djathtas) \\ & ((p) _ (3)) = \ majtas (5; 4; 3; 2; 1 \ djathtas) \\\ fundi (radhis) \]

Natyrisht, një ndërrim i gjatësisë $ n $ mund të konsiderohet si një funksion që përcaktohet në grupin $ \ majtas \ (1; 2; ...; n \ djathtas \) $ dhe në mënyrë bijektive e harton këtë grup në vetvete. Duke iu kthyer permutacioneve të sapo shkruara të $ ((p) _ (1)) $, $ ((p) _ (2)) $ dhe $ ((p) _ (3)) $, ne mund të shkruajmë plotësisht ligjërisht:

\ [((p) _ (1)) \ majtas (1 \ djathtas) = ​​1; ((p) _ (2)) \ majtas (3 \ djathtas) = ​​2; ((p) _ (3)) \ majtas (2 \ djathtas) = ​​4; \]

Numri i permutacioneve të ndryshme të gjatësisë $ n $ është gjithmonë i kufizuar dhe i barabartë me $ n! $ - ky është një fakt lehtësisht i provueshëm nga kombinatorika. Për shembull, nëse duam të shkruajmë të gjitha permutacionet me gjatësi 5, atëherë do të jemi shumë hezitues, pasi do të ketë permutacione të tilla

Një nga karakteristikat kryesore të çdo ndryshimi është numri i përmbysjeve në të.

Përkufizimi. Inversion në ndërrim $ p = \ majtas (((a) _ (1)); ((a) _ (2)); ...; ((a) _ (n)) \ djathtas) $ - çdo çift $ \ majtas (((a) _ (i)); ((a) _ (j)) \ djathtas) $ ashtu që $ i \ lt j $, por $ ((a) _ (i)) \ gt ( ( a) _ (j)) $. E thënë thjesht, një përmbysje është kur një numër më i madh është në të majtë të një më të vogël (jo domosdoshmërisht ai ngjitur).

Ne do të shënojmë me $ N \ majtas (p \ djathtas) $ numrin e përmbysjeve në ndryshimin $ p $, por përgatituni të përmbushni emërtime të tjera në tekste të ndryshme shkollore dhe autorë të ndryshëm - këtu nuk ka standarde uniforme. Tema e përmbysjeve është shumë e gjerë dhe do t'i kushtohet një mësim i veçantë. Tani detyra jonë është thjesht të mësojmë se si t'i numërojmë ato në probleme reale.

Për shembull, le të numërojmë numrin e përmbysjeve në ndërrimin $ p = \ majtas (1; 4; 5; 3; 2 \ djathtas) $:

\ [\ majtas (4; 3 \ djathtas); \ majtas (4; 2 \ djathtas); \ majtas (5; 3 \ djathtas); \ majtas (5; 2 \ djathtas); \ majtas (3; 2 \ djathtas ). \]

Pra $ N \ majtas (p \ djathtas) = ​​5 $. Siç mund ta shihni, nuk ka asgjë të keqe me këtë. Më lejoni t'ju them menjëherë: më tej ne do të jemi të interesuar jo aq për numrin $ N \ majtas (p \ djathtas) $ sa për barazinë / çuditshmërinë e tij. Dhe këtu kalojmë pa probleme në termin kryesor të mësimit të sotëm.

Çfarë është një përcaktues

Le të jepet një matricë katrore $ A = \ majtas [n \ herë n \ djathtas] $. Pastaj:

Përkufizimi. Përcaktori i matricës $ A = \ majtas [n \ herë n \ djathtas] $ është shuma algjebrike e termave $ n!$, e përbërë si më poshtë. Çdo term është produkt i elementeve të matricës $ n $, të marra një nga secila rresht dhe çdo kolonë, shumëzuar me (−1) në fuqinë e numrit të përmbysjeve:

\ [\ majtas | A \ drejtë | = \ shuma \ kufijtë_ (n{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}

Pika themelore në zgjedhjen e faktorëve për çdo term në përcaktor është fakti se nuk ka dy faktorë në të njëjtën linjë ose në të njëjtën kolonë.

Për shkak të kësaj, ne mund të supozojmë pa humbur përgjithësinë se indekset $ i $ të faktorëve $ ((a) _ (i; j)) $ "përshkojnë" vlerat 1, ..., $ n $ , dhe indekset $ j $ janë një ndërrim i së parës:

Dhe kur ka një ndryshim $ p $, ne mund të llogarisim lehtësisht përmbysjet e $ N \ majtas (p \ djathtas) $ - dhe termi tjetër i përcaktorit është gati.

Natyrisht, askush nuk e ndalon shkëmbimin e shumëzuesve në asnjë term (ose në të gjithë menjëherë - pse të humbni kohë për gjëra të vogla?), Dhe atëherë indekset e para do të përfaqësojnë gjithashtu një ndryshim. Por në fund, asgjë nuk do të ndryshojë: numri i përgjithshëm i përmbysjeve në indekset $ i $ dhe $ j $ ruan barazinë në perversione të tilla, gjë që është mjaft në përputhje me rregullin e mirë të vjetër:

Rirregullimi i faktorëve nuk e ndryshon prodhimin e numrave.

Thjesht mos e lidhni këtë rregull me shumëzimin e matricës - ndryshe nga shumëzimi i numrave, ai nuk është komutativ. Por unë devijoj. :)

Matrica 2x2

Në fakt, mund të merrni parasysh matricën 1x1 - do të jetë një qelizë, dhe përcaktori i saj, siç mund ta merrni me mend, është i barabartë me numrin e shkruar në këtë qelizë. Asgje interesante.

Pra, le të shqyrtojmë një matricë katrore 2x2:

\ [\ majtas [\ fillojë (matrica) ((a) _ (11)) & ((a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ fundi (matrica) \ djathtas] \]

Meqenëse numri i rreshtave në të është $ n = 2 $, përcaktuesi do të përmbajë $ n! = 2! = 1 \ cdot 2 = 2 $ terma. Le t'i shkruajmë ato:

\ [\ fillojë (rreshtojë) & ((\ majtas (-1 \ djathtas)) ^ (N \ majtas (1; 2 \ djathtas))) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((\ majtas (-1 \ djathtas)) ^ (0)) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((a) _ (11)) ((a) _ (22)); \\ & ((\ majtas (-1 \ djathtas)) ^ (N \ majtas (2; 1 \ djathtas))) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((\ majtas (-1 \ djathtas)) ^ (1)) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((a) _ (12)) ( (a) _ (21)). \\\ fundi (radhis) \]

Natyrisht, nuk ka përmbysje në ndryshimin $ \ majtas (1; 2 \ djathtas) $, i cili përbëhet nga dy elementë, kështu që $ N \ majtas (1; 2 \ djathtas) = ​​0 $. Por në ndërrimin $ \ majtas (2; 1 \ djathtas) $ ka një përmbysje (në fakt, 2< 1), поэтому $N\left(2;1 \right)=1.$

Në total, formula universale për llogaritjen e përcaktorit për një matricë 2x2 duket si kjo:

\ [\ majtas | \ fillimi (matrica) ((a) _ (11)) & (a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ fundi ( matricë) \ djathtas | = ((a) _ (11)) ((a) _ (22)) - ((a) _ (12)) ((a) _ (21)) \]

Grafikisht, kjo mund të përfaqësohet si produkt i elementeve në diagonalen kryesore, pa produktin e elementeve në anën e parë:

Le të shohim disa shembuj:

\ [\ majtas | \ filloj (matricë) 5 & 6 \\ 8 & 9 \\\ fund (matricë) \ djathtas |; \ quad \ majtas | \ fillimi (matrica) 7 & 12 \\ 14 & 1 \\\ fundi (matrica) \ djathtas |. \]

Zgjidhje. Gjithçka llogaritet në një rresht. Matrica e parë:

Dhe e dyta:

Përgjigje: −3; 1161.

Megjithatë, ishte shumë e lehtë. Le të shikojmë matricat 3x3 - tashmë është interesante atje.

Matrica 3x3

Tani merrni parasysh një matricë katrore 3x3:

\ [\ majtas [\ fillojë (matrica) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\ ((a) _ (31)) & ((a) _ (32)) & (a) _ (33) ) \\\ fundi (matrica) \ djathtas] \]

Kur llogaritim përcaktuesin e tij, marrim 3 $! = 1 \ cdot 2 \ cdot 3 = 6 $ terma - jo shumë për panik, por mjaftueshëm për të filluar kërkimin për disa rregullsi. Së pari, le të shkruajmë të gjitha zëvendësimet e tre elementeve dhe të llogarisim përmbysjet në secilin prej tyre:

\ [\ filloj (rreshto) & ((p) _ (1)) = \ majtas (1; 2; 3 \ djathtas) \ Shigjeta e djathtë N \ majtas ((((p) _ (1)) \ djathtas) = ​​N \ majtas (1; 2; 3 \ djathtas) = ​​0; \\ & ((p) _ (2)) = \ majtas (1; 3; 2 \ djathtas) \ Shigjeta e djathtë N \ majtas (((p) _ (2)) \ djathtas = N \ majtas (1; 3 ; 2 \ djathtas) = ​​1; \\ & ((p) _ (3)) = \ majtas (2; 1; 3 \ djathtas) \ Shigjeta e djathtë N \ majtas (((p) _ (3)) \ djathtas = N \ majtas (2; 1 3 \ djathtas) = ​​1; \\ & ((p) _ (4)) = \ majtas (2; 3; 1 \ djathtas) \ Shigjeta djathtas N \ majtas (((p) _ (4)) \ djathtas) = ​​N \ majtas (2; 3 1 \ djathtas) = ​​2; \\ & ((p) _ (5)) = \ majtas (3; 1; 2 \ djathtas) \ Shigjeta djathtas N \ majtas (((p) _ (5)) \ djathtas) = ​​N \ majtas (3; 1 2 \ djathtas) = ​​2; \\ & ((p) _ (6)) = \ majtas (3; 2; 1 \ djathtas) \ Shigjeta djathtas N \ majtas (((p) _ (6)) \ djathtas) = ​​N \ majtas (3; 2 ; 1 \ djathtas) = ​​3. \\\ fundi (radhis) \]

Siç pritej, gjithsej 6 permutacione $ ((p) _ (1)) $, ... $ ((p) _ (6)) $ do të ndryshojnë, dhe numri i përmbysjeve në to ndryshon nga 0 në 3

Në përgjithësi, do të kemi tre terma me "plus" (ku $ N \ majtas (p \ djathtas) $ është çift) dhe tre të tjerë me "minus". Në përgjithësi, përcaktori do të llogaritet sipas formulës:

\ [\ majtas | \ filloj (matricë) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\ ((a) _ (31)) & (a) _ (32)) & ((a) _ (33)) \\\ fund (matricë) \ djathtas | = \ filloj (matricë) ((a) _ (11)) ((a) _ (22)) ((a) _ (33)) + ((a) _ (12)) ( (a) _ (23)) ((a) _ (31)) + ((a) _ (13)) ((a) _ (21)) ((a) _ (32)) - \\ - ( (a) _ (13)) ((a) _ (22)) ((a) _ (31)) - ((a) _ (12)) ((a) _ (21)) ((a) _ (33)) - ((a) _ (11)) ((a) _ (23)) ((a) _ (32)) \\\ fundi (matrica) \]

Vetëm mos u ulni dhe i grumbulloni ashpër të gjitha këto indekse tani! Në vend të numrave të pakuptueshëm, është më mirë të mbani mend rregullin e mëposhtëm mnemonik:

Rregulli i trekëndëshit. Për të gjetur përcaktuesin e një matrice 3x3, duhet të shtoni tre produkte të elementeve në diagonalen kryesore dhe në kulmet e trekëndëshave izosceles me një anë paralele me këtë diagonale, dhe më pas të zbritni të njëjtat tre produkte, por në diagonalen anësore. Skematikisht, duket kështu:

Përcaktori i matricës 3x3: Rregulla e trekëndëshit

Janë këta trekëndësha (ose pentagramë - sipas dëshirës) që u pëlqen të vizatojnë në të gjitha llojet e teksteve dhe manualeve mbi algjebër. Megjithatë, le të mos flasim për gjëra të trishtueshme. Le të llogarisim më mirë një përcaktues të tillë - për ngrohjen përpara kallajit të vërtetë. :)

Detyrë. Llogarit përcaktuesin:

\ [\ majtas | \ filloj (matricë) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 1 \\\ fund (matricë) \ djathtas | \]

Zgjidhje. Punojmë sipas rregullës së trekëndëshave. Së pari, ne numërojmë tre terma, të përbërë nga elementë në diagonalen kryesore dhe paralele me të:

\ [\ fillojë (rreshtoj) & 1 \ cdot 5 \ cdot 1 + 2 \ cdot 6 \ cdot 7 + 3 \ cdot 4 \ cdot 8 = \\ & = 5 + 84 + 96 = 185 \\\ fund (rreshtoj) \]

Tani merremi me diagonalen anësore:

\ [\ fillojë (radhis) & 3 \ cdot 5 \ cdot 7 + 2 \ cdot 4 \ cdot 1 + 1 \ cdot 6 \ cdot 8 = \\ & = 105 + 8 + 48 = 161 \\\ fund (radhis) \]

Mbetet vetëm të zbresim të dytin nga numri i parë - dhe ne do të marrim përgjigjen:

Kjo eshte e gjitha!

Sidoqoftë, përcaktuesit e matricës 3x3 nuk janë akoma kulmi i aftësive. Gjëja më interesante na pret në vazhdim. :)

Skema e përgjithshme për llogaritjen e përcaktuesve

Siç e dimë, me rritjen e dimensionit të matricës $ n $, numri i termave në përcaktues është $ n! $ Dhe rritet me shpejtësi. Në fund të fundit, faktoriali nuk është një gjë e mallkuar për ju, një funksion me rritje mjaft të shpejtë.

Tashmë për matricat 4x4, bëhet disi jo shumë e mirë leximi i përcaktuesve drejtpërsëdrejti (d.m.th. përmes permutacioneve). Rreth 5x5 dhe në përgjithësi rri i qetë. Prandaj, disa veti të përcaktuesit janë të lidhura me rastin, por një përgatitje e vogël teorike është e nevojshme për t'i kuptuar ato.

Gati? Shkoni!

Çfarë është Matrix Minor

Le të jepet një matricë arbitrare $ A = \ majtas [m \ herë n \ djathtas] $. Shënim: Jo domosdoshmërisht katror. Ndryshe nga përcaktorët, të miturit janë gjëra të tilla që ekzistojnë jo vetëm në matricat e ashpra katrore. Le të zgjedhim disa (për shembull, $ k $) rreshta dhe kolona në këtë matricë, me $ 1 \ le k \ le m $ dhe $ 1 \ le k \ le n $. Pastaj:

Përkufizimi. Minor i rendit $ k $ është përcaktuesi i matricës katrore që lind në kryqëzimin e kolonave dhe rreshtave të zgjedhur $ k $. Ne gjithashtu do ta quajmë këtë matricë të re një minore.

Një minor i tillë shënohet si $ ((M) _ (k)) $. Natyrisht, një matricë mund të ketë një grup të tërë minoresh të rendit të $ k $. Këtu është një shembull i një porosie të vogël 2 për matricën $ \ majtas [5 \ herë 6 \ djathtas] $:

Zgjedhja e $ k = 2 $ kolona dhe rreshta për të formuar një minor

Nuk është e nevojshme që rreshtat dhe kolonat e zgjedhura të jenë krah për krah, si në shembullin e mësipërm. Gjëja kryesore është se numri i rreshtave dhe kolonave të zgjedhura është i njëjtë (ky është numri $ k $).

Ekziston edhe një përkufizim tjetër. Ndoshta dikujt do t'i pëlqejë më shumë:

Përkufizimi. Le të jepet një matricë drejtkëndore $ A = \ majtas [m \ herë n \ djathtas] $. Nëse pas fshirjes së një ose disa kolonave dhe një ose disa rreshtave në të, formohet një matricë katrore me madhësi $ \ majtas [k \ herë k \ djathtas] $, atëherë përcaktori i saj është minori $ ((M) _ (k) ) $... Ne gjithashtu ndonjëherë do ta quajmë vetë matricën një minore - kjo do të jetë e qartë nga konteksti.

Siç thoshte macja ime, ndonjëherë është më mirë të zgjohesh nga kati i 11-të për të ngrënë ushqim një herë se sa të mjaullimë duke u ulur në ballkon.

Shembull. Jepet një matricë

Duke zgjedhur rreshtin 1 dhe kolonën 2, marrim një minor të rendit të parë:

\ [((M) _ (1)) = \ majtas | 7 \ djathtas | = 7 \]

Duke zgjedhur rreshtat 2, 3 dhe kolonat 3, 4, marrim një të mitur të rendit të dytë:

\ [((M) _ (2)) = \ majtas | \ fillimi (matrica) 5 & 3 \\ 6 & 1 \\\ fundi (matrica) \ djathtas | = 5-18 = -13 \]

Dhe nëse zgjidhni të tre rreshtat, si dhe kolonat 1, 2, 4, do të ketë një minoren të rendit të tretë:

\ [((M) _ (3)) = \ majtas | \ fillimi (matrica) 1 & 7 & 0 \\ 2 & 4 & 3 \\ 3 & 0 & 1 \\\ fundi (matrica) \ djathtas | \]

Nuk do të jetë e vështirë për lexuesin të gjejë të mitur të tjerë të urdhrave 1, 2 ose 3. Prandaj, le të vazhdojmë.

Komplementet algjebrike

"Epo mirë, dhe çfarë na japin këta minionë?" - ndoshta pyet. Në vetvete, asgjë. Por në matricat katrore, çdo minor ka një "shoqërues" - një minor shtesë, si dhe një plotësues algjebrik. Dhe së bashku, këto dy truke do të na lejojnë të klikojmë kualifikuesit si arra.

Përkufizimi. Le të jepet një matricë katrore $ A = \ majtas [n \ herë n \ djathtas] $, në të cilën zgjidhet minorja $ ((M) _ (k)) $. Pastaj minorja shtesë për minorin $ ((M) _ (k)) $ është një pjesë e matricës origjinale $ A $, e cila mbetet pas fshirjes së të gjitha rreshtave dhe kolonave të përfshira në kompozimin e minorit $ ((M) _ ( k)) $:

Minor shtesë në minor $ ((M) _ (2)) $

Le të sqarojmë një pikë: një minor shtesë nuk është thjesht një "pjesë e matricës", por përcaktues i kësaj pjese.

Të miturit shtesë shënohen me një yll: $ M_ (k) ^ (*) $:

ku operacioni $ A \ nabla ((M) _ (k)) $ fjalë për fjalë do të thotë "fshini nga $ A $ rreshtat dhe kolonat e përfshira në $ ((M) _ (k)) $". Ky operacion nuk pranohet përgjithësisht në matematikë - unë thjesht e shpiku atë për bukurinë e tregimit. :)

Të miturit plotësues rrallë përdoren më vete. Ato janë pjesë e një ndërtimi më kompleks, komplementit algjebrik.

Përkufizimi. Komplementi i vogël $ ((M) _ (k)) $ është minorja shtesë $ M_ (k) ^ (*) $ e shumëzuar me $ ((\ majtas (-1 \ djathtas)) ^ (S)) $ , ku $ S $ është shuma e numrave të të gjitha rreshtave dhe kolonave të përfshira në minorin origjinal $ ((M) _ (k)) $.

Si rregull, komplementi minor algjebrik $ ((M) _ (k)) $ shënohet me $ ((A) _ (k)) $. Kjo është arsyeja pse:

\ [((A) _ (k)) = ((\ majtas (-1 \ djathtas)) ^ (S)) \ cdot M_ (k) ^ (*) \]

E vështirë? Në pamje të parë, po. Por nuk është saktësisht. Sepse në realitet gjithçka është e lehtë. Le të shqyrtojmë një shembull:

Shembull. Jepet një matricë 4x4:

Le të zgjedhim një minoren të rendit të dytë

\ [((M) _ (2)) = \ majtas | \ filloj (matricë) 3 & 4 \\ 15 & 16 \\\ fund (matricë) \ djathtas | \]

Kapiteni i qartë është duke na lënë të kuptohet se rreshtat 1 dhe 4, si dhe kolonat 3 dhe 4, ishin përfshirë në përpilimin e këtij të mituri. Kryqëzojini ato - ne marrim një të mitur shtesë:

Mbetet për të gjetur numrin $ S $ dhe për të marrë komplementin algjebrik. Meqenëse i dimë numrat e rreshtave (1 dhe 4) dhe kolonave (3 dhe 4) të përfshirë, gjithçka është e thjeshtë:

\ [\ fillo (rreshto) & S = 1 + 4 + 3 + 4 = 12; \\ & ((A) _ (2)) = ((\ majtas (-1 \ djathtas)) ^ (S)) \ cdot M_ (2) ^ (*) = ((\ majtas (-1 \ djathtas) ) ^ (12)) \ cdot \ majtas (-4 \ djathtas) = ​​- 4 \ fund (rreshto) \]

Përgjigje: $ ((A) _ (2)) = - 4 $

Kjo eshte e gjitha! Në fakt, i gjithë ndryshimi midis një minoreje shtesë dhe një plotësuesi algjebrik është vetëm në minus përpara, dhe madje edhe atëherë jo gjithmonë.

Teorema e Laplasit

Dhe kështu arritëm te arsyeja pse, në fakt, nevojiteshin të gjitha këto minore dhe shtesa algjebrike.

Teorema e Laplace mbi zgjerimin e përcaktorit. Le të zgjidhen rreshtat (kolonat) $ k $ në një matricë me madhësi $ \ majtas [n \ herë n \ djathtas] $, me $ 1 \ le k \ le n-1 $. Atëherë përcaktori i kësaj matrice është i barabartë me shumën e të gjitha produkteve të të miturve të rendit $ k $ të përfshira në rreshtat (kolonat) e zgjedhura nga plotësimet e tyre algjebrike:

\ [\ majtas | A \ djathtas | = \ shuma (((M) _ (k)) \ cdot ((A) _ (k))) \]

Për më tepër, do të ketë saktësisht $ C_ (n) ^ (k) $ terma të tillë.

Mirë, në rregull: rreth $ C_ (n) ^ (k) $ - Unë tashmë po flas për të, nuk kishte asgjë të tillë në teoremën origjinale të Laplace. Por askush nuk e anuloi kombinatorikën dhe fjalë për fjalë një vështrim i përciptë i kushtit do t'ju lejojë të siguroheni vetë se do të ketë saktësisht kaq shumë terma. :)

Ne nuk do ta vërtetojmë, edhe pse kjo nuk paraqet ndonjë vështirësi të veçantë - të gjitha llogaritjet reduktohen në ndryshime të mira të vjetra dhe përmbysje çift / tek. Sidoqoftë, prova do të paraqitet në një paragraf të veçantë, dhe sot kemi një mësim thjesht praktik.

Prandaj, ne kalojmë në një rast të veçantë të kësaj teoreme, kur të miturit janë qeliza të ndara të matricës.

Zbërthimi përcaktues sipas rreshtit dhe kolonës

Ajo që do të diskutohet tani është pikërisht mjeti kryesor për të punuar me përcaktuesit, për hir të të cilit filloi e gjithë kjo lojë me ndryshime, të mitur dhe shtesa algjebrike.

Lexoni dhe shijoni:

Përfundim nga teorema e Laplasit (zgjerimi i rreshtit / kolonës së përcaktorit). Le të zgjidhet një rresht në matricën e madhësisë $ \ majtas [n \ herë n \ djathtas] $. Të miturit në këtë linjë do të jenë $ n $ qeliza individuale:

\ [((M) _ (1)) = ((a) _ (ij)), \ quad j = 1, ..., n \]

Minoret shtesë janë gjithashtu të lehta për t'u llogaritur: thjesht merrni matricën origjinale dhe fshini rreshtin dhe kolonën që përmbajnë $ ((a) _ (ij)) $. Le t'i quajmë të mitur të tillë $ M_ (ij) ^ (*) $.

Për plotësimin algjebrik, numri $ S $ është ende i nevojshëm, por në rastin e një të mituri të rendit 1, kjo është vetëm shuma e "koordinatave" të qelizës $ ((a) _ (ij)) $:

Dhe atëherë përcaktori origjinal mund të shkruhet në termat e $ ((a) _ (ij)) $ dhe $ M_ (ij) ^ (*) $ sipas teoremës së Laplace:

\ [\ majtas | A \ djathtas | = \ shuma \ limitet_ (j = 1) ^ (n) (((a) _ (ij)) \ cdot ((\ majtas (-1 \ djathtas)) ^ (i + j)) \ cdot ((M) _ (ij))) \]

Kjo është ajo që është formula e zgjerimit të vargut... Por e njëjta gjë vlen edhe për kolonat.

Nga kjo përfundim mund të nxirren disa përfundime:

1. Kjo skemë funksionon po aq mirë si për rreshtat ashtu edhe për kolonat. Në fakt, më shpesh sesa jo, zgjerimi do të jetë i mençur në kolonë sesa në atë të rreshtit.
2. Numri i termave në zgjerim është gjithmonë saktësisht $ n $. Kjo është dukshëm më pak se $ C_ (n) ^ (k) $ dhe aq më tepër $ n! $.
3. Në vend të një përcaktori $ \ majtas [n \ herë n \ djathtas] $, do t'ju duhet të numëroni disa përcaktorë të madhësisë një më pak: $ \ majtas [\ majtas (n-1 \ djathtas) \ herë \ majtas (n-1 \ djathtas) \ djathtas ] $.

Fakti i fundit është veçanërisht i rëndësishëm. Për shembull, në vend të përcaktorit brutal 4x4, tani do të jetë e mjaftueshme të numërojmë disa përcaktorë 3x3 - ne do t'i përballojmë disi. :)

Detyrë. Gjeni përcaktuesin:

\ [\ majtas | \ fillimi (matrica) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\ fundi (matrica) \ djathtas | \]

Zgjidhje. Le ta zgjerojmë këtë përcaktues përgjatë vijës së parë:

\ [\ fillojë (radhisë) \ majtas | A \ djathtas | = 1 \ cdot ((\ \ majtas (-1 \ djathtas)) ^ (1 + 1)) \ cdot \ majtas | \ fillimi (matrica) 5 & 6 \\ 8 & 9 \\\ fundi (matrica) \ djathtas | + & \\ 2 \ cdot ((\ majtas (-1 \ djathtas)) ^ (1 + 2)) \ cdot \ majtas | \ fillimi (matrica) 4 & 6 \\ 7 & 9 \\\ fundi (matrica) \ djathtas | + & \\ 3 \ cdot ((\ majtas (-1 \ djathtas)) ^ (1 + 3)) \ cdot \ majtas | \ fillimi (matrica) 4 & 5 \\ 7 & 8 \\\ fundi (matrica) \ djathtas | = & \\\ fundi (rreshtoj) \]

\ [\ fillo (rreshto) & = 1 \ cdot \ majtas (45-48 \ djathtas) -2 \ cdot \ majtas (36-42 \ djathtas) +3 \ cdot \ majtas (32-35 \ djathtas) = ​​\\ & = 1 \ cdot \ majtas (-3 \ djathtas) -2 \ cdot \ majtas (-6 \ djathtas) +3 \ cdot \ majtas (-3 \ djathtas) = ​​0. \\\ fundi (radhis) \]

Detyrë. Gjeni përcaktuesin:

\ [\ majtas | \ filloj (matricë) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ fund (matricë) \ djathtas | \ ]

Zgjidhje. Për një ndryshim, le të punojmë me kolonat këtë herë. Për shembull, kolona e fundit përmban dy zero menjëherë - padyshim, kjo do të zvogëlojë ndjeshëm llogaritjet. Tani do të shihni pse.

Pra, ne zgjerojmë përcaktorin me kolonën e katërt:

\ [\ fillojë (radhisë) \ majtas | \ filloj (matricë) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ fund (matricë) \ djathtas | = 0 \ cdot ((\ majtas (-1 \ djathtas)) ^ (1 + 4)) \ cdot \ majtas | \ fillimi (matrica) 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ fundi (matrica) \ djathtas | + & \\ +1 \ cdot ((\ majtas (-1 \ djathtas)) ^ (2 + 4)) \ cdot \ majtas | \ filloj (matricë) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ fund (matricë) \ djathtas | + & \\ +1 \ cdot ((\ \ majtas (-1 \ djathtas)) ^ (3 + 4)) \ cdot \ majtas | \ filloj (matricë) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ fund (matricë) \ djathtas | + & \\ +0 \ cdot ((\ \ majtas (-1 \ djathtas)) ^ (4 + 4)) \ cdot \ majtas | \ fillimi (matrica) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\ fundi (matrica) \ djathtas | & \\\ fundi (radhis) \]

Dhe pastaj - oh, një mrekulli! - dy terma zbresin menjëherë, pasi kanë një shumëzues "0". Ka ende dy përcaktues 3x3 me të cilët mund të trajtojmë lehtësisht:

\ [\ fillo (rreshto) & \ majtas | \ fillimi (matrica) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ fundi (matrica) \ djathtas | = 0 + 0 + 1-1-1-0 = -1; \\ & \ majtas | \ fillimi (matrica) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ fundi (matrica) \ djathtas | = 0 + 1 + 1-0-0-1 = 1. \\\ fundi (radhis) \]

Kthehemi te burimi dhe gjejmë përgjigjen:

\ [\ majtas | \ fillimi (matrica) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ fundi (matrica) \ djathtas | = 1 \ cdot \ majtas (-1 \ djathtas) + \ majtas (-1 \ djathtas) \ cdot 1 = -2 \]

Pra, kjo është e gjitha. Dhe jo 4! = 24 terma nuk duhej të numëroheshin. :)

Përgjigje: −2

Vetitë themelore të përcaktorit

Në problemin e fundit, pamë sesi prania e zerove në rreshtat (kolonat) e një matrice thjeshton shumë zgjerimin e përcaktorit dhe, në përgjithësi, të gjitha llogaritjet. Lind një pyetje e natyrshme: a është e mundur që këto zero të shfaqen edhe në matricën ku nuk ishin fillimisht?

Përgjigja është e paqartë: mund... Dhe këtu na vijnë në ndihmë vetitë e përcaktorit:

1. Nëse ndërroni dy rreshta (kolona) në vende, përcaktorja nuk do të ndryshojë;
2. Nëse një rresht (kolonë) shumëzohet me numrin $ k $, atëherë i gjithë përcaktuesi shumëzohet gjithashtu me numrin $ k $;
3. Nëse merrni një rresht dhe e shtoni (zbrisni) sa herë të doni nga një tjetër, përcaktorja nuk do të ndryshojë;
4. Nëse dy rreshta të përcaktorit janë të njëjta, ose proporcionale, ose njëra nga rreshtat është e mbushur me zero, atëherë e gjithë përcaktorja është zero;
5. Të gjitha vetitë e mësipërme janë gjithashtu të vërteta për kolonat.
6. Kur një matricë transpozohet, përcaktori nuk ndryshon;
7. Përcaktori i produktit të matricës është i barabartë me produktin e përcaktorëve.

Vetia e tretë ka një vlerë të veçantë: ne mundemi zbres një tjetër nga një rresht (kolona) derisa zerat të shfaqen në vendet e duhura.

Më shpesh, llogaritjet përfundojnë në "zeroizimin" e të gjithë kolonës kudo, përveç një elementi, dhe më pas zgjerimin e përcaktuesit përgjatë kësaj kolone, duke marrë një matricë me madhësi 1 më pak.

Le të shohim se si funksionon kjo në praktikë:

Detyrë. Gjeni përcaktuesin:

\ [\ majtas | \ fillimi (matrica) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ fundi (matrica) \\ djathtas | \ ]

Zgjidhje. Këtu nuk ka zero fare, kështu që ju mund të "goditni" në çdo rresht ose kolonë - sasia e llogaritjeve do të jetë afërsisht e njëjtë. Le të mos humbim kohë për gjëra të vogla dhe "zero" kolonën e parë: ajo tashmë ka një qelizë me një, kështu që thjesht merrni rreshtin e parë dhe zbrisni atë 4 herë nga e dyta, 3 herë nga e treta dhe 2 herë nga e fundit.

Si rezultat, do të marrim një matricë të re, por përcaktuesi i saj do të jetë i njëjtë:

\ [\ fillojë (matrica) \ majtas | \ filloj (matricë) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ fund (matricë) \ djathtas | \ fill (matricë) \ poshtë arrow \\ -4 \\ -3 \\ -2 \\\ fund (matricë) = \\ = \ majtas | \ fill (matrica) 1 & 2 & 3 & 4 \\ 4-4 \ cdot 1 & 1-4 \ cdot 2 & 2-4 \ cdot 3 & 3-4 \ cdot 4 \\ 3-3 \ cdot 1 & 4-3 \ cdot 2 & 1-3 \ cdot 3 & 2-3 \ cdot 4 \\ 2-2 \ cdot 1 & 3-2 \ cdot 2 & 4-2 \ cdot 3 & 1-2 \ cdot 4 \ \\ fundi (matrica) \ djathtas | = \\ = \ majtas | \ fillimi (matrica) 1 & 2 & 3 & 4 \\ 0 & -7 & -10 & -13 \\ 0 & -2 & -8 & -10 \\ 0 & -1 & -2 & -7 \\ \ fundi (matrica) \ djathtas | \\\ fund (matricë) \]

Tani, me ekuanitetin e Piglet, ne e zgjerojmë këtë përcaktor sipas kolonës së parë:

\ [\ filloj (matricë) 1 \ cdot ((\ \ majtas (-1 \ djathtas)) ^ (1 + 1)) \ cdot \ majtas | \ filloj (matricë) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ fund (matricë) \ djathtas | +0 \ cdot ((\ majtas (-1 \ djathtas)) ^ (2 + 1)) \ cdot \ majtas | ... \ djathtas | + \\ +0 \ cdot ((\ majtas (-1 \ djathtas)) ^ (3 + 1)) \ cdot \ majtas | ... \ djathtas | +0 \ cdot ((\ majtas (-1 \ djathtas)) ^ (4 + 1)) \ cdot \ majtas | ... \ drejtë | \\\ fundi (matricë) \]

Shtë e qartë se vetëm termi i parë do të "mbijetojë" - në pjesën tjetër as nuk i kam shkruar përcaktuesit, pasi ato gjithsesi shumëzohen me zero. Koeficienti para përcaktorit është i barabartë me një, d.m.th. nuk keni pse ta shkruani.

Por ju mund të hiqni "minuset" nga të tre rreshtat e përcaktorit. Në fakt, ne e zhvendosëm faktorin (−1) tre herë:

\ [\ majtas | \ fillimi (matrica) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ fundi (matrica) \ djathtas | = \ cdot \ majtas | \ filloj (matricë) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ fund (matricë) \ djathtas | \]

Ne morëm një përcaktues të vogël 3x3, i cili tashmë mund të llogaritet duke përdorur rregullin e trekëndëshave. Por ne do të përpiqemi ta zbërthejmë atë sipas kolonës së parë - për fat të mirë, rreshti i fundit përmban me krenari një:

\ [\ filloni (rreshtoni) & \ majtas (-1 \ djathtas) \ cdot \ majtas | \ fillimi (matrica) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ fundi (matrica) \ djathtas | \ fillimi (matrica) -7 \\ -2 \\\ lart \\ \\ fundi (matrica) = \ majtas (-1 \ djathtas) \ cdot \ majtas | \ fillimi (matrica) 0 & -4 & -36 \\ 0 & 4 & -4 \\ 1 & 2 & 7 \\\ fundi (matrica) \ djathtas | = \\ & = \ cdot \ majtas | \ fillimi (matrica) -4 & -36 \\ 4 & -4 \\\ fundi (matrica) \ djathtas | = \ majtas (-1 \ djathtas) \ cdot \ majtas | \ fillimi (matrica) -4 & -36 \\ 4 & -4 \\\ fundi (matrica) \ djathtas | \\\ fundi (radhis) \]

Sigurisht, mund të luani më shumë argëtim dhe të zgjeroni matricën 2x2 me radhë (kolona), por ne jemi adekuat, kështu që thjesht do të llogarisim përgjigjen:

\ [\ majtas (-1 \ djathtas) \ cdot \ majtas | \ fillimi (matrica) -4 & -36 \\ 4 & -4 \\\ fundi (matrica) \ djathtas | = \ majtas (-1 \ djathtas) \ cdot \ majtas (16 + 144 \ djathtas) = ​​- 160 \ ]

Kështu shkatërrohen ëndrrat. Vetëm −160 në përgjigje. :)

Përgjigje: -160.

Disa shënime përpara se të kaloni në detyrën e fundit:

1. Matrica origjinale ishte simetrike në lidhje me diagonalen anësore. Të gjitha minoret në zgjerim janë gjithashtu simetrike në lidhje me të njëjtën diagonale anësore.
2. Në mënyrë të rreptë, ne nuk mund të zgjeronim asgjë, por thjesht ta sillnim matricën në formën e sipërme trekëndore, kur ka zero të ngurta nën diagonalen kryesore. Pastaj (në përputhje të saktë me interpretimin gjeometrik, nga rruga) përcaktuesi është i barabartë me produktin e $ ((a) _ (ii)) $ - numrave në diagonalen kryesore.

Detyrë. Gjeni përcaktuesin:

\ [\ majtas | \ fillimi (matrica) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ fundi (matrica) \ djathtas | \ ]

Zgjidhje. Epo, këtu rreshti i parë kërkon të "zero". Marrim kolonën e parë dhe zbresim saktësisht një herë nga të gjitha të tjerat:

\ [\ fillo (rreshto) & \ majtas | \ filloj (matricë) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ fund (matricë) \ djathtas | = \\ & = \ majtas | \ fillojë (matrica) 1 & 1-1 & 1-1 & 1-1 \\ 2 & 4-2 & 8-2 & 16-2 \\ 3 & 9-3 & 27-3 & 81-3 \\ 5 & ​​25-5 & 125-5 & 625-5 \\\ fundi (matrica) \ djathtas | = \\ & = \ majtas | \ fillimi (matrica) 1 & 0 & 0 & 0 \\ 2 & 2 & 6 & 14 \\ 3 & 6 & 24 & 78 \\ 5 & 20 & 120 & 620 \\\ fundi (matrica) \ djathtas | \\\ fundi (radhis) \]

Zgjerohemi në rreshtin e parë, dhe më pas nxjerrim faktorët e përbashkët nga rreshtat e mbetur:

\ [\ cdot \ majtas | \ fillimi (matrica) 2 & 6 & 14 \\ 6 & 24 & 78 \\ 20 & 120 & 620 \\\ fundi (matrica) \ djathtas | = \ cdot \ majtas | \ fillimi (matrica) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ fundi (matrica) \ djathtas | \]

Përsëri vëzhgojmë numra "të bukur", por tashmë në kolonën e parë - zgjerojmë përcaktorin sipas tij:

\ [\ fillojë (radhis) & 240 \ cdot \ majtas | \ fillimi (matrica) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ fundi (matrica) \ djathtas | \ fillimi (matrica) \ poshtë \\ -1 \\ -1 \ \\ fund (matricë) = 240 \ cdot \ majtas | \ fillimi (matrica) 1 & 3 & 7 \\ 0 & 1 & 6 \\ 0 & 3 & 24 \\\ fundi (matrica) \ djathtas | = \\ & = 240 \ cdot ((\ majtas (-1 \ djathtas)) ^ (1 + 1)) \ cdot \ majtas | \ fillimi (matrica) 1 & 6 \\ 3 & 24 \\\ fundi (matrica) \ djathtas | = \\ & = 240 \ cdot 1 \ cdot \ majtas (24-18 \ djathtas) = ​​1440 \\\ fund ( rreshtoj) \]

Rendit. Problemi është zgjidhur.

Përgjigje: 1440

1. Rregulli i përgjithshëm i shenjave. Për atë që vijon, do të jetë e dobishme të zbuloni me çfarë shenje termi përfshihet në përcaktorin, ku janë dy zëvendësime numrash.

Për ta zbuluar, duhet t'i rregulloni faktorët në rendin e rreshtave. Vini re se nëse shkëmbejmë dy faktorë, atëherë ka një transpozim si në indeksin e parë ashtu edhe në indeksin e dytë, kështu që numri i inversioneve në indekset e para dhe numri i inversioneve në indekset e dyta ndryshojnë në numra tek, dhe për rrjedhojë shuma e tyre ndryshon. në një numër çift. Prandaj, nuk ndryshon me një ndryshim në vendet e dy faktorëve, dhe, rrjedhimisht, me çdo ndryshim në rendin e faktorëve, sepse çdo ndryshim në rend është ekuivalent me disa ndryshime në çift të vendeve. Nga kjo rrjedh se shenja me të cilën termi hyn në përcaktor është. Në të vërtetë, le të jetë sekuenca e numrave të kolonave pas sjelljes së faktorëve në rendin e rreshtave, në mënyrë që më pas

dhe ky është faktori ± 1, me të cilin termi me interes për ne përfshihet në përcaktor.

2. Përcaktori i matricës së transpozuar është i barabartë me atë origjinal. Me fjalë të tjera, përcaktori nuk ndryshon kur matrica transpozohet.

Në të vërtetë, marrja e produkteve të elementeve një nga çdo rresht dhe një nga çdo kolonë e matricës origjinale është njësoj si ta bësh këtë në lidhje me matricën e transpozuar. Më tej, numrat e rreshtave për origjinalin janë numrat e kolonave për atë të transpozuar, dhe numrat e kolonave për origjinalin janë numrat e rreshtave të asaj të transpozuar. Prandaj, çdo term përfshihet në përcaktorin e matricës origjinale dhe përcaktori i transpozuar me të njëjtin faktor

Dy vetitë që janë vendosur tregojnë se në kualifikues, rreshtat dhe kolonat janë plotësisht të barabarta. Prandaj, të gjitha vetitë e tjera të vendosura për rreshtat mbeten të vërteta për kolonat.

Dy vetitë e mëposhtme nënkuptojnë linearitetin e përcaktorit në lidhje me elementet e cilësdo prej rreshtave të tij.

3. Nëse elementet e ndonjë rreshti paraqiten si shumë e dy termave, atëherë përcaktorja është e barabartë me shumën e dy përcaktorëve, në të parin elementët e vijës së shënuar janë të barabartë me shtojcën e parë, në të dytën. - tek e dyta.

Kjo veti bëhet më transparente nëse kalojmë nga formulimi verbal në formulën:

Dëshmi.

Shtë e qartë se shuma e parë është e barabartë dhe e dyta është

Vetia e vërtetuar përgjithësohet natyrshëm në rastin kur elementët e një rreshti përfaqësohen si një shumë e disa termave.

4. Nëse të gjithë elementët e çdo rreshti të përcaktorit kanë një faktor të përbashkët, atëherë ky faktor i përbashkët mund të hiqet nga shenja e përcaktorit.

Vërtet,

5. Përcaktorja me dy vargje identike është zero.

6. Nëse në matricë ndërrohen dy rreshta, atëherë përcaktorja e saj do ta ndryshojë shenjën në të kundërtën.

Këto dy veti janë të lidhura ngushtë dhe luajnë një rol veçanërisht të rëndësishëm në teorinë e përcaktuesve.

Le të provojmë së pari pronën e 5-të, pastaj të 6-tën.

Le të jepet një përcaktor me dy vargje identike:

Ne e ndajmë shumën në dy pjesë që korrespondojnë me permutacionet tek dhe çift:

Kujtoni se të gjitha permutacionet tek fitohen nëse bëhet një transpozim i njëjtë në të gjitha permutacionet çift.

Por . Prandaj, për çdo term në shumën e parë, ka një term të barabartë në të dytën, kështu që kjo është ajo që kërkohej të vërtetohej.

Le t'i drejtohemi tani vërtetimit të vetive dhe le t'i shënojmë vargjet e ndërruara thjesht me I dhe II. Duhet të krahasojmë përcaktuesit

Për këtë qëllim, merrni parasysh një përcaktues ndihmës, i cili është apriori i barabartë me zero:

Pronën e kemi shfrytëzuar 3 dy herë.

Termat e parë dhe të katërt janë të barabartë me zero. Rrjedhimisht, shuma e dytë dhe e tretë është e barabartë me zero, siç kërkohet.

Konsideroni një mënyrë tjetër për të vërtetuar vetitë 5 dhe 6. Le të fillojmë me të gjashtën. Le te jete

Merrni çdo term nga përcaktori i dytë, i shkruar sipas renditjes së rreshtave të tij:

Përfshihet me një shumëzues. Por, pra hyn në A me një shumëzues. Është e qartë se kështu që çdo term nga A hyn në A me shenjën e kundërt, d.m.th.

Tani, për të vërtetuar vetinë 5, merrni parasysh një përcaktor me dy vargje identike dhe ktheni këto vargje. Nga njëra anë, do të ndryshojë shenjën në të njëjtën kohë, por në të njëjtën kohë nuk do të ndryshojë. Prandaj, .

Megjithatë, ky arsyetim është i zbatueshëm vetëm nëse ndarja me 2 është e mundur në unazë, kështu që rrjedh nga

Në fushën e mbetjeve modulo 2, ne nuk mund të nxjerrim një përfundim të tillë. Kjo është një e metë e lehtë në provën e dytë në krahasim me të parën.

7. Përcaktorja me dy rreshta proporcionale është zero.

Në të vërtetë, nëse, sipas vetive 4, marrim koeficientin e proporcionalitetit përtej shenjës së përcaktorit, atëherë mbetet përcaktorja me drejtëza të barabarta, e cila është e barabartë me zero.

8. Përcaktorja nuk ndryshon nëse në ndonjë nga rreshtat e saj shtoni numra proporcionalë me një rresht tjetër.

Vërtet,

Vetia 8 është veçanërisht e rëndësishme sepse siguron një çelës për llogaritjen e përcaktuesve.

Le të shohim një shembull të vogël.

Le të kërkohet llogaritja e përcaktorit

Shtoni në rreshtin e dytë të parën shumëzuar me -1, pastaj shtoni të parën shumëzuar me -1 në të tretën dhe pastaj shtoni të parën shumëzuar me -1 në të katërtin. Ne marrim një përcaktues të barabartë

Tani shtoni në rreshtin e katërt të tretën shumëzuar me -1, dhe në rreshtin e katërt të dytën shumëzuar me -1.

Marrim një përcaktor të barabartë

Tani rezulton se vetëm një nga 24 termat e përcaktorit është jozero:. Permutacioni (1, 3, 2, 4) është tek, prandaj përcaktorja është -16.