Një funksion linear i një ndryshoreje komplekse z është një funksion i formës ku a dhe 6 janë dhënë numra kompleks, dhe një F 0. Një funksion linear përcaktohet për të gjitha vlerat e ndryshores së pavarur z, është me një vlerë dhe , meqenëse funksioni i anasjelltë është gjithashtu me një vlerë, ai është njëvalent në të gjithë rrafshin z. Një funksion linear është analitik në të gjithë rrafshin kompleks dhe rrjedhimisht derivati ​​i tij është konform me hartëzimin e kryer prej tij në të gjithë rrafshin. Një funksion linear-fraksional është një funksion i numrave kompleksë të dhënë nga forma, dhe një funksion linear-fraksional është përcaktuar për të gjitha vlerat e ndryshores së pavarur zy, përveç z = -|, është me një vlerë dhe, meqenëse anasjelltas Funksioni Funksionet elementare të një ndryshoreje komplekse Funksionet thyesore-racionale Funksioni i fuqisë Funksioni eksponencial Funksioni logaritmik Funksionet trigonometrike dhe hiperbolike janë me një vlerë, njëvalente në të gjithë rrafshin kompleks, duke përjashtuar pikën z = - Në këtë rajon, funksioni (3) është analitike dhe derivati ​​i saj, pra, hartëzimi i kryer prej tij është konform. Le ta zgjerojmë funksionin (3) në pikën z = - \, duke vendosur t) = oo, dhe ta vendosim pikën në pafundësi w = oo në korrespondencë me pikën z(oo) = Atëherë funksioni linear-fraksional do të jetë njëvalent në planin kompleks të zgjeruar z. Shembulli 1. Konsideroni një funksion linear- thyesor Nga barazia rezulton se modulët e numrave kompleks r dhe u janë të lidhur me relacionin dhe vetë këta numra janë të vendosur në rrezet që dalin nga pika O dhe janë simetrik në lidhje me boshtin real. Në veçanti, pikat e rrethit njësi |z| = 1 shkojnë në pikat e rrethit njësi N = 1. Në këtë rast, numri i konjuguar i caktohet numrit kompleks (Fig. 11). Vini re gjithashtu se funksioni r0 = -g paraqet pikën në pafundësi r - oo në zero r0 - 0. 2.2. Funksioni i fuqisë Një funksion fuqie ku n është një numër natyror, është analitik në të gjithë rrafshin kompleks; derivati ​​i tij = nzn~] për η > 1 është jo zero në të gjitha pikat përveç z = 0. Duke shkruar w dhe z në formulën (4) në formë eksponenciale, marrim se nga formula (5) mund të shihet se kompleksi numrat Z\ dhe z2 të tillë që ku k është një numër i plotë shkojnë në një pikë w. Prandaj, për n > 1 hartëzimi (4) nuk është njëvalent në planin z. Shembulli më i thjeshtë i një domeni në të cilin pasqyrimi ri = zn është njëvalent është sektori ku a është çdo numër real. Në rajonin (7), hartëzimi (4) është konform. - është me shumë vlera, sepse për çdo numër kompleks z \u003d r1v Ф 0, mund të specifikoni n numra kompleks të ndryshëm, të tillë që shkalla e n-të e tyre të jetë e barabartë me z: Vini re se polinomi i shkallës n i një ndryshoreje komplekse z është një funksion ku jepen numra kompleks, dhe ao Ф 0. Një polinom i çdo shkalle është një funksion analitik në të gjithë planin kompleks. 2.3. Funksioni thyesor-racional Një funksion thyesor-racional është një funksion i formës ku) janë polinome të një ndryshoreje komplekse z. Një funksion racional thyesor është analitik në të gjithë rrafshin, me përjashtim të atyre pikave ku emëruesi Q(z) zhduket. Shembulli 3. Funksioni Zhukovsky është analitik në të gjithë rrafshin z, duke përjashtuar pikën z = 0. Le të zbulojmë kushtet në rajonin e rrafshit kompleks në të cilin funksioni Zhukovsky i konsideruar në këtë rajon do të jetë njëvalent. M Le të barten pikat Z) dhe zj nga funksioni (8) në një pikë. Pastaj, për , marrim se Prandaj, për njëvalencën e funksionit Zhukovsky, është e nevojshme dhe e mjaftueshme që kushti të plotësohet.Një shembull i një domeni që plotëson kushtin e njëvlershmërisë (9) është pjesa e jashtme e rrethit |z| > 1. Meqenëse derivati ​​i funksionit Zhukovsky Funksionet elementare të një ndryshoreje komplekse Funksionet thyesore-racionale Funksioni i fuqisë Funksioni eksponencial Funksioni logaritmik Funksionet trigonometrike dhe hiperbolike janë jo zero kudo, përveç pikave, atëherë hartëzimi i zonës që kryhet nga ky funksion do të jetë konformale (Fig. 13). Vini re se brendësia e njësisë diskut |I është gjithashtu domeni i njëvalencës së funksionit Zhukovsky. Oriz. 13 2.4. Funksioni eksponencial Ne përcaktojmë funksionin eksponencial ez për çdo numër kompleks z = x + y si më poshtë: Për x = 0 marrim formulën e Euler-it: Le të përshkruajmë vetitë kryesore të funksionit eksponencial: 1. Për z real, ky përkufizim përkon me atë të zakonshmen. Kjo mund të verifikohet drejtpërdrejt duke vendosur y = 0 në formulën (10) 2. Funksioni ez është analitik në të gjithë rrafshin kompleks dhe për të ruhet formula e zakonshme e diferencimit 3. Teorema e mbledhjes ruhet për funksionin ez . Le të 4. Funksioni ez është periodik me periudhën kryesore imagjinare 2xi. Në të vërtetë, për çdo numër të plotë k Nga ana tjetër, nëse atëherë nga përkufizimi (10) rrjedh se nga rrjedh se, ose ku n është një numër i plotë. Shiriti nuk përmban një çift të vetëm pikash të lidhura me relacionin (12), kështu që nga studimi rezulton se pasqyrimi w = e" është njëvalent në shirit (Fig. 14). Meqenëse është derivat, ky pasqyrim është Vërejtje niv Funksioni rg është njëvalent në çdo shirit 2.5 Funksioni logaritmik Nga ekuacioni ku është dhënë, e panjohura, marrim Pra, funksioni i kundërt i funksionit përcaktohet për çdo dhe përfaqësohet me formulën ku Ky shumë- Funksioni me vlerë quhet logaritmik dhe shënohet si më poshtë shënojmë me Pastaj formula 2 fitohet për Ln z. 6. Funksionet trigonometrike dhe hiperbolike Nga formula e Euler-it (11) për y real ne marrim nga. Ne përcaktojmë funksionet trigonometrike sin z dhe cos z për çdo numër kompleks z duke përdorur formulat e mëposhtme: Sinusi dhe kosinusi i një argumenti kompleks kanë veti interesante. . Le të rendisim ato kryesore. Funksionet sinz dhe cos z: 1) për z real -x përkojnë me sinuset dhe kosinuset e zakonshme; 2) janë analitike në të gjithë planin kompleks; 3) respektoni formulat e zakonshme të diferencimit: 4) janë periodike me një periudhë 2n; 5) sin z - funksion tek, a cos z - çift; 6) janë ruajtur marrëdhëniet e zakonshme trigonometrike. Të gjitha vetitë e listuara merren lehtësisht nga formula (15). Funksionet tgz dhe ctgz në fushën komplekse përcaktohen me formula, dhe funksionet hiperbolike përcaktohen me formulat "Funksionet hiperbolike janë të lidhura ngushtë me funksionet trigonometrike. Kjo marrëdhënie shprehet me barazitë e mëposhtme: Sinusi dhe kosinusi i një argumenti kompleks kanë një veti tjetër e rëndësishme: në planin kompleks Shembulli 4. Është e lehtë të kontrollohet se -4 ,

Funksionet e një ndryshoreje komplekse.
Diferencimi i funksioneve të një ndryshoreje komplekse.

Ky artikull hap një seri mësimesh në të cilat do të shqyrtoj problemet tipike që lidhen me teorinë e funksioneve të një ndryshoreje komplekse. Për të zotëruar me sukses shembujt, duhet të keni njohuri bazë për numrat kompleks. Për të konsoliduar dhe përsëritur materialin, mjafton të vizitoni faqen. Ju gjithashtu do të keni nevojë për aftësi për të gjetur derivatet e pjesshme të rendit të dytë. Ja ku janë, këto derivate të pjesshme ... edhe tani u habita pak sa shpesh ndodhin ...

Tema që po fillojmë të analizojmë nuk është veçanërisht e vështirë, dhe në funksionet e një ndryshoreje komplekse, në parim, gjithçka është e qartë dhe e arritshme. Gjëja kryesore është t'i përmbahemi rregullit bazë, i cili rrjedh nga unë në mënyrë empirike. Lexo!

Koncepti i një funksioni të një ndryshoreje komplekse

Së pari, le të rifreskojmë njohuritë tona rreth funksionit shkollor të një ndryshoreje:

Funksioni i një ndryshorejeështë një rregull sipas të cilit çdo vlerë e ndryshores së pavarur (nga fusha e përkufizimit) i përgjigjet një dhe vetëm një vlere të funksionit. Natyrisht, "x" dhe "y" janë numra realë.

Në rastin kompleks, varësia funksionale jepet në mënyrë të ngjashme:

Funksioni me një vlerë të një ndryshoreje komplekseështë rregulli që të gjithë gjithëpërfshirëse vlera e ndryshores së pavarur (nga domeni) i përgjigjet një dhe të vetme gjithëpërfshirëse vlera e funksionit. Në teori, konsiderohen gjithashtu funksione me shumë vlera dhe disa lloje të tjera, por për thjeshtësi, unë do të përqendrohem në një përkufizim.

Cili është funksioni i një ndryshoreje komplekse?

Dallimi kryesor është se numrat janë kompleks. Nuk po ironizoj. Nga pyetje të tilla ata shpesh bien në hutim, në fund të artikullit do të tregoj një histori të lezetshme. Në mësim Numrat kompleksë për dummies kemi konsideruar një numër kompleks në formën . Që tani shkronja "Z" është bërë e ndryshueshme, atëherë do ta shënojmë si më poshtë: , ndërsa "x" dhe "y" mund të marrin të ndryshme e vlefshme vlerat. Përafërsisht, funksioni i një ndryshoreje komplekse varet nga variablat dhe , të cilat marrin vlera "të zakonshme". Pika e mëposhtme rrjedh logjikisht nga ky fakt:

Funksioni i një ndryshoreje komplekse mund të shkruhet si:
, ku dhe janë dy funksione të dy e vlefshme variablave.

Funksioni thirret pjesë reale funksione .
Funksioni thirret pjesë imagjinare funksione .

Domethënë, funksioni i një ndryshoreje komplekse varet nga dy funksione reale dhe . Për të sqaruar më në fund gjithçka, le të shohim shembuj praktikë:

Shembulli 1

Zgjidhja: Ndryshorja e pavarur "z", siç e mbani mend, shkruhet si, pra:

(1) Zëvendësuar në funksionin origjinal.

(2) Për termin e parë, u përdor formula e shumëzimit të reduktuar. Në mandat u hapën kllapat.

(3) Me kujdes katror, ​​duke mos harruar këtë

(4) Rirregullimi i termave: së pari rishkruaj termat , në të cilën nuk ka një njësi imagjinare(grupi i parë), pastaj termat, ku ka (grupi i dytë). Duhet të theksohet se nuk është e nevojshme të përzihen termat dhe ky hap mund të anashkalohet (në fakt, duke e kryer atë me gojë).

(5) Grupi i dytë nxirret nga kllapa.

Si rezultat, funksioni ynë doli të përfaqësohej në formë

Përgjigje:
është pjesa reale e funksionit.
është pjesa imagjinare e funksionit .

Cilat janë këto funksione? Funksionet më të zakonshme të dy variablave, nga të cilat mund të gjenden kaq të njohura derivatet e pjesshme. Pa mëshirë - do të gjejmë. Por pak më vonë.

Shkurtimisht, algoritmi i problemit të zgjidhur mund të shkruhet si më poshtë: ne zëvendësojmë në funksionin origjinal, kryejmë thjeshtime dhe ndajmë të gjithë termat në dy grupe - pa një njësi imagjinare (pjesa reale) dhe me një njësi imagjinare (pjesa imagjinare).

Shembulli 2

Gjeni pjesën reale dhe imagjinare të një funksioni

Ky është një shembull bëjeni vetë. Përpara se të hidheni në betejë në aeroplanin kompleks me damë të zhveshur, më lejoni t'ju jap këshillat më të rëndësishme për këtë temë:

BEJ KUJDES! Duhet të jeni të kujdesshëm, natyrisht, kudo, por në numra komplekse duhet të jeni më të kujdesshëm se kurrë! Mos harroni se, zgjeroni me kujdes kllapat, mos humbisni asgjë. Sipas vëzhgimeve të mia, gabimi më i zakonshëm është humbja e shenjës. Mos u ngut!

Zgjidhje e plotë dhe përgjigje në fund të mësimit.

Tani kubike. Duke përdorur formulën e shkurtuar të shumëzimit, ne nxjerrim:
.

Formulat janë shumë të përshtatshme për t'u përdorur në praktikë, pasi ato shpejtojnë shumë procesin e zgjidhjes.

Diferencimi i funksioneve të një ndryshoreje komplekse.

Kam dy lajme: të mira dhe të këqija. Do të filloj me një të mirë. Për një funksion të një ndryshoreje komplekse vlejnë rregullat e diferencimit dhe tabela e derivateve të funksioneve elementare. Kështu, derivati ​​merret në të njëjtën mënyrë si në rastin e një funksioni të një ndryshoreje reale.

Lajmi i keq është se për shumë funksione të një ndryshoreje komplekse, nuk ka fare derivat dhe ju duhet të kuptoni është i diferencueshëm një funksion apo një tjetër. Dhe "të kuptoni" se si ndihet zemra juaj shoqërohet me telashe shtesë.

Konsideroni një funksion të një ndryshoreje komplekse. Që ky funksion të jetë i diferencueshëm, është e nevojshme dhe e mjaftueshme që:

1) Që të ketë derivate të pjesshëm të rendit të parë. Harrojini këto shënime menjëherë, pasi në teorinë e funksionit të një ndryshoreje komplekse, tradicionalisht përdoret një version tjetër i shënimit: .

2) Për të kryer të ashtuquajturat Kushtet e Cauchy-Riemann:

Vetëm në këtë rast derivati ​​do të ekzistojë!

Shembulli 3

Zgjidhje zbërthehet në tre faza të njëpasnjëshme:

1) Gjeni pjesët reale dhe imagjinare të funksionit. Kjo detyrë u analizua në shembujt e mëparshëm, kështu që unë do ta shkruaj pa koment:

Që atëherë:

Në këtë mënyrë:

është pjesa imagjinare e funksionit .

Do të ndalem në një pikë tjetër teknike: në çfarë rendi shkruani termat në pjesë reale dhe imagjinare? Po, në thelb nuk ka rëndësi. Për shembull, pjesa reale mund të shkruhet kështu: , dhe imagjinare - si kjo: .

2) Le të kontrollojmë përmbushjen e kushteve Cauchy-Riemann. Janë dy prej tyre.

Le të fillojmë duke kontrolluar gjendjen. Ne gjejme derivatet e pjesshme:

Kështu, kushti plotësohet.

Pa dyshim, lajmi i mirë është se derivatet e pjesshme janë pothuajse gjithmonë shumë të thjeshta.

Ne kontrollojmë përmbushjen e kushtit të dytë:

Doli e njëjta gjë, por me shenja të kundërta, pra plotësohet edhe kushti.

Kushtet Cauchy-Riemann plotësohen, prandaj funksioni është i diferencueshëm.

3) Gjeni derivatin e funksionit. Derivati ​​është gjithashtu shumë i thjeshtë dhe gjendet sipas rregullave të zakonshme:

Njësia imagjinare në diferencim konsiderohet konstante.

Përgjigje: - pjesa reale është pjesa imagjinare.
Kushtet Cauchy-Riemann janë plotësuar,.

Ka dy mënyra të tjera për të gjetur derivatin, ato natyrisht përdoren më rrallë, por informacioni do të jetë i dobishëm për të kuptuar mësimin e dytë - Si të gjeni funksionin e një ndryshoreje komplekse?

Derivati ​​mund të gjendet duke përdorur formulën:

Në këtë rast:

Në këtë mënyrë

Është e nevojshme të zgjidhet problemi i kundërt - në shprehjen që rezulton, ju duhet të izoloni . Për ta bërë këtë, është e nevojshme në terma dhe të nxirren nga kllapat:

Veprimi i kundërt, siç kanë vënë re shumë, është disi më i vështirë për t'u kryer, për verifikim është gjithmonë më mirë të merret shprehja dhe në draft ose të hapni verbalisht kllapat prapa, duke u siguruar që do të dalë saktësisht

Formula e pasqyrës për gjetjen e derivatit:

Në këtë rast: , Kjo është arsyeja pse:

Shembulli 4

Përcaktoni pjesët reale dhe imagjinare të një funksioni . Kontrolloni përmbushjen e kushteve të Cauchy-Riemann. Nëse plotësohen kushtet Cauchy-Riemann, gjeni derivatin e funksionit.

Një zgjidhje e shkurtër dhe një mostër e përafërt e përfundimit në fund të mësimit.

A përmbushen gjithmonë kushtet Cauchy-Riemann? Teorikisht, ato më shpesh nuk përmbushen se sa janë. Por në shembuj praktikë, nuk mbaj mend një rast që ato të mos ishin ekzekutuar =) Kështu, nëse derivatet tuaja të pjesshme "nuk u konvergjuan", atëherë me një probabilitet shumë të lartë mund të themi se keni bërë një gabim diku.

Le të komplikojmë funksionet tona:

Shembulli 5

Përcaktoni pjesët reale dhe imagjinare të një funksioni . Kontrolloni përmbushjen e kushteve të Cauchy-Riemann. Llogaritni

Zgjidhja: Algoritmi i zgjidhjes ruhet plotësisht, por në fund shtohet një modë e re: gjetja e derivatit në një pikë. Për kubin, formula e kërkuar tashmë është nxjerrë:

Le të përcaktojmë pjesët reale dhe imagjinare të këtij funksioni:

Vëmendje dhe sërish vëmendje!

Që atëherë:


Në këtë mënyrë:
është pjesa reale e funksionit;
është pjesa imagjinare e funksionit .

Kontrollimi i kushtit të dytë:

Doli e njëjta gjë, por me shenja të kundërta, pra plotësohet edhe kushti.

Kushtet Cauchy-Riemann plotësohen, prandaj funksioni është i diferencueshëm:

Llogaritni vlerën e derivatit në pikën e kërkuar:

Përgjigje:, , kushtet Cauchy-Riemann janë të kënaqur,

Funksionet me kube janë të zakonshme, kështu që një shembull për t'u konsoliduar:

Shembulli 6

Përcaktoni pjesët reale dhe imagjinare të një funksioni . Kontrolloni përmbushjen e kushteve të Cauchy-Riemann. Llogarit .

Vendimi dhe përfundimi i mostrës në fund të mësimit.

Në teorinë e analizës komplekse përcaktohen edhe funksionet e tjera të argumentit kompleks: eksponencial, sinus, kosinus etj. Këto funksione kanë veti të pazakonta dhe madje të çuditshme - dhe është vërtet interesante! Unë me të vërtetë dua t'ju them, por këtu, ashtu ndodhi, jo një libër referimi ose një tekst shkollor, por një zgjidhje, kështu që do të shqyrtoj të njëjtën detyrë me disa funksione të përbashkëta.

Së pari në lidhje me të ashtuquajturat Formulat e Euler-it:

Për këdo e vlefshme numrat, formulat e mëposhtme janë të vlefshme:

Ju gjithashtu mund ta kopjoni atë në fletoren tuaj si referencë.

Në mënyrë të rreptë, ekziston vetëm një formulë, por zakonisht, për lehtësi, ata gjithashtu shkruajnë një rast të veçantë me një minus në tregues. Parametri nuk duhet të jetë një shkronjë e vetme, ai mund të jetë një shprehje komplekse, një funksion, është e rëndësishme vetëm që ato të marrin vetëm e vlefshme vlerat. Në fakt, ne do ta shohim atë tani:

Shembulli 7

Gjeni derivatin.

Zgjidhja: Linja e përgjithshme e partisë mbetet e palëkundur - është e nevojshme të veçohen pjesët reale dhe imagjinare të funksionit. Unë do të jap një zgjidhje të detajuar dhe do të komentoj për secilin hap më poshtë:

Që atëherë:

(1) Zëvendësim për "z".

(2) Pas zëvendësimit, është e nevojshme të ndahen pjesët reale dhe imagjinare i pari në eksponent ekspozuesit. Për ta bërë këtë, hapni kllapat.

(3) Ne grupojmë pjesën imagjinare të treguesit, duke e vendosur njësinë imagjinare jashtë kllapave.

(4) Përdorni veprimin e shkollës me fuqi.

(5) Për shumëzuesin, ne përdorim formulën e Euler-it, ndërsa .

(6) Ne hapim kllapat, si rezultat:

është pjesa reale e funksionit;
është pjesa imagjinare e funksionit .

Veprimet e mëtejshme janë standarde, le të kontrollojmë përmbushjen e kushteve të Cauchy-Riemann:

Shembulli 9

Përcaktoni pjesët reale dhe imagjinare të një funksioni . Kontrolloni përmbushjen e kushteve të Cauchy-Riemann. Kështu qoftë, ne nuk do ta gjejmë derivatin.

Zgjidhja: Algoritmi i zgjidhjes është shumë i ngjashëm me dy shembujt e mëparshëm, por ka pika shumë të rëndësishme, kështu që unë do të komentoj përsëri hap pas hapi fazën fillestare:

Që atëherë:

1) Ne zëvendësojmë në vend të "z".

(2) Së pari, zgjidhni pjesët reale dhe imagjinare brenda sinusit. Për këtë qëllim, hapni kllapat.

(3) Ne përdorim formulën , ndërsa .

(4) Përdorimi barazia e kosinusit hiperbolik: dhe çuditshmëria hiperbolike e sinusit: . Hiperbolikët, megjithëse nuk janë të kësaj bote, por në shumë mënyra ngjajnë me funksione të ngjashme trigonometrike.

Përfundimisht:
është pjesa reale e funksionit;
është pjesa imagjinare e funksionit .

Kujdes! Shenja minus i referohet pjesës imagjinare dhe në asnjë rast nuk duhet ta humbasim atë! Për një ilustrim vizual, rezultati i marrë më sipër mund të rishkruhet si më poshtë:

Le të kontrollojmë përmbushjen e kushteve Cauchy-Riemann:

Kushtet Cauchy-Riemann janë përmbushur.

Përgjigje:, , kushtet Cauchy-Riemann janë të kënaqur.

Me kosinus, zonja dhe zotërinj, ne e kuptojmë vetë:

Shembulli 10

Përcaktoni pjesët reale dhe imagjinare të funksionit. Kontrolloni përmbushjen e kushteve të Cauchy-Riemann.

Kam marrë qëllimisht shembuj më të ndërlikuar, sepse të gjithë mund të trajtojnë diçka si kikirikë të qëruar. Në të njëjtën kohë, stërvitni vëmendjen tuaj! Arrëthyesi në fund të mësimit.

Epo, në përfundim, unë do të shqyrtoj një shembull tjetër interesant kur argumenti kompleks është në emërues. Ne u takuam nja dy herë në praktikë, le të analizojmë diçka të thjeshtë. Oh po plakem...

Shembulli 11

Përcaktoni pjesët reale dhe imagjinare të funksionit. Kontrolloni përmbushjen e kushteve të Cauchy-Riemann.

Zgjidhja: Përsëri, është e nevojshme të ndahen pjesët reale dhe imagjinare të funksionit.
Nese atehere

Shtrohet pyetja, çfarë të bëjmë kur "Z" është në emërues?

Gjithçka është e thjeshtë - standardi do të ndihmojë metoda e shumëzimit të numëruesit dhe emëruesit me shprehjen e konjuguar, tashmë është përdorur në shembujt e mësimit Numrat kompleksë për dummies. Le të kujtojmë formulën e shkollës. Në emëruesin që kemi tashmë, kështu shprehja e konjuguar do të jetë . Kështu, ju duhet të shumëzoni numëruesin dhe emëruesin me:

11 Funksionet themelore të një ndryshoreje komplekse

Kujtoni përkufizimin e eksponentit kompleks - . Pastaj

Zgjerimi i serisë Maclaurin. Rrezja e konvergjencës së kësaj serie është +∞, që do të thotë se eksponenti kompleks është analitik në të gjithë planin kompleks dhe

(exp z)"=exp z; exp 0=1. (2)

Barazia e parë këtu vjen, për shembull, nga teorema mbi diferencimin term pas termi të një serie fuqie.

11.1 Funksionet trigonometrike dhe hiperbolike

Sinusi i një ndryshoreje komplekse quhet funksion

Kosinusi i një ndryshoreje komplekse ka një funksion

Sinusi hiperbolik i një ndryshoreje komplekse përkufizohet kështu:

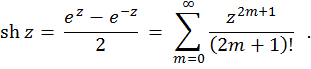
Kosinusi hiperbolik i një ndryshoreje komplekse-- është një funksion

Vëmë re disa veti të funksioneve të prezantuara rishtazi.

A. Nëse x∈ ℝ , atëherë cos x, sin x, ch x, sh x∈ ℝ .

B. Ekziston lidhja e mëposhtme midis funksioneve trigonometrike dhe hiperbolike:

cos iz=ch z; sin iz=ish z, ch iz=cos z; shiz=isinz.

B. Identitete bazë trigonometrike dhe hiperbolike:

cos 2 z+sin 2 z=1; ch 2 z-sh 2 z=1.

Vërtetim i identitetit bazë hiperbolik.

Identiteti kryesor trigonometrik rrjedh nga identiteti hiperbolik Ononian kur merret parasysh lidhja midis funksioneve trigonometrike dhe hiperbolike (shih vetinë B)

G Formulat e shtimit:

Veçanërisht,

D. Për të llogaritur derivatet e funksioneve trigonometrike dhe hiperbolike, duhet zbatuar teorema e diferencimit term pas termi të një serie fuqie. Ne marrim:

(cos z)"=-sin z; (sin z)"=cos z; (ch z)"=sh z; (sh z)"=ch z.

E. Funksionet cos z, ch z janë çift, ndërsa funksionet sin z, sh z janë tek.

G. (Periodiciteti) Funksioni e z është periodik me periodë 2π i. Funksionet cos z, sin z janë periodikë me periodë 2π, dhe funksionet ch z, sh z janë periodike me periodë 2πi. Për më tepër,

Duke zbatuar formulat e shumës, marrim

W. Zbërthen në pjesë reale dhe imagjinare:

Nëse një funksion analitik me një vlerë të vetme f(z) harton në mënyrë bijektive një domen D në një domen G, atëherë D quhet një domen i njëvalencës.

DHE. Domeni D k =( x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .

Dëshmi. Lidhja (5) nënkupton që pasqyrimi exp:D k → ℂ është injektiv. Le të jetë w çdo numër kompleks jozero. Pastaj, zgjidhja e ekuacioneve e x =|w| dhe e iy =w/|w| me ndryshoret reale x dhe y (ne zgjedhim y nga gjysma e intervalit)