निर्धारक गुण। निर्धारक के क्रम को कम करना

कुछ संख्याएक निश्चित नियम के अनुसार गणना की जाती है और कहा जाता है सिद्ध.

अवधारणा को पेश करने की आवश्यकता सिद्ध - संख्यानिस्र्पक वर्गआदेश मैट्रिक्स एन , रैखिक बीजीय समीकरणों की प्रणालियों के समाधान से निकटता से संबंधित है।

एक मैट्रिक्स का निर्धारक एहम निरूपित करेंगे: | ए| या डी.

प्रथम-क्रम मैट्रिक्स का निर्धारकए = (ए 11) एक तत्व कहा जाता है एग्यारह । उदाहरण के लिए, के लिए ए= (-4) हमारे पास | ए| = -4.

दूसरे क्रम के मैट्रिक्स का निर्धारकबुलाया संख्यासूत्र द्वारा निर्धारित

|ए| = .

उदाहरण के लिए | ए| = .

शब्दों में, इस नियम को इस प्रकार लिखा जा सकता है: अपने स्वयं के संकेत के साथ आपको जुड़े हुए तत्वों का उत्पाद लेने की आवश्यकता है मुख्य विकर्ण, और त्रिभुजों के शीर्षों से जुड़े तत्वों के गुणनफल, जिसके लिए मुख्य विकर्ण के समानांतर आधार... विपरीत चिन्ह के साथ, हम समान उत्पाद लेते हैं, केवल पार्श्व विकर्ण के संबंध में।

उदाहरण के लिए,

मैट्रिक्स के निर्धारक का निर्धारण एनहम वां क्रम नहीं देंगे, लेकिन केवल इसे खोजने की विधि दिखाएंगे।

इसके अलावा, शब्दों के बजाय एक मैट्रिक्स का निर्धारक एन-वें क्रमयूही ही कहते हैं सिद्ध एन-वें क्रम... आइए नई अवधारणाओं का परिचय दें।

एक वर्ग मैट्रिक्स दिया गया एनवें आदेश।

अवयस्कएम ij तत्व ए ij मैट्रिसेस एबुलाया सिद्ध (एन-1) मैट्रिक्स से प्राप्त वां क्रम एहटाने मैं-वीं पंक्ति और जेवें स्तंभ।

मैट्रिक्स के तत्व а ij के बीजगणितीय पूरक ij को इसका नाबालिग कहा जाता है, जिसे चिह्न (-1) i + j के साथ लिया जाता है:

ए ij = (-1) मैं + जे एमआईजे,

वे। एक बीजीय पूरक या तो अपने नाबालिग के साथ मेल खाता है जब पंक्ति और स्तंभ संख्याओं का योग एक सम संख्या होती है, या जब पंक्ति और स्तंभ संख्याओं का योग एक विषम संख्या होती है, तो इससे भिन्न होता है।

उदाहरण के लिए, तत्वों के लिए ए११ और ए 12 आव्यूह ए = नाबालिगों

एम 11 = ए 11 = ,

एम 12 = ,

ए ए 12 = (-1) 1+2 एम 12 = -8.

प्रमेय (निर्धारक के विस्तार पर) . एक वर्ग मैट्रिक्स का निर्धारक किसी भी पंक्ति (स्तंभ) के तत्वों के उत्पादों के योग के बराबर होता है, उनके बीजगणितीय पूरक, यानी।

|ए| = ए i1 ए i1 + ए i2 ए i2 + ... + एमें एमें,
किसी के लिए भी मैं = 1, 2, …, एन

|ए| = ए 1जे ए 1j + ए 2जे ए 2j + ... + एन्यू जर्सी एएनजे,

किसी के लिए भी जे = 1, 2, …, एन

पहला सूत्र कहा जाता है मैं-वीं पंक्ति,और दूसरा है तत्वों में सारणिक का विस्तार जेवें स्तंभ।

यह समझना आसान है कि इन सूत्रों की सहायता से कोई भी निर्धारक एन-वें क्रम को निर्धारकों के योग तक घटाया जा सकता है, जिसका क्रम 1 कम होगा, आदि। जब तक हम तीसरे या दूसरे क्रम के निर्धारकों तक नहीं पहुंच जाते, जिसकी गणना अब मुश्किल नहीं है।

निर्धारक को खोजने के लिए, निम्नलिखित मूल गुणों को लागू किया जा सकता है:

1. यदि सारणिक की किसी पंक्ति (या स्तंभ) में शून्य है, तो सारणिक स्वयं शून्य के बराबर है।

2. किन्हीं दो पंक्तियों (या दो स्तंभों) की अदला-बदली करते समय, सारणिक को -1 से गुणा किया जाता है।

3. दो समान या आनुपातिक पंक्तियों (या स्तंभों) के साथ सारणिक शून्य के बराबर है।

4. सारणिक चिह्न से किसी भी पंक्ति (या स्तंभ) के तत्वों का उभयनिष्ठ गुणनखंड निकाला जा सकता है।

5. यदि सभी पंक्तियों और स्तंभों की अदला-बदली की जाती है, तो निर्धारक का मान नहीं बदलेगा।

6. सारणिक का मान नहीं बदलेगा यदि किसी अन्य पंक्ति (स्तंभ) को किसी संख्या से गुणा करने पर पंक्तियों में से एक (या किसी एक स्तंभ में) जोड़ दिया जाए।

7. इस मैट्रिक्स की दूसरी पंक्ति (स्तंभ) के तत्वों के बीजगणितीय पूरक द्वारा मैट्रिक्स की किसी पंक्ति (या स्तंभ) के तत्वों के उत्पादों का योग शून्य के बराबर होता है।

8. दो वर्ग आव्यूहों के गुणनफल का सारणिक उनके सारणिकों के गुणनफल के बराबर होता है।

एक मैट्रिक्स के निर्धारक की धारणा का परिचय हमें मैट्रिक्स के साथ एक और क्रिया को परिभाषित करने की अनुमति देता है - उलटा मैट्रिक्स ढूंढना।

प्रत्येक अशून्य संख्या के लिए एक व्युत्क्रम संख्या होती है जिससे इन संख्याओं का गुणनफल एक देता है। स्क्वायर मैट्रिसेस के लिए भी ऐसी ही एक अवधारणा है।

आव्यूह ए-1 कहा जाता है उलटनाकी ओर वर्गआव्यूह एयदि इस आव्यूह को दायीं और बायीं ओर दिए गए मैट्रिक्स से गुणा करने पर प्राप्त होता है पहचान मैट्रिक्स, अर्थात।

ए× ए -1 = ए-1 × ए= इ।

यह परिभाषा से इस प्रकार है कि केवल एक वर्ग मैट्रिक्स में एक व्युत्क्रम होता है; इस मामले में, व्युत्क्रम मैट्रिक्स उसी क्रम का वर्ग होगा। हालांकि, हर वर्ग मैट्रिक्स का अपना व्युत्क्रम नहीं होता है।

बीजीय पूरक और अवयस्क

आइए तीसरे क्रम का एक निर्धारक प्राप्त करें: .

अवयस्कइस तत्व के अनुरूप एक आईजूतीसरे क्रम के निर्धारक को दूसरे क्रम का सारणिक कहा जाता है, जो दिए गए तत्व के चौराहे पर पंक्ति और स्तंभ को हटाकर प्राप्त किया जाता है, अर्थात। मैं-वीं पंक्ति और जेवें स्तंभ। किसी दिए गए तत्व के अनुरूप नाबालिग एक आईजूनिरूपित करेंगे एम आईजो.

उदाहरण के लिए, अवयस्क एम 12तत्व के अनुरूप एक 12, एक निर्धारक होगा 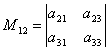, जो दिए गए सारणिक से पहली पंक्ति और दूसरे स्तंभ को हटाकर प्राप्त किया जाता है।

इस प्रकार, तीसरे क्रम के निर्धारक को परिभाषित करने वाला सूत्र दर्शाता है कि यह निर्धारक संबंधित नाबालिगों द्वारा पहली पंक्ति के तत्वों के उत्पादों के योग के बराबर है; इस मामले में, तत्व के अनुरूप नाबालिग एक 12, "-" चिन्ह के साथ लिया गया, अर्थात। हम लिख सकते हैं कि

इसी तरह, हम दूसरे क्रम और उच्च क्रम के निर्धारकों के लिए नाबालिगों की परिभाषा पेश कर सकते हैं।

आइए एक और अवधारणा का परिचय दें।

बीजीय पूरकतत्त्व एक आईजूनिर्धारक को इसका नाबालिग कहा जाता है एम आईजो(-1) i + j से गुणा किया जाता है।

एक तत्व का बीजीय पूरक एक आईजूलक्षित एक इजी.

परिभाषा से हम प्राप्त करते हैं कि एक तत्व के बीजीय पूरक और उसके नाबालिग के बीच संबंध समानता द्वारा व्यक्त किया जाता है एक इजी= (-1) मैं + जे एम आई.जी.

उदाहरण के लिए,

उदाहरण।एक निर्धारक दिया गया है। पाना ए 13, ए 21, ए 32.

यह देखना आसान है कि तत्वों के बीजीय पूरक का उपयोग करके सूत्र (1) को इस रूप में लिखा जा सकता है:

इसी तरह इस सूत्र के लिए, आप किसी भी पंक्ति या स्तंभ के तत्वों में सारणिक का अपघटन प्राप्त कर सकते हैं।

उदाहरण के लिए, दूसरी पंक्ति के तत्वों द्वारा निर्धारक का गुणन निम्नानुसार प्राप्त किया जा सकता है। सारणिक की संपत्ति 2 के अनुसार, हमारे पास है:

आइए हम पहली पंक्ति के तत्वों द्वारा परिणामी निर्धारक का विस्तार करें।

.

(2)

यहाँ से जबसे सूत्र (2) में दूसरे क्रम के निर्धारक तत्वों के अवयस्क हैं एक 21, एक 22, एक 23... इस प्रकार, अर्थात्। हमें दूसरी पंक्ति के तत्वों के संदर्भ में सारणिक का अपघटन मिला।

इसी तरह, आप तीसरी पंक्ति के तत्वों के संदर्भ में सारणिक का गुणनखंडन प्राप्त कर सकते हैं। निर्धारकों के गुण 1 (स्थानांतरण के बारे में) का उपयोग करके, कोई यह दिखा सकता है कि स्तंभ तत्वों के संदर्भ में समान विस्तार भी विस्तार के लिए मान्य हैं।

इस प्रकार, निम्नलिखित प्रमेय सत्य है।

प्रमेय (किसी दी गई पंक्ति या स्तंभ में एक सारणिक के विस्तार पर)।सारणिक अपनी किसी भी पंक्ति (या स्तंभ) के तत्वों के गुणनफल के योग के बराबर होता है, जो उनके बीजीय संपूरकों द्वारा होता है।

उपरोक्त सभी किसी भी उच्च क्रम के निर्धारकों के लिए भी सही हैं।

उदाहरण।

उलटा मैट्रिक्स

व्युत्क्रम मैट्रिक्स की अवधारणा केवल के लिए प्रस्तुत की गई है वर्ग मैट्रिसेस.

अगर एएक वर्ग मैट्रिक्स है, तो उलटनाइसके लिए, एक मैट्रिक्स को मैट्रिक्स कहा जाता है, जिसे निरूपित किया जाता है ए -1और स्थिति को संतुष्ट करना। (यह परिभाषा संख्याओं के गुणन के साथ सादृश्य द्वारा प्रस्तुत की गई है)

संपत्ति 1. सारणिक का मान नहीं बदलेगा यदि उसकी सभी पंक्तियों को स्तंभों से बदल दिया जाता है, और प्रत्येक पंक्ति को समान संख्या वाले स्तंभ द्वारा प्रतिस्थापित किया जाता है, अर्थात

संपत्ति 2. एक सारणिक के दो स्तंभों या दो पंक्तियों का क्रमपरिवर्तन इसे -1 से गुणा करने के बराबर है। उदाहरण के लिए,

.

संपत्ति 3. यदि सारणिक में दो समान स्तंभ या दो समान पंक्तियाँ हैं, तो यह शून्य के बराबर है।

गुण 4. सारणिक के एक स्तंभ या एक पंक्ति के सभी तत्वों का किसी भी संख्या k से गुणा करना, सारणिक को इस संख्या k से गुणा करने के बराबर है। उदाहरण के लिए,

.

गुण 5. यदि किसी स्तंभ या किसी पंक्ति के सभी अवयव शून्य के बराबर हों, तो सारणिक स्वयं शून्य के बराबर होता है. यह गुण पिछले वाले का एक विशेष मामला है (k = 0 के लिए)।

गुण 6. यदि सारणिक के दो स्तंभों या दो पंक्तियों के संगत तत्व समानुपाती हों, तो सारणिक शून्य के बराबर होता है।

संपत्ति 7. यदि सारणिक के n-वें स्तंभ या n-वें पंक्ति का प्रत्येक तत्व दो पदों का योग है, तो सारणिक को दो निर्धारकों के योग के रूप में दर्शाया जा सकता है, जिनमें से एक n-वें स्तंभ में या , क्रमशः, n-वें पंक्ति में उल्लिखित पदों में से पहला है, और दूसरा - दूसरा; शेष स्थानों के तत्व तीन निर्धारकों के मील के पत्थर के लिए समान हैं। उदाहरण के लिए,

संपत्ति 8. यदि किसी स्तंभ (या कुछ पंक्ति) के तत्वों में हम किसी अन्य स्तंभ (या दूसरी पंक्ति) के संगत तत्वों को किसी सामान्य गुणनखंड से गुणा करते हैं, तो सारणिक का मान नहीं बदलेगा। उदाहरण के लिए,

.

निर्धारकों के आगे के गुण बीजगणितीय पूरक और नाबालिग की अवधारणा से संबंधित हैं। किसी तत्व का अवयस्क वह सारणिक होता है, जिसके चौराहे पर यह तत्व स्थित होता है, उस पंक्ति और स्तंभ को हटाकर दिए गए से प्राप्त किया जाता है।

निर्धारक के किसी भी तत्व का बीजगणितीय पूरक इस तत्व के नाबालिग के बराबर होता है, अपने स्वयं के चिन्ह से लिया जाता है, यदि उस चौराहे पर पंक्ति और स्तंभ की संख्याओं का योग एक सम संख्या है, और विपरीत चिन्ह के साथ यदि यह संख्या विषम है।

हम एक तत्व के बीजगणितीय पूरक को उसी नाम के एक बड़े अक्षर और उसी संख्या के रूप में निरूपित करेंगे जो तत्व को स्वयं निर्दिष्ट करता है।

संपत्ति 9. निर्धारक

किसी भी स्तंभ (या पंक्ति) के तत्वों के गुणनफल के योग के बराबर है, उनके बीजीय पूरक द्वारा।

दूसरे शब्दों में, निम्नलिखित समानताएँ धारण करती हैं:

, ,

, .

6) नाबालिग और बीजीय जोड़।

परिभाषा। सारणिक का लघु अवयव है गणकहा जाता है सिद्ध- वें क्रम, जो दिए गए से प्राप्त होता है सिद्ध-वें पंक्ति और -वें स्तंभ को पार करके जिस चौराहे पर तत्व खड़ा है।

पद:।

परिभाषा। क्रम के निर्धारक के एक तत्व के बीजगणितीय पूरक को इसका नाबालिग कहा जाता है, यदि यह एक सम संख्या है और ऋण चिह्न के साथ अन्यथा प्लस चिह्न के साथ लिया जाता है।

पद:।

प्रमेय। (निर्धारक के विस्तार पर।)

सारणिक, सारणिक की किसी भी पंक्ति (या किसी स्तंभ) के तत्वों के गुणनफल के योग के बराबर होता है, जो उनके बीजीय संपूरकों द्वारा होता है:

7) उलटा मैट्रिक्स- ऐसा आव्यूह ए −1 , जब से गुणा किया जाता है, तो मूल मैट्रिक्स एका परिणाम पहचान मैट्रिक्स इ:

स्क्वायर मैट्रिक्सप्रतिवर्ती है यदि और केवल यदि यह गैर-अपक्षयी है, अर्थात इसका सिद्धशून्य नहीं है। गैर-वर्ग मैट्रिक्स के लिए और पतित मैट्रिसेसकोई व्युत्क्रम मैट्रिक्स नहीं हैं। हालाँकि, इस अवधारणा को सामान्य बनाना और परिचय देना संभव है स्यूडोइनवर्स मैट्रिसेस, कई गुणों में व्युत्क्रम के समान।

8)मैट्रिक्स रैंक- उच्चतम आदेश नाबालिगोंइस गैर-शून्य मैट्रिक्स का

आमतौर पर एक मैट्रिक्स की रैंक () या द्वारा निरूपित की जाती है। दोनों पदनाम विदेशी भाषाओं से हमारे पास आए, इसलिए दोनों का उपयोग किया जा सकता है।

गुण

प्रमेय (मूल अवयस्क पर): मान लीजिए r = rang A M आव्यूह A का मूल अवयस्क है, तब:

आधार पंक्तियाँ और आधार स्तंभ रैखिक रूप से स्वतंत्र हैं;

मैट्रिक्स A की कोई भी पंक्ति (स्तंभ) मूल पंक्तियों (स्तंभों) का एक रैखिक संयोजन है।

- निश्चित मौत के लिए शीर्षक जारी करें!
स्वतंत्रता उसे दुलार दो!
और जहाज चलता है, और रिएक्टर दहाड़ता है ...
- पश, क्या तुम खराब हो गए हो?

मुझे याद है कि आठवीं कक्षा से पहले मुझे बीजगणित पसंद नहीं था। मुझे यह बिल्कुल पसंद नहीं आया। उसने मुझे चिढ़ाया। क्योंकि मुझे वहां कुछ समझ नहीं आया।

और फिर सब कुछ बदल गया, क्योंकि मैं एक टुकड़े से गुज़रा:

सामान्य रूप से गणित में (और विशेष रूप से बीजगणित), सब कुछ परिभाषाओं की एक सक्षम और सुसंगत प्रणाली पर बनाया गया है। आप परिभाषाएँ जानते हैं, आप उनका सार समझते हैं - बाकी का पता लगाना मुश्किल नहीं होगा।

तो यह आज के पाठ के विषय के साथ है। हम कई संबंधित मुद्दों और परिभाषाओं पर विस्तार से विचार करेंगे, जिसके लिए आप एक बार और सभी के लिए मैट्रिसेस, और निर्धारकों के साथ, और उनके सभी गुणों से निपटेंगे।

मैट्रिक्स बीजगणित में निर्धारक एक केंद्रीय अवधारणा हैं। संक्षिप्त गुणन फ़ार्मुलों की तरह, वे आपके उन्नत गणित पाठ्यक्रम के दौरान आपको परेशान करेंगे। इसलिए, हम अच्छी तरह से पढ़ते हैं, देखते हैं और समझते हैं। :)

और हम सबसे अंतरंग से शुरू करेंगे - मैट्रिक्स क्या है? और इसके साथ सही तरीके से कैसे काम करें।

मैट्रिक्स में सूचकांकों का सही स्थान

एक मैट्रिक्स सिर्फ संख्याओं से भरी एक तालिका है। नियो का इससे कोई लेना-देना नहीं है।

मैट्रिक्स की प्रमुख विशेषताओं में से एक इसका आयाम है, अर्थात। इसमें शामिल पंक्तियों और स्तंभों की संख्या। आमतौर पर यह कहा जाता है कि कुछ मैट्रिक्स $ A $ का आकार $ \ बाएँ [m \ बार n \ दाएँ] $ होता है यदि इसमें $ m $ पंक्तियाँ और $ n $ कॉलम हों। वे इसे इस प्रकार लिखते हैं:

या इस तरह:

अन्य पदनाम हैं - यह सब व्याख्याता / संगोष्ठी / पाठ्यपुस्तक के लेखक की प्राथमिकताओं पर निर्भर करता है। लेकिन किसी भी स्थिति में, इन सभी $ \ बाएँ [m \ बार n \ दाएँ] $ और $ ((a) _ (ij)) $ के साथ, वही समस्या होती है:

कौन सा सूचकांक किसके लिए जिम्मेदार है? पहले पंक्ति संख्या है, फिर स्तंभ? या ठीक इसके विपरीत?

व्याख्यान और पाठ्यपुस्तकों को पढ़ते समय, उत्तर स्पष्ट प्रतीत होगा। लेकिन जब परीक्षा में आपके सामने केवल एक समस्या का पत्रक होता है, तो आप अभिभूत हो सकते हैं और अचानक भ्रमित हो सकते हैं।

तो आइए इस मुद्दे से हमेशा के लिए निपटें। आरंभ करने के लिए, आइए स्कूल गणित पाठ्यक्रम से सामान्य समन्वय प्रणाली को याद करें:

एक विमान पर एक समन्वय प्रणाली का परिचय

उसे याद है? इसका मूल (बिंदु $ O = \ बाएँ (0; 0 \ दाएँ) $) अक्ष $ x $ और $ y $ है, और विमान पर प्रत्येक बिंदु निर्देशांक द्वारा विशिष्ट रूप से निर्धारित किया जाता है: $ A = \ बाएँ (1; 2 \ दाएँ) $, $ B = \ बाएँ (3; 1 \ दाएँ) $, आदि।

अब इस निर्माण को लेते हैं और इसे मैट्रिक्स के बगल में रखते हैं ताकि मूल ऊपरी बाएँ कोने में हो। वहाँ क्यों? क्योंकि जब हम कोई किताब खोलते हैं, तो हम पृष्ठ के ऊपरी बाएँ कोने से पढ़ना शुरू करते हैं - इसे याद रखना आसान होता है।

लेकिन कुल्हाड़ियों को कहाँ निर्देशित किया जाना चाहिए? हम उन्हें निर्देशित करेंगे ताकि हमारा पूरा वर्चुअल "पेज" इन अक्षों से ढका हो। सच है, इसके लिए आपको हमारे समन्वय प्रणाली को घुमाना होगा। ऐसी व्यवस्था के लिए एकमात्र संभव विकल्प:

अब मैट्रिक्स के प्रत्येक सेल में एकल-मूल्यवान निर्देशांक $ x $ और $ y $ हैं। उदाहरण के लिए, रिकॉर्ड $ ((a) _ (24)) $ का अर्थ है कि हम निर्देशांक $ x = 2 $ और $ y = 4 $ वाले तत्व की बात कर रहे हैं। मैट्रिक्स के आयाम भी विशिष्ट रूप से संख्याओं की एक जोड़ी द्वारा निर्धारित किए जाते हैं:

जरा गौर से देखिए इस तस्वीर को। निर्देशांक के साथ खेलें (विशेषकर जब आप वास्तविक मैट्रिक्स और निर्धारकों के साथ काम करते हैं) - और बहुत जल्द आप महसूस करेंगे कि सबसे जटिल प्रमेयों और परिभाषाओं में भी, आप पूरी तरह से समझते हैं कि क्या दांव पर है।

समझा? खैर, आइए ज्ञानोदय के पहले चरण पर चलते हैं - निर्धारक की ज्यामितीय परिभाषा। :)

ज्यामितीय परिभाषा

सबसे पहले, मैं यह नोट करना चाहूंगा कि निर्धारक केवल फॉर्म के वर्ग मैट्रिक्स के लिए मौजूद है $ \ left [n \ times n \ right] $। एक निर्धारक एक संख्या है जिसकी गणना कुछ नियमों के अनुसार की जाती है और यह इस मैट्रिक्स की विशेषताओं में से एक है (अन्य विशेषताएं हैं: रैंक, eigenvectors, लेकिन अन्य पाठों में उस पर अधिक)।

तो यह विशेषता क्या है? इसका क्या मतलब है? यह आसान है:

एक वर्ग मैट्रिक्स का निर्धारक $ A = \ बाएँ [n \ बार n \ दाएँ] $ एक $ n $ -आयामी समानांतर चतुर्भुज का आयतन है, जो तब बनता है जब हम मैट्रिक्स की पंक्तियों को इसके किनारों को बनाने वाले वैक्टर के रूप में मानते हैं समानांतर चतुर्भुज।

उदाहरण के लिए, 2x2 मैट्रिक्स का निर्धारक केवल समांतर चतुर्भुज का क्षेत्र है, और 3x3 मैट्रिक्स के लिए यह पहले से ही 3-आयामी समानांतर चतुर्भुज का आयतन है - वह जो सभी हाई स्कूल के छात्रों को स्टीरियोमेट्री पाठों में प्रभावित करता है।

पहली नज़र में, यह परिभाषा पूरी तरह से अपर्याप्त लग सकती है। लेकिन आइए निष्कर्ष पर न जाएं - आइए उदाहरणों को देखें। वास्तव में, सब कुछ प्राथमिक है, वाटसन:

कार्य। मैट्रिक्स के निर्धारक खोजें:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 1 और 0 \\ 0 और 3 \\\ अंत (मैट्रिक्स) \ दाएँ | \ क्वाड \ बाएँ | \ शुरू (मैट्रिक्स) 1 और -1 \\ 2 और 2 \\\ अंत (मैट्रिक्स) \ दाएँ | \ क्वाड \ बाएँ | \ शुरू (मैट्रिक्स) 2 और 0 और 0 \\ 1 और 3 और 0 \\ 1 और 1 और 4 \\\ अंत (मैट्रिक्स) \ दाएं | \]

समाधान। पहले दो क्वालिफायर 2x2 हैं। तो ये केवल समांतर चतुर्भुजों के क्षेत्रफल हैं। आइए उन्हें ड्रा करें और क्षेत्र की गणना करें।

पहला समांतर चतुर्भुज वैक्टर $ ((v) _ (1)) = \ बाएँ (1; 0 \ दाएँ) $ और $ ((v) _ (2)) = \ बाएँ (0; 3 \ दाएँ) पर बनाया गया है $:

सारणिक 2x2 समांतर चतुर्भुज का क्षेत्रफल है

जाहिर है, यह सिर्फ एक समांतर चतुर्भुज नहीं है, बल्कि काफी आयत है। इसका क्षेत्रफल है

दूसरा समांतर चतुर्भुज वैक्टर $ ((v) _ (1)) = \ बाएँ (1; -1 \ दाएँ) $ और $ ((v) _ (2)) = \ बाएँ (2; 2 \ दाएँ) पर बनाया गया है ) $. अच्छा, तो क्या? यह भी एक आयत है:

एक अन्य निर्धारक 2x2

इस आयत की भुजाएँ (वास्तव में, सदिशों की लंबाई) पाइथागोरस प्रमेय द्वारा आसानी से परिकलित की जाती हैं:

\ [\ प्रारंभ (संरेखित करें) और \ बाएँ | ((v) _ (1)) \ दाएँ | = \ sqrt (((1) ^ (2)) + ((\ बाएँ (-1 \ दाएँ)) ^ (2))) = \ sqrt (2); \\ और \ बाएं | ((v) _ (2)) \ दाएँ | = \ sqrt (((2) ^ (2)) + ((2) ^ (2))) = \ sqrt (8) = 2 \ sqrt (2); \\ और एस = \ बाएं | ((v) _ (1)) \ दाएँ | \ cdot \ बाएँ | ((v) _ (2)) \ दाएँ | = \ sqrt (2) \ cdot 2 \ sqrt (2) = 4। \\\ अंत (संरेखित करें) \]

यह अंतिम निर्धारक से निपटने के लिए बनी हुई है - पहले से ही एक 3x3 मैट्रिक्स है। हमें स्टीरियोमेट्री याद रखनी होगी:

सारणिक 3x3 समांतर चतुर्भुज का आयतन है

यह मस्तिष्क को अवशोषित करने वाला लगता है, लेकिन वास्तव में यह एक समानांतर चतुर्भुज के आयतन के सूत्र को याद करने के लिए पर्याप्त है:

जहां $ S $ आधार का क्षेत्र है (हमारे मामले में, यह $ OXY $ विमान पर समांतर चतुर्भुज का क्षेत्र है), $ h $ इस आधार पर खींची गई ऊंचाई है (वास्तव में, $ z $ -सदिश $ ((v) _ (3)) $) का निर्देशांक।

समांतर चतुर्भुज का क्षेत्रफल (हमने इसे अलग से खींचा है) भी गणना करना आसान है:

\ [\ शुरू (संरेखित करें) और एस = 2 \ cdot 3 = 6; \\ और वी = एस \ cdot h = 6 \ cdot 4 = 24। \\\ अंत (संरेखित करें) \]

बस इतना ही! हम उत्तर लिखते हैं।

उत्तर: ३; 4; 24.

नोटेशन सिस्टम पर एक त्वरित नोट। किसी को शायद यह पसंद नहीं होगा कि मैं वैक्टर के ऊपर "तीर" को अनदेखा करता हूं। कथित तौर पर, इस तरह आप एक वेक्टर को एक बिंदु या कुछ और से भ्रमित कर सकते हैं।

लेकिन आइए गंभीर हों: आप और मैं पहले से ही बड़े हो चुके लड़के और लड़कियां हैं, इसलिए संदर्भ से हम पूरी तरह से समझते हैं कि जब एक वेक्टर की बात आती है, और कब एक बिंदु पर। तीर केवल कहानी को कूड़ा देता है, जो पहले से ही गणितीय सूत्रों से भरा हुआ है।

और आगे। सिद्धांत रूप में, कुछ भी हमें 1x1 मैट्रिक्स के निर्धारक पर विचार करने से नहीं रोकता है - ऐसा मैट्रिक्स सिर्फ एक सेल है, और इस सेल में लिखी गई संख्या निर्धारक होगी। लेकिन यहाँ एक महत्वपूर्ण नोट है:

शास्त्रीय मात्रा के विपरीत, निर्धारक हमें तथाकथित " उन्मुख मात्रा", अर्थात। मात्रा, पंक्ति वैक्टर के विचार के क्रम को ध्यान में रखते हुए।

और यदि आप शब्द के शास्त्रीय अर्थ में वॉल्यूम प्राप्त करना चाहते हैं, तो आपको निर्धारक मॉड्यूल लेना होगा, लेकिन अब आपको इसके बारे में चिंता नहीं करनी चाहिए - वैसे भी, कुछ सेकंड में हम किसी भी सारणिक को किसी भी संकेत के साथ गिनना सीखेंगे , आकार, आदि :)

बीजीय परिभाषा

ज्यामितीय दृष्टिकोण की सभी सुंदरता और स्पष्टता के लिए, इसमें एक गंभीर खामी है: यह हमें इस बारे में कुछ भी नहीं बताता है कि इस बहुत ही निर्धारक की गणना कैसे की जाए।

इसलिए, अब हम एक वैकल्पिक परिभाषा का विश्लेषण करेंगे - बीजीय। ऐसा करने के लिए, हमें एक संक्षिप्त सैद्धांतिक तैयारी की आवश्यकता है, लेकिन अंत में हमें एक उपकरण मिलेगा जो हमें मैट्रिक्स में कुछ भी गिनने की अनुमति देता है और हम कैसे चाहते हैं।

सच है, एक नई समस्या होगी ... लेकिन पहले चीज़ें पहले।

क्रमपरिवर्तन और व्युत्क्रम

आइए 1 से $ n $ तक की संख्याओं को एक पंक्ति में लिखें। आप इस तरह कुछ खत्म करते हैं:

अब (विशुद्ध रूप से मनोरंजन के लिए) आइए कुछ नंबरों की अदला-बदली करें। आप आसन्न लोगों को बदल सकते हैं:

या आप कर सकते हैं - बहुत पड़ोसी नहीं:

और क्या आपको पता है? लेकिन कुछ नहीं! बीजगणित में, इस बकवास को क्रमपरिवर्तन कहा जाता है। और उसके पास गुणों का एक गुच्छा है।

परिभाषा। लंबाई $ n $ का क्रमपरिवर्तन $ n $ विशिष्ट संख्याओं की एक स्ट्रिंग है, जिसे किसी भी क्रम में लिखा जाता है। आमतौर पर, पहले $ n $ प्राकृतिक संख्याओं पर विचार किया जाता है (अर्थात, केवल संख्या 1, 2, ..., $ n $), और फिर उन्हें वांछित क्रमपरिवर्तन प्राप्त करने के लिए मिलाया जाता है।

क्रमपरिवर्तन को उसी तरह से निरूपित किया जाता है जैसे वैक्टर - सिर्फ एक अक्षर और कोष्ठक में उनके तत्वों की एक क्रमिक सूची। उदाहरण के लिए: $ p = \ बाएँ (1; 3; 2 \ दाएँ) $ या $ p = \ बाएँ (2; 5; 1; 4; 3 \ दाएँ) $। पत्र कुछ भी हो सकता है, लेकिन इसे $p$ होने दें। :)

इसके अलावा, सादगी के लिए, हम लंबाई 5 के क्रमपरिवर्तन के साथ काम करेंगे - वे पहले से ही किसी भी संदिग्ध प्रभाव का निरीक्षण करने के लिए पर्याप्त गंभीर हैं, लेकिन अभी तक एक अपरिपक्व मस्तिष्क के लिए लंबाई 6 या उससे अधिक के क्रमपरिवर्तन के रूप में गंभीर नहीं हैं। ऐसे क्रमपरिवर्तन के उदाहरण यहां दिए गए हैं:

\ [\ प्रारंभ (संरेखित करें) और ((पी) _ (1)) = \ बाएँ (1; 2; 3; 4; 5 \ दाएँ) \\ & ((p) _ (2)) = \ बाएँ (1 ; 3; 2; 5; 4 \ दाएँ) \\ & ((पी) _ (3)) = \ बाएँ (5; 4; 3; 2; 1 \ दाएँ) \\\ अंत (संरेखित) \]

स्वाभाविक रूप से, लंबाई $ n $ के क्रमपरिवर्तन को एक फ़ंक्शन के रूप में माना जा सकता है जिसे सेट $ \ बाएँ \ (1; 2; ...; n \ दाएँ \) $ पर परिभाषित किया गया है और इस सेट को स्वयं पर ही मैप करता है। $ ((p) _ (1)) $, $ ((p) _ (2)) $ और $ ((p) _ (3)) $ के सिर्फ लिखित क्रमपरिवर्तन पर लौटने पर, हम काफी कानूनी रूप से लिख सकते हैं:

\ [((पी) _ (1)) \ बाएं (1 \ दाएं) = 1; ((पी) _ (2)) \ बाएं (3 \ दाएं) = 2; ((पी) _ (3)) \ बाएँ (2 \ दाएँ) = 4; \]

लंबाई $ n $ के विभिन्न क्रमपरिवर्तनों की संख्या हमेशा बंधी हुई होती है और $ n! $ के बराबर होती है - यह कॉम्बिनेटरिक्स से आसानी से सिद्ध होने वाला तथ्य है। उदाहरण के लिए, यदि हम लंबाई 5 के सभी क्रमपरिवर्तन लिखना चाहते हैं, तो हम बहुत हिचकिचाएंगे, क्योंकि ऐसे क्रमपरिवर्तन होंगे

किसी भी क्रमपरिवर्तन की प्रमुख विशेषताओं में से एक इसमें व्युत्क्रमों की संख्या है।

परिभाषा। क्रमचय में उलटा $ p = \ बाएँ (((a) _ (1)); ((a) _ (2)); ...; ((a) _ (n)) \ दाएँ) $ - कोई भी जोड़ा $ \ बाएँ (((a) _ (i)); ((a) _ (j)) \ दाएँ) $ ऐसा कि $ i \ lt j $, लेकिन $ ((a) _ (i)) \ gt ( ( ए) _ (जे)) $। सीधे शब्दों में कहें, एक उलटा तब होता है जब एक छोटी संख्या के बाईं ओर एक बड़ी संख्या होती है (जरूरी नहीं कि आसन्न एक)।

हम $ N \ बाएँ (p \ दाएँ) $ द्वारा क्रमचय $ p $ में व्युत्क्रमों की संख्या को निरूपित करेंगे, लेकिन विभिन्न पाठ्यपुस्तकों और विभिन्न लेखकों में अन्य पदनामों को पूरा करने के लिए तैयार रहें - यहाँ कोई समान मानक नहीं हैं। व्युत्क्रम का विषय बहुत व्यापक है, और इसके लिए एक अलग पाठ समर्पित किया जाएगा। अब हमारा काम केवल यह सीखना है कि उन्हें वास्तविक समस्याओं में कैसे गिनें।

उदाहरण के लिए, आइए क्रमचय $ p = \ बाएँ (1; 4; 5; 3; 2 \ दाएँ) $ में व्युत्क्रमों की संख्या गिनें:

\ [\ बाएँ (4; 3 \ दाएँ); \ बाएँ (4; 2 \ दाएँ); \ बाएँ (5; 3 \ दाएँ); \ बाएँ (5; 2 \ दाएँ); \ बाएँ (3; 2 \ दाएँ) ) \]

तो $ N \ बाएँ (p \ दाएँ) = 5 $। जैसा कि आप देख सकते हैं, इसमें कुछ भी गलत नहीं है। मैं आपको तुरंत बता दूं: आगे हमें $ N \ बाएँ (p \ दाएँ) $ की संख्या में उतनी दिलचस्पी नहीं होगी जितनी कि इसकी समता / विषमता में। और यहाँ हम आसानी से आज के पाठ के मुख्य शब्द की ओर बढ़ते हैं।

एक निर्धारक क्या है

मान लीजिए एक वर्ग आव्यूह $ A = \ बाएँ [n \ बार n \ दाएँ] $ दिया जाए। फिर:

परिभाषा। मैट्रिक्स का निर्धारक $ A = \ बाएँ [n \ बार n \ दाएँ] $ $ n! $ शर्तों का बीजगणितीय योग है, जिसकी रचना इस प्रकार है। प्रत्येक शब्द $ n $ मैट्रिक्स तत्वों का उत्पाद है, प्रत्येक पंक्ति और प्रत्येक कॉलम से एक लिया जाता है, जिसे (-1) से गुणा करके व्युत्क्रमों की संख्या की शक्ति से गुणा किया जाता है:

\ [\ बाएं | ए \ सही | = \ योग \ सीमाएं_ (एन{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}

सारणिक में प्रत्येक पद के लिए गुणनखंड चुनने का मूल बिंदु यह तथ्य है कि कोई भी दो गुणनखंड एक ही पंक्ति में या एक ही स्तंभ में नहीं होते हैं।

इसके कारण, हम सामान्यता के नुकसान के बिना मान सकते हैं कि सूचकांक $ i $ कारकों के $ ((a) _ (i; j)) $ "रन" मान 1, ..., $ n $ , और सूचकांक $ j $ पहले के कुछ क्रमपरिवर्तन हैं:

और जब कोई क्रमपरिवर्तन $ p $ होता है, तो हम आसानी से $ N \ बाएँ (p \ दाएँ) $ के व्युत्क्रम की गणना कर सकते हैं - और सारणिक का अगला पद तैयार है।

स्वाभाविक रूप से, कोई भी किसी भी अवधि में गुणकों की अदला-बदली करने से मना नहीं करता है (या उन सभी में एक ही बार में - ट्राइफल्स पर समय क्यों बर्बाद करें?), और फिर पहले सूचकांक भी कुछ क्रमपरिवर्तन का प्रतिनिधित्व करेंगे। लेकिन अंत में, कुछ भी नहीं बदलेगा: इंडेक्स $ i $ और $ j $ में व्युत्क्रमों की कुल संख्या ऐसी विकृतियों के तहत समानता को बरकरार रखती है, जो कि अच्छे पुराने नियम के अनुरूप है:

गुणनखंडों को पुनर्व्यवस्थित करने से संख्याओं का गुणनफल नहीं बदलता है।

बस इस नियम को मैट्रिक्स गुणन से न बांधें - संख्या गुणन के विपरीत, यह कम्यूटिव नहीं है। लेकिन मैं पीछे हटा। :)

मैट्रिक्स 2x2

वास्तव में, आप 1x1 मैट्रिक्स पर विचार कर सकते हैं - यह एक सेल होगा, और इसका निर्धारक, जैसा कि आप अनुमान लगा सकते हैं, इस सेल में लिखी संख्या के बराबर है। कुछ खास दिलचस्प नहीं।

तो आइए 2x2 वर्ग मैट्रिक्स पर विचार करें:

\ [\ बाएं [\ शुरू (मैट्रिक्स) ((ए) _ (11)) और ((ए) _ (12)) \\ ((ए) _ (21)) और ((ए) _ (22)) \\\ अंत (मैट्रिक्स) \ दाएं] \]

चूँकि इसमें रेखाओं की संख्या $ n = 2 $ है, सारणिक में $ n! = 2! = 1 \ cdot 2 = 2 $ पद होंगे। आइए उन्हें लिखते हैं:

\ [\ start (संरेखण) और ((\ बाएँ (-1 \ दाएँ)) ^ (N \ बाएँ (1; 2 \ दाएँ)) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((\ बाएँ (-1 \ दाएँ)) ^ (0)) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((a) _ (11)) ((ए) _ (22)); \\ और ((\ बाएँ (-1 \ दाएँ)) ^ (N \ बाएँ (2; 1 \ दाएँ))) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((\ बाएँ (-1 \ दाएँ)) ^ (1)) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((a) _ (12)) ( (ए) _ (21))। \\\ अंत (संरेखित करें) \]

जाहिर है, क्रमपरिवर्तन $ \ बाएँ (1; 2 \ दाएँ) $ में कोई व्युत्क्रम नहीं है, जिसमें दो तत्व होते हैं, इसलिए $ N \ बाएँ (1; 2 \ दाएँ) = 0 $। लेकिन क्रमपरिवर्तन में $ \ बाएँ (2; 1 \ दाएँ) $ एक उलटा है (वास्तव में, 2< 1), поэтому $N\left(2;1 \right)=1.$

कुल मिलाकर, 2x2 मैट्रिक्स के लिए सारणिक की गणना के लिए सार्वभौमिक सूत्र इस तरह दिखता है:

\ [\ बाएं | \ शुरू (मैट्रिक्स) ((ए) _ (11)) और ((ए) _ (12)) \\ ((ए) _ (21)) और ((ए) _ (22)) \\\ अंत ( मैट्रिक्स) \ सही | = ((ए) _ (11)) ((ए) _ (22)) - ((ए) _ (12)) ((ए) _ (21)) \]

ग्राफिक रूप से, इसे मुख्य विकर्ण पर तत्वों के उत्पाद के रूप में दर्शाया जा सकता है, एक तरफ तत्वों के उत्पाद को घटाकर:

आइए कुछ उदाहरण देखें:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 5 और 6 \\ 8 और 9 \\\ अंत (मैट्रिक्स) \ दाएँ |; \ क्वाड \ बाएँ | \ शुरू (मैट्रिक्स) 7 और 12 \\ 14 और 1 \\\ अंत (मैट्रिक्स) \ सही |। \]

समाधान। सब कुछ एक पंक्ति में गिना जाता है। पहला मैट्रिक्स:

और दूसरा वाला:

उत्तर: -3; −161.

हालाँकि, यह बहुत आसान था। आइए 3x3 मैट्रिक्स देखें - यह वहां पहले से ही दिलचस्प है।

3x3 मैट्रिक्स

अब एक 3x3 वर्ग मैट्रिक्स पर विचार करें:

\ [\ बाएं [\ शुरू (मैट्रिक्स) ((ए) _ (11)) और ((ए) _ (12)) और ((ए) _ (13)) \\ ((ए) _ (21)) और ((ए) _ (22)) और ((ए) _ (23)) \\ ((ए) _ (31)) और ((ए) _ (32)) और ((ए) _ (33) ) \\\ अंत (मैट्रिक्स) \ दाएं] \]

इसके निर्धारक की गणना करते समय, हमें $ 3! = 1 \ cdot 2 \ cdot 3 = 6 $ शब्द मिलते हैं - घबराहट के लिए बहुत अधिक नहीं, लेकिन कुछ नियमितताओं की तलाश शुरू करने के लिए पर्याप्त है। सबसे पहले, आइए तीन तत्वों के सभी क्रमपरिवर्तन लिखें और उनमें से प्रत्येक में व्युत्क्रम की गणना करें:

\ [\ शुरू (संरेखण) और ((पी) _ (1)) = \ बाएँ (1; 2; 3 \ दाएँ) \ दायाँ तीर N \ बाएँ (((p) _ (1)) \ दाएँ) = N \ बाएँ (1; 2; 3 \ दाएँ) = 0; \\ & ((p) _ (2)) = \ बाएँ (1; 3; 2 \ दाएँ) \ दाएँ तीर N \ बाएँ (((p) _ (2)) \ दाएँ) = N \ बाएँ (1; 3 ; 2 \ दाएं) = 1; \\ & ((p) _ (3)) = \ बाएँ (2; 1; 3 \ दाएँ) \ दाएँ तीर N \ बाएँ (((p) _ (3)) \ दाएँ) = N \ बाएँ (2; 1 ; 3 \ दाएं) = 1; \\ & ((p) _ (4)) = \ बाएँ (2; 3; 1 \ दाएँ) \ दाएँ तीर N \ बाएँ (((p) _ (4)) \ दाएँ) = N \ बाएँ (2; 3 ; 1 \ दाएं) = 2; \\ & ((p) _ (5)) = \ बाएँ (3; 1; 2 \ दाएँ) \ दाएँ तीर N \ बाएँ (((p) _ (5)) \ दाएँ) = N \ बाएँ (3; 1 ; २ \ दाएँ) = २; \\ & ((p) _ (6)) = \ बाएँ (3; 2; 1 \ दाएँ) \ दाएँ तीर N \ बाएँ (((p) _ (6)) \ दाएँ) = N \ बाएँ (3; 2 ; 1 \ दाएँ) = 3। \\\ अंत (संरेखित करें) \]

जैसा कि अपेक्षित था, कुल 6 क्रमपरिवर्तन $ ((p) _ (1)) $, ... $ ((p) _ (6)) $ लिखे गए थे, और उनमें व्युत्क्रमों की संख्या 0 से बदल जाती है। से 3.

सामान्य तौर पर, हमारे पास "प्लस" के साथ तीन शब्द होंगे (जहाँ $ N \ बाएँ (p \ दाएँ) $ सम है) और तीन और "माइनस" के साथ। सामान्य तौर पर, निर्धारक की गणना सूत्र के अनुसार की जाएगी:

\ [\ बाएं | \ शुरू (मैट्रिक्स) ((ए) _ (11)) और ((ए) _ (12)) और ((ए) _ (13)) \\ ((ए) _ (21)) और ((ए) _ (22)) और ((ए) _ (23)) \\ ((ए) _ (31)) और ((ए) _ (32)) और ((ए) _ (33)) \\\ अंत (मैट्रिक्स) \ सही | = \ शुरू (मैट्रिक्स) ((ए) _ (11)) ((ए) _ (22)) ((ए) _ (33)) + ((ए) _ (12)) ( (ए) _ (23)) ((ए) _ (31)) + ((ए) _ (13)) ((ए) _ (21)) ((ए) _ (32)) - \\ - ( (ए) _ (13)) ((ए) _ (22)) ((ए) _ (31)) - ((ए) _ (12)) ((ए) _ (21)) ((ए) _ (33)) - ((ए) _ (11)) ((ए) _ (23)) ((ए) _ (32)) \\\ अंत (मैट्रिक्स) \]

बस बैठो मत और इन सभी सूचकांकों को अब जमकर रौंदो! अतुलनीय संख्याओं के बजाय, निम्नलिखित स्मरणीय नियम को याद रखना बेहतर है:

त्रिभुज नियम। 3x3 मैट्रिक्स के निर्धारक को खोजने के लिए, आपको मुख्य विकर्ण पर तत्वों के तीन उत्पादों को जोड़ने की जरूरत है और इस विकर्ण के समानांतर एक समद्विबाहु त्रिभुज के कोने पर, और फिर समान तीन उत्पादों को घटाएं, लेकिन साइड विकर्ण पर। योजनाबद्ध रूप से, यह इस तरह दिखता है:

3x3 मैट्रिक्स निर्धारक: त्रिभुज नियम

यह ये त्रिकोण हैं (या पेंटाग्राम - जैसा आप चाहते हैं) वे बीजगणित पर सभी प्रकार की पाठ्यपुस्तकों और मैनुअल में आकर्षित करना पसंद करते हैं। हालांकि, आइए दुखद चीजों के बारे में बात न करें। आइए ऐसे एक निर्धारक की बेहतर गणना करें - असली टिन से पहले वार्म-अप के लिए। :)

कार्य। निर्धारक की गणना करें:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 1 और 2 और 3 \\ 4 और 5 और 6 \\ 7 और 8 और 1 \\\ अंत (मैट्रिक्स) \ दाएं | \]

समाधान। हम त्रिकोण के नियम के अनुसार काम करते हैं। सबसे पहले, हम तीन शब्दों की गणना करते हैं, जो मुख्य विकर्ण पर तत्वों से बने होते हैं और इसके समानांतर होते हैं:

\ [\ start (संरेखण) और 1 \ cdot 5 \ cdot 1 + 2 \ cdot 6 \ cdot 7 + 3 \ cdot 4 \ cdot 8 = \\ & = 5 + 84 + 96 = 185 \\\ अंत (संरेखित) \]

अब हम पक्ष विकर्ण से निपटते हैं:

\ [\ start (संरेखण) और 3 \ cdot 5 \ cdot 7 + 2 \ cdot 4 \ cdot 1 + 1 \ cdot 6 \ cdot 8 = \\ & = 105 + 8 + 48 = 161 \\\ अंत (संरेखित) \]

यह केवल पहली संख्या से दूसरे को घटाने के लिए बनी हुई है - और हमें उत्तर मिलेगा:

बस इतना ही!

हालांकि, 3x3 मैट्रिक्स निर्धारक अभी तक कौशल का शिखर नहीं हैं। सबसे दिलचस्प बात आगे हमारा इंतजार कर रही है। :)

निर्धारकों की गणना के लिए सामान्य योजना

जैसा कि हम जानते हैं, जैसे-जैसे मैट्रिक्स का आयाम $ n $ बढ़ता है, सारणिक में पदों की संख्या $ n! $ होती है और तेजी से बढ़ती है। आखिरकार, फैक्टोरियल आपके लिए कोई बहुत बुरी चीज नहीं है, बल्कि तेजी से बढ़ता हुआ कार्य है।

पहले से ही 4x4 मैट्रिक्स के लिए, निर्धारकों को सीधे आगे पढ़ना बहुत अच्छा नहीं हो जाता है (यानी क्रमपरिवर्तन के माध्यम से)। लगभग 5x5 और अधिक सामान्यतः चुप रहते हैं। इसलिए, निर्धारक के कुछ गुण मामले से जुड़े होते हैं, लेकिन उन्हें समझने के लिए थोड़ी सैद्धांतिक तैयारी की आवश्यकता होती है।

तैयार? जाना!

मैट्रिक्स माइनर क्या है

मान लीजिए कि एक मनमाना मैट्रिक्स $ A = \ बाएँ [m \ बार n \ दाएँ] $ दिया जाता है। नोट: जरूरी नहीं कि चौकोर हो। निर्धारकों के विपरीत, अवयस्क ऐसी चीजें हैं जो न केवल कठोर वर्ग मैट्रिक्स में मौजूद हैं। आइए हम इस मैट्रिक्स में $ 1 \ le k \ le m $ और $ 1 \ le k \ le n $ के साथ कई (उदाहरण के लिए, $ k $) पंक्तियों और स्तंभों को चुनें। फिर:

परिभाषा। ऑर्डर का माइनर $ k $ चयनित $ k $ कॉलम और पंक्तियों के चौराहे पर उत्पन्न होने वाले वर्ग मैट्रिक्स का निर्धारक है। हम इस नए मैट्रिक्स को माइनर भी कहेंगे।

ऐसे नाबालिग को $ ((M) _ (k)) $ के रूप में दर्शाया जाता है। स्वाभाविक रूप से, एक मैट्रिक्स में $ k $ के क्रम के नाबालिगों का एक पूरा समूह हो सकता है। यहाँ $ \ बाएँ [5 \ बार 6 \ दाएँ] $ मैट्रिक्स के लिए एक मामूली क्रम 2 का एक उदाहरण दिया गया है:

नाबालिग बनाने के लिए $ k = 2 $ कॉलम और पंक्तियों का चयन करना

यह आवश्यक नहीं है कि चयनित पंक्तियों और स्तंभों को एक साथ रखा जाए, जैसा कि ऊपर दिए गए उदाहरण में है। मुख्य बात यह है कि चयनित पंक्तियों और स्तंभों की संख्या समान है (यह संख्या $ k $ है)।

एक और परिभाषा भी है। शायद कोई इसे और पसंद करेगा:

परिभाषा। मान लीजिए एक आयताकार आव्यूह $ A = \ बाएँ [m \ बार n \ दाएँ] $ दिया जाए। यदि एक या कई कॉलम और उसमें एक या कई पंक्तियों को हटाने के बाद, आकार $ \ बाएँ [k \ बार k \ दाएँ] $ का एक वर्ग मैट्रिक्स बनता है, तो इसका निर्धारक मामूली $ ((M) _ (k) है ) $... हम कभी-कभी मैट्रिक्स को स्वयं नाबालिग भी कहेंगे - यह संदर्भ से स्पष्ट होगा।

जैसा कि मेरी बिल्ली कहा करती थी, कभी-कभी बालकनी पर बैठकर म्याऊ करने की तुलना में 11वीं मंजिल से उठकर एक बार खाना खा लेना बेहतर होता है।

उदाहरण। एक मैट्रिक्स दिया गया

पंक्ति 1 और कॉलम 2 को चुनना, हमें प्रथम-क्रम नाबालिग मिलता है:

\ [((एम) _ (1)) = \ बाएं | 7 \ दाएं | = 7 \]

पंक्तियों 2, 3 और कॉलम 3, 4 को चुनना, हमें दूसरे क्रम का एक नाबालिग मिलता है:

\ [((एम) _ (2)) = \ बाएं | \ शुरू (मैट्रिक्स) 5 और 3 \\ 6 और 1 \\\ अंत (मैट्रिक्स) \ दाएं | = 5-18 = -13 \]

और यदि आप सभी तीन पंक्तियों के साथ-साथ कॉलम 1, 2, 4 का चयन करते हैं, तो तीसरे क्रम का नाबालिग होगा:

\ [((एम) _ (3)) = \ बाएं | \ शुरू (मैट्रिक्स) 1 और 7 और 0 \\ 2 और 4 और 3 \\ 3 और 0 और 1 \\\ अंत (मैट्रिक्स) \ दाएं | \]

पाठक के लिए आदेश 1, 2, या 3 के अन्य नाबालिगों को ढूंढना मुश्किल नहीं होगा। इसलिए, चलिए आगे बढ़ते हैं।

बीजीय पूरक

"ठीक है, और ये मिनियन हमें क्या देते हैं?" - आप शायद पूछें। अपने आप से, कुछ भी नहीं। लेकिन वर्ग मैट्रिक्स में, प्रत्येक नाबालिग का एक "साथी" होता है - एक अतिरिक्त नाबालिग, साथ ही एक बीजीय पूरक। और साथ में, ये दो तरकीबें हमें नट्स जैसे क्वालिफायर पर क्लिक करने की अनुमति देंगी।

परिभाषा। मान लीजिए कि एक वर्ग मैट्रिक्स $ A = \ बाएँ [n \ बार n \ दाएँ] $ दिया जाता है, जिसमें मामूली $ ((M) _ (k)) $ चुना जाता है। फिर नाबालिग $ ((M) _ (k)) $ के लिए अतिरिक्त नाबालिग मूल मैट्रिक्स $ A $ का एक टुकड़ा है, जो नाबालिग $ ((M) _ ((M)) की रचना में शामिल सभी पंक्तियों और स्तंभों को हटाने के बाद रहता है। के)) $:

अतिरिक्त अवयस्क से अवयस्क $ ((M) _ (2)) $

आइए एक बिंदु को स्पष्ट करें: एक अतिरिक्त नाबालिग केवल "मैट्रिक्स का टुकड़ा" नहीं है, बल्कि इस टुकड़े का निर्धारक है।

अतिरिक्त नाबालिगों को तारांकन चिह्न से दर्शाया जाता है: $ M_ (k) ^ (*) $:

जहां ऑपरेशन $ A \ nabla ((M) _ (k)) $ का शाब्दिक अर्थ है "$ A $ से पंक्तियों और स्तंभों को $ ((M) _ (k)) $ में शामिल करें"। यह ऑपरेशन आम तौर पर गणित में स्वीकार नहीं किया जाता है - मैंने इसे कहानी की सुंदरता के लिए खुद ही आविष्कार किया है। :)

पूरक नाबालिगों का उपयोग शायद ही कभी अपने दम पर किया जाता है। वे एक अधिक जटिल निर्माण, बीजीय पूरक का हिस्सा हैं।

परिभाषा। मामूली पूरक $ ((M) _ (k)) $ अतिरिक्त नाबालिग $ M_ (k) ^ (*) $ को $ से गुणा किया जाता है ((\ बाएँ (-1 \ दाएँ)) ^ (S)) $ , जहाँ $ S $ मूल नाबालिग $ ((M) _ (k)) $ में शामिल सभी पंक्तियों और स्तंभों की संख्या का योग है।

एक नियम के रूप में, बीजीय लघु पूरक $ ((M) _ (k)) $ को $ ((A) _ (k)) $ द्वारा दर्शाया जाता है। इसीलिए:

\ [((ए) _ (के)) = ((\ बाएं (-1 \ दाएं)) ^ (एस)) \ cdot M_ (के) ^ (*) \]

मुश्किल? पहली नज़र में, हाँ। लेकिन यह ठीक नहीं है. क्योंकि वास्तव में सब कुछ आसान है। आइए एक उदाहरण पर विचार करें:

उदाहरण। एक 4x4 मैट्रिक्स दिया गया है:

आइए दूसरे क्रम के नाबालिग को चुनें

\ [((एम) _ (2)) = \ बाएं | \ शुरू (मैट्रिक्स) 3 और 4 \\ 15 और 16 \\\ अंत (मैट्रिक्स) \ दाएं | \]

कप्तान स्पष्ट हमें संकेत दे रहा है कि लाइन 1 और 4, साथ ही कॉलम 3 और 4, इस नाबालिग को संकलित करने में शामिल थे। उन्हें पार करें - हमें एक अतिरिक्त नाबालिग मिलता है:

यह संख्या $ S $ खोजने और बीजीय पूरक प्राप्त करने के लिए बनी हुई है। चूंकि हम शामिल पंक्तियों (1 और 4) और कॉलम (3 और 4) की संख्या जानते हैं, सब कुछ सरल है:

\ [\ शुरू (संरेखित करें) और एस = 1 + 4 + 3 + 4 = 12; \\ & ((ए) _ (2)) = ((\ बाएं (-1 \ दाएं)) ^ (एस)) \ cdot M_ (2) ^ (*) = ((\ बाएं (-1 \ दाएं) ) ^ (12)) \ cdot \ बाएँ (-4 \ दाएँ) = - 4 \ अंत (संरेखित) \]

उत्तर: $ ((ए) _ (2)) = - 4 $

बस इतना ही! वास्तव में, एक अतिरिक्त नाबालिग और एक बीजीय पूरक के बीच सभी अंतर केवल सामने के ऋण में हैं, और तब भी हमेशा नहीं।

लाप्लास की प्रमेय

और इसलिए हम इस बात पर पहुंचे कि वास्तव में, इन सभी नाबालिगों और बीजीय जोड़ की आवश्यकता क्यों थी।

सारणिक के विस्तार पर लाप्लास का प्रमेय। मान लें कि $ k $ पंक्तियों (स्तंभों) को आकार के मैट्रिक्स में $ \ बाएँ [n \ बार n \ दाएँ] $, $ 1 \ le k \ le n-1 $ के साथ चुना जाता है। फिर इस मैट्रिक्स का निर्धारक उनके बीजगणितीय पूरक द्वारा चयनित पंक्तियों (स्तंभों) में निहित $ k $ क्रम के नाबालिगों के सभी उत्पादों के योग के बराबर है:

\ [\ बाएं | ए \ सही | = \ योग (((एम) _ (के)) \ cdot ((ए) _ (के))) \]

इसके अलावा, बिल्कुल $ C_ (n) ^ (k) $ ऐसी शर्तें होंगी।

ठीक है, ठीक है: लगभग $ C_ (n) ^ (k) $ - मैं पहले से ही इसके बारे में बात कर रहा हूं, मूल लाप्लास के प्रमेय में ऐसा कुछ नहीं था। लेकिन किसी ने भी कॉम्बिनेटरिक्स को रद्द नहीं किया, और वस्तुतः इस स्थिति पर एक सरसरी निगाह आपको यह सुनिश्चित करने की अनुमति देगी कि वास्तव में बहुत सारी शर्तें होंगी। :)

हम इसे साबित नहीं करेंगे, हालांकि यह कोई विशेष कठिनाई पेश नहीं करता है - सभी गणनाओं को अच्छे पुराने क्रमपरिवर्तन और सम/विषम व्युत्क्रमों में घटा दिया जाता है। फिर भी, सबूत एक अलग पैराग्राफ में प्रस्तुत किया जाएगा, और आज हमारे पास एक विशुद्ध रूप से व्यावहारिक सबक है।

इसलिए, हम इस प्रमेय के एक विशेष मामले को पास करते हैं, जब नाबालिग मैट्रिक्स के अलग-अलग सेल होते हैं।

पंक्ति और स्तंभ द्वारा निर्धारक अपघटन

अब जिस पर चर्चा की जाएगी, वह निर्धारकों के साथ काम करने का मुख्य उपकरण है, जिसके लिए क्रमपरिवर्तन, नाबालिगों और बीजगणितीय परिवर्धन के साथ यह सारा खेल शुरू किया गया था।

पढ़ें और आनंद लें:

लाप्लास के प्रमेय से परिणाम (निर्धारक की पंक्ति/स्तंभ विस्तार)। एक पंक्ति को आकार के मैट्रिक्स में $ \ बाएँ [n \ बार n \ दाएँ] $ चुनने दें। इस लाइन में नाबालिग $ n $ व्यक्तिगत सेल होंगे:

\ [((एम) _ (1)) = ((ए) _ (आईजे)), \ क्वाड जे = 1, ..., एन \]

अतिरिक्त नाबालिगों की गणना करना भी आसान है: बस मूल मैट्रिक्स लें और $ ((a) _ (ij)) $ वाली पंक्ति और कॉलम को हटा दें। आइए ऐसे नाबालिगों को $ M_ (ij) ^ (*) $ कहते हैं।

बीजगणितीय पूरक के लिए, संख्या $ S $ की अभी भी आवश्यकता है, लेकिन क्रम 1 के नाबालिग के मामले में, यह सेल $ ((a) _ (ij)) $ के "निर्देशांक" का योग है:

और फिर मूल निर्धारक को लाप्लास के प्रमेय के अनुसार $ ((a) _ (ij)) $ और $ M_ (ij) ^ (*) $ के संदर्भ में लिखा जा सकता है:

\ [\ बाएं | ए \ दायां | = \ योग \ सीमाएं_ (जे = 1) ^ (एन) (((ए) _ (आईजे)) \ cdot ((\ बाएं (-1 \ दाएं)) ^ (i + j)) \ cdot ((एम) _ (आईजे))) \]

यह वही है स्ट्रिंग विस्तार सूत्र... लेकिन कॉलम के लिए भी यही सच है।

इस परिणाम से कई निष्कर्ष निकाले जा सकते हैं:

1. यह योजना पंक्तियों और स्तंभों दोनों के लिए समान रूप से अच्छी तरह से काम करती है। वास्तव में, अधिक बार नहीं, विस्तार पंक्ति-वार के बजाय स्तंभ-वार होगा।
2. विस्तार में पदों की संख्या हमेशा $ n $ होती है। यह $ C_ (n) ^ (k) $ से काफी कम है और इससे भी अधिक $ n! $।
3. एक निर्धारक $ \ बाएँ [n \ बार n \ दाएँ] $ के बजाय, आपको आकार के कई निर्धारकों को एक कम गिनना होगा: $ \ बाएँ [\ बाएँ (n-1 \ दाएँ) \ बार \ बाएँ (n-1) \ दाएँ) \ दाएँ] $।

बाद वाला तथ्य विशेष रूप से महत्वपूर्ण है। उदाहरण के लिए, क्रूर 4x4 निर्धारक के बजाय, अब यह कई 3x3 निर्धारकों को गिनने के लिए पर्याप्त होगा - हम किसी तरह उनका सामना करेंगे। :)

कार्य। निर्धारक खोजें:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 1 और 2 और 3 \\ 4 और 5 और 6 \\ 7 और 8 और 9 \\\ अंत (मैट्रिक्स) \ दाएं | \]

समाधान। आइए इस निर्धारक को पहली पंक्ति के साथ विस्तारित करें:

\ [\ प्रारंभ (संरेखित करें) \ बाएँ | ए \ दाएँ | = 1 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (1 + 1)) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 5 और 6 \\ 8 और 9 \\\ अंत (मैट्रिक्स) \ दाएँ | + और \\ 2 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (1 + 2)) \ cdot \ बाएँ | \ start (मैट्रिक्स) 4 और 6 \\ 7 और 9 \\\ अंत (मैट्रिक्स) \ दाएँ | + और \\ 3 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (1 + 3)) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 4 और 5 \\ 7 और 8 \\\ अंत (मैट्रिक्स) \ दाएं | = और \\\ अंत (संरेखित) \]

\ [\ start (संरेखण) और = 1 \ cdot \ बाएँ (45-48 \ दाएँ) -2 \ cdot \ बाएँ (36-42 \ दाएँ) +3 \ cdot \ बाएँ (32-35 \ दाएँ) = \\ & = 1 \ cdot \ बाएँ (-3 \ दाएँ) -2 \ cdot \ बाएँ (-6 \ दाएँ) +3 \ cdot \ बाएँ (-3 \ दाएँ) = 0। \\\ अंत (संरेखित करें) \]

कार्य। निर्धारक खोजें:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 0 और 1 और 1 और 0 \\ 1 और 0 और 1 और 1 \\ 1 और 1 और 0 और 1 \\ 1 और 1 और 1 और 0 \\\ अंत (मैट्रिक्स) \ सही | \ ]

समाधान। एक बदलाव के लिए, इस बार कॉलम के साथ काम करते हैं। उदाहरण के लिए, अंतिम कॉलम में एक साथ दो शून्य होते हैं - जाहिर है, इससे गणना में काफी कमी आएगी। अब आप देखेंगे क्यों।

इसलिए, हम चौथे कॉलम द्वारा सारणिक का विस्तार करते हैं:

\ [\ प्रारंभ (संरेखित करें) \ बाएँ | \ शुरू (मैट्रिक्स) 0 और 1 और 1 और 0 \\ 1 और 0 और 1 और 1 \\ 1 और 1 और 0 और 1 \\ 1 और 1 और 1 और 0 \\\ अंत (मैट्रिक्स) \ सही | = 0 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (1 + 4)) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 0 और 1 \\ 1 और 1 और 0 \\ 1 और 1 और 1 \\\ अंत (मैट्रिक्स) \ दाएँ | + और \\ +1 \ cdot ((\ बाएँ (-1 \) दाएँ)) ^ (2 + 4)) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 0 और 1 और 1 \\ 1 और 1 और 0 \\ 1 और 1 और 1 \\\ अंत (मैट्रिक्स) \ दाएँ | + और \\ +1 \ cdot ((\ बाएँ (-1 \) दाएँ)) ^ (3 + 4)) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 0 और 1 और 1 \\ 1 और 0 और 1 \\ 1 और 1 और 1 \\\ अंत (मैट्रिक्स) \ दाएँ | + और \\ +0 \ cdot ((\ बाएँ (-1 \) दाएँ)) ^ (4 + 4)) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 0 और 1 और 1 \\ 1 और 0 और 1 \\ 1 और 1 और 0 \\\ अंत (मैट्रिक्स) \ सही | & \\\ अंत (संरेखित करें) \]

और फिर - ओह, चमत्कार! - दो शब्द तुरंत नीचे चले जाते हैं, क्योंकि उनके पास गुणक "0" होता है। अभी भी दो 3x3 निर्धारक हैं जिनसे हम आसानी से निपट सकते हैं:

\ [\ प्रारंभ (संरेखित करें) और \ बाएँ | \ शुरू (मैट्रिक्स) 0 और 1 और 1 \\ 1 और 1 और 0 \\ 1 और 1 और 1 \\\ अंत (मैट्रिक्स) \ दाएं | = 0 + 0 + 1-1-1-0 = -1; \\ और \ बाएं | \ शुरू (मैट्रिक्स) 0 और 1 और 1 \\ 1 और 0 और 1 \\ 1 और 1 और 1 \\\ अंत (मैट्रिक्स) \ दाएं | = 0 + 1 + 1-0-0-1 = 1। \\\ अंत (संरेखित करें) \]

हम स्रोत पर लौटते हैं और उत्तर पाते हैं:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 0 और 1 और 1 और 0 \\ 1 और 0 और 1 और 1 \\ 1 और 1 और 0 और 1 \\ 1 और 1 और 1 और 0 \\\ अंत (मैट्रिक्स) \ सही | = 1 \ cdot \ बाएँ (-1 \ दाएँ) + \ बाएँ (-1 \ दाएँ) \ cdot 1 = -2 \]

तो बस इतना ही। और नहीं 4! = 24 पदों को गिनने की आवश्यकता नहीं थी। :)

उत्तर: -2

निर्धारक के मूल गुण

पिछली समस्या में, हमने देखा कि कैसे एक मैट्रिक्स की पंक्तियों (स्तंभों) में शून्य की उपस्थिति सारणिक के विस्तार को और सामान्य तौर पर, सभी गणनाओं को सरल बनाती है। एक स्वाभाविक प्रश्न उठता है: क्या इन शून्यों को उस मैट्रिक्स में भी प्रकट करना संभव है जहां वे मूल रूप से नहीं थे?

उत्तर असंदिग्ध है: कर सकते हैं... और यहाँ निर्धारक के गुण हमारी सहायता के लिए आते हैं:

1. यदि आप दो पंक्तियों (स्तंभों) को स्थानों में अदला-बदली करते हैं, तो सारणिक नहीं बदलेगा;
2. यदि एक पंक्ति (स्तंभ) को संख्या $ k $ से गुणा किया जाता है, तो पूरे निर्धारक को भी $ k $ से गुणा किया जाता है;
3. यदि आप एक पंक्ति लेते हैं और इसे दूसरी से जितनी बार चाहें जोड़ (घटाना) करते हैं, तो सारणिक नहीं बदलेगा;
4. यदि सारणिक की दो रेखाएँ समान हों, या तो समानुपाती हों, या उनमें से एक रेखा शून्य से भरी हो, तो संपूर्ण सारणिक शून्य होता है;
5. उपरोक्त सभी गुण कॉलम के लिए भी सही हैं।
6. जब एक मैट्रिक्स को स्थानांतरित किया जाता है, तो निर्धारक नहीं बदलता है;
7. मैट्रिक्स उत्पाद का निर्धारक निर्धारकों के उत्पाद के बराबर होता है।

तीसरी संपत्ति विशेष मूल्य की है: हम कर सकते हैं एक पंक्ति (स्तंभ) से दूसरी घटाएं जब तक कि शून्य सही स्थानों पर दिखाई न दें.

अक्सर, गणना एक तत्व को छोड़कर, हर जगह पूरे कॉलम को "शून्य" करने के लिए उबालती है, और फिर इस कॉलम के साथ निर्धारक का विस्तार करती है, 1 कम आकार का मैट्रिक्स प्राप्त करती है।

आइए देखें कि यह व्यवहार में कैसे काम करता है:

कार्य। निर्धारक खोजें:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 1 और 2 और 3 और 4 \\ 4 और 1 और 2 और 3 \\ 3 और 4 और 1 और 2 \\ 2 और 3 और 4 और 1 \\\ अंत (मैट्रिक्स) \ सही | \ ]

समाधान। यहां कोई शून्य नहीं है, इसलिए आप किसी भी पंक्ति या स्तंभ पर "हथौड़ा" लगा सकते हैं - गणना की मात्रा लगभग समान होगी। आइए ट्राइफल्स पर समय बर्बाद न करें और पहले कॉलम को "शून्य" करें: इसमें पहले से ही एक के साथ एक सेल है, इसलिए बस पहली पंक्ति लें और इसे दूसरे से 4 बार, तीसरे से 3 बार और आखिरी से 2 बार घटाएं।

नतीजतन, हमें एक नया मैट्रिक्स मिलेगा, लेकिन इसका निर्धारक समान होगा:

\ [\ प्रारंभ (मैट्रिक्स) \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 2 और 3 और 4 \\ 4 और 1 और 2 और 3 \\ 3 और 4 और 1 और 2 \\ 2 और 3 और 4 और 1 \\\ अंत (मैट्रिक्स) \ सही | \ स्टार्ट (मैट्रिक्स) \ डाउनएरो \\ -4 \\ -3 \\ -2 \\\ एंड (मैट्रिक्स) = \\ = \ लेफ्ट | \ start (मैट्रिक्स) 1 और 2 और 3 और 4 \\ 4-4 \ cdot 1 और 1-4 \ cdot 2 और 2-4 \ cdot 3 और 3-4 \ cdot 4 \\ 3-3 \ cdot 1 & 4-3 \ cdot 2 और 1-3 \ cdot 3 और 2-3 \ cdot 4 \\ 2-2 \ cdot 1 और 3-2 \ cdot 2 और 4-2 \ cdot 3 और 1-2 \ cdot 4 \ \\ अंत (मैट्रिक्स) \ दाएँ | = \\ = \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 2 और 3 और 4 \\ 0 और -7 और -10 और -13 \\ 0 और -2 और -8 और -10 \\ 0 और -1 और -2 और -7 \\ \ अंत (मैट्रिक्स) \ दाएं | \\\ अंत (मैट्रिक्स) \]

अब, पिगलेट की समता के साथ, हम पहले कॉलम के अनुसार इस निर्धारक का विस्तार करते हैं:

\ [\ start (मैट्रिक्स) 1 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (1 + 1)) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) -7 और -10 और -13 \\ -2 और -8 और -10 \\ -1 और -2 और -7 \\\ अंत (मैट्रिक्स) \ सही | +0 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (2 + 1)) \ cdot \ बाएँ | ... \ दाएँ | + \\ +0 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (3 + 1)) \ cdot \ बाएँ | ... \ दाएँ | +0 \ cdot ((\ बाएँ (-1 \ दाएँ)) ^ (4 + 1)) \ cdot \ बाएँ | ... \ सही | \\\ अंत (मैट्रिक्स) \]

यह स्पष्ट है कि केवल पहला शब्द "जीवित" रहेगा - बाकी में मैंने निर्धारकों को भी नहीं लिखा था, क्योंकि वे वैसे भी शून्य से गुणा किए जाते हैं। सारणिक से पहले गुणांक एक के बराबर है, अर्थात। आपको इसे लिखने की आवश्यकता नहीं है।

लेकिन आप निर्धारक की तीनों पंक्तियों से "माइनस" निकाल सकते हैं। वास्तव में, हमने गुणनखंड (−1) को तीन बार हटा दिया:

\ [\ बाएं | \ शुरू (मैट्रिक्स) -7 और -10 और -13 \\ -2 और -8 और -10 \\ -1 और -2 और -7 \\\ अंत (मैट्रिक्स) \ दाएँ | = \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 7 और 10 और 13 \\ 2 और 8 और 10 \\ 1 और 2 और 7 \\\ अंत (मैट्रिक्स) \ दाएं | \]

हमें एक छोटा सा सारणिक 3x3 प्राप्त हुआ है, जिसे पहले से ही त्रिभुजों के नियम का उपयोग करके परिकलित किया जा सकता है। लेकिन हम इसे पहले कॉलम के अनुसार विघटित करने का प्रयास करेंगे - सौभाग्य से, अंतिम पंक्ति में गर्व से एक है:

\ [\ प्रारंभ (संरेखित करें) और \ बाएँ (-1 \ दाएँ) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 7 और 10 और 13 \\ 2 और 8 और 10 \\ 1 और 2 और 7 \\\ अंत (मैट्रिक्स) \ दाएं | \ शुरू (मैट्रिक्स) -7 \\ -2 \\ \ ऊपर की ओर \ \\ अंत (मैट्रिक्स) = \ बाएँ (-1 \ दाएँ) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 0 और -4 और -36 \\ 0 और -4 और -4 \\ 1 और 2 और 7 \\\ अंत (मैट्रिक्स) \ दाएँ | = \\ और = \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) -4 और -36 \\ 4 और -4 \\\ अंत (मैट्रिक्स) \ दाएँ | = \ बाएँ (-1 \ दाएँ) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) -4 और -36 \\ 4 और -4 \\\ अंत (मैट्रिक्स) \ सही | \\\ अंत (संरेखित करें) \]

बेशक, आप कुछ और मज़ेदार खेल सकते हैं और एक पंक्ति (कॉलम) में 2x2 मैट्रिक्स का विस्तार कर सकते हैं, लेकिन हम पर्याप्त हैं, इसलिए हम केवल उत्तर की गणना करेंगे:

\ [\ बाएँ (-1 \ दाएँ) \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) -4 और -36 \\ 4 और -4 \\\ अंत (मैट्रिक्स) \ दाएँ | = \ बाएँ (-1 \ दाएँ) \ cdot \ बाएँ (16 + 144 \ दाएँ) = - 160 \ ]

ऐसे ही सपने टूटते हैं। उत्तर में केवल -160। :)

उत्तर:-160.

अंतिम कार्य पर जाने से पहले कुछ नोट्स:

1. मूल मैट्रिक्स पक्ष विकर्ण के बारे में सममित था। विस्तार में सभी अवयस्क भी समान भुजा के विकर्ण के सापेक्ष सममित होते हैं।
2. कड़ाई से बोलते हुए, हम कुछ भी विस्तार नहीं कर सके, लेकिन मुख्य विकर्ण के नीचे ठोस शून्य होने पर मैट्रिक्स को ऊपरी त्रिकोणीय रूप में लाएं। फिर (ज्यामितीय व्याख्या के अनुसार, वैसे) निर्धारक मुख्य विकर्ण पर $ ((a) _ (ii)) $ - संख्याओं के उत्पाद के बराबर है।

कार्य। निर्धारक खोजें:

\ [\ बाएं | \ शुरू (मैट्रिक्स) 1 और 1 और 1 और 1 \\ 2 और 4 और 8 और 16 \\ 3 और 9 और 27 और 81 \\ 5 और 25 और 125 और 625 \\\ अंत (मैट्रिक्स) \ सही | \ ]

समाधान। खैर, यहाँ पहली पंक्ति "शून्य" होने की भीख माँगती है। हम पहला कॉलम लेते हैं और अन्य सभी से ठीक एक बार घटाते हैं:

\ [\ प्रारंभ (संरेखित करें) और \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 1 और 1 और 1 \\ 2 और 4 और 8 और 16 \\ 3 और 9 और 27 और 81 \\ 5 और 25 और 125 और 625 \\\ अंत (मैट्रिक्स) \ सही | = \\ और = \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 1-1 और 1-1 और 1-1 \\ 2 और 4-2 और 8-2 और 16-2 \\ 3 और 9-3 और 27-3 और 81-3 \\ 5 और 25-5 और 125-5 और 625-5 \\\ अंत (मैट्रिक्स) \ दाएँ | = \\ और = \ बाएँ | \ start (मैट्रिक्स) 1 और 0 और 0 और 0 \\ 2 और 2 और 6 और 14 \\ 3 और 6 और 24 और 78 \\ 5 और 20 और 120 और 620 \\\ अंत (मैट्रिक्स) \ सही | \\\ अंत (संरेखित करें) \]

हम पहली पंक्ति पर विस्तार करते हैं, और फिर हम शेष रेखाओं से सामान्य गुणनखंड निकालते हैं:

\ [\ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 2 और 6 और 14 \\ 6 और 24 और 78 \\ 20 और 120 और 620 \\\ अंत (मैट्रिक्स) \ दाएँ | = \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 3 और 7 \\ 1 और 4 और 13 \\ 1 और 6 और 31 \\\ अंत (मैट्रिक्स) \ दाएं | \]

फिर से हम "सुंदर" संख्याओं का निरीक्षण करते हैं, लेकिन पहले कॉलम में - हम इसके अनुसार निर्धारक का विस्तार करते हैं:

\ [\ start (संरेखित करें) और 240 \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 3 और 7 \\ 1 और 4 और 13 \\ 1 और 6 और 31 \\\ अंत (मैट्रिक्स) \ दाएं | \ शुरू (मैट्रिक्स) \ डाउनएरो \\ -1 \\ -1 \ \\ अंत (मैट्रिक्स) = 240 \ cdot \ बाएँ | \ शुरू (मैट्रिक्स) 1 और 3 और 7 \\ 0 और 1 और 6 \\ 0 और 3 और 24 \\\ अंत (मैट्रिक्स) \ दाएँ | = \\ और = 240 \ cdot ((\ बाएँ (-1 \) दाएँ)) ^ (1 + 1)) \ cdot \ बाएँ | \ start (मैट्रिक्स) 1 और 6 \\ 3 और 24 \\\ अंत (मैट्रिक्स) \ दाएँ | = \\ & = 240 \ cdot 1 \ cdot \ बाएँ (24-18 \ दाएँ) = 1440 \\\ अंत ( संरेखित करें) \]

आदेश। समस्या सुलझा ली गई है।

उत्तर: 1440

1. संकेतों का सामान्य नियम। निम्नलिखित के लिए, यह पता लगाना उपयोगी होगा कि सारणिक में शब्द किस चिन्ह से शामिल है, संख्याओं के दो क्रमपरिवर्तन कहाँ हैं।

यह पता लगाने के लिए, आपको कारकों को रेखाओं के क्रम में व्यवस्थित करना चाहिए। ध्यान दें कि यदि हम दो कारकों की अदला-बदली करते हैं, तो पहले और दूसरे दोनों सूचकांकों में एक स्थानान्तरण होता है, जिससे पहले सूचकांक में व्युत्क्रमों की संख्या और दूसरे सूचकांक में व्युत्क्रमों की संख्या विषम संख्याओं में बदल जाती है, और इसलिए उनका योग बदल जाता है। एक सम संख्या तक। इसलिए, यह दो कारकों के स्थानों में परिवर्तन के साथ नहीं बदलता है, और, परिणामस्वरूप, कारकों के क्रम में किसी भी परिवर्तन के साथ, क्योंकि क्रम में कोई भी परिवर्तन स्थानों के कई जोड़ीदार परिवर्तनों के बराबर है। इसलिए यह इस प्रकार है कि वह चिन्ह जिसके साथ पद सारणिक में प्रवेश करता है। दरअसल, गुणनखंडों को पंक्तियों के क्रम में लाने के बाद स्तंभ संख्याओं का क्रम होना चाहिए, ताकि तब

और यह कारक ± 1 है, जिसके साथ हमारे लिए ब्याज की अवधि निर्धारक में शामिल है।

2. स्थानांतरित मैट्रिक्स का निर्धारक मूल के बराबर है। दूसरे शब्दों में, मैट्रिक्स स्थानांतरित होने पर निर्धारक नहीं बदलता है।

दरअसल, मूल मैट्रिक्स के प्रत्येक पंक्ति से एक और प्रत्येक कॉलम से तत्वों के उत्पादों को लेना ट्रांसपोज़्ड मैट्रिक्स के संबंध में ऐसा करने जैसा ही है। इसके अलावा, मूल के लिए लाइन नंबर ट्रांसपोज़्ड के लिए कॉलम नंबर हैं, और मूल के लिए कॉलम नंबर ट्रांसपोज़्ड की लाइन नंबर हैं। इसलिए, प्रत्येक पद मूल मैट्रिक्स के निर्धारक में शामिल है और निर्धारक को एक ही कारक के साथ स्थानांतरित किया गया है

सेट किए गए दो गुण इंगित करते हैं कि क्वालीफायर में, पंक्तियाँ और स्तंभ पूरी तरह से समान हैं। इसलिए, पंक्तियों के लिए निर्धारित सभी और गुण कॉलम के लिए सही रहते हैं।

अगले दो गुणों का अर्थ है सारणिक की किसी भी रेखा के तत्वों के संबंध में रैखिकता।

3. यदि किसी रेखा के तत्वों को दो पदों के योग के रूप में प्रस्तुत किया जाता है, तो सारणिक दो सारणिकों के योग के बराबर होता है, जिनमें से पहली में चिह्नित रेखा के तत्व पहले जोड़ के बराबर होते हैं, दूसरे में - दूसरे को।

यदि हम मौखिक सूत्रीकरण से सूत्र की ओर बढ़ते हैं तो यह गुण अधिक पारदर्शी हो जाता है:

सबूत।

यह स्पष्ट है कि पहला योग बराबर है और दूसरा है

सिद्ध संपत्ति स्वाभाविक रूप से उस मामले में सामान्यीकृत होती है जब एक पंक्ति के तत्वों को कई शब्दों के योग के रूप में दर्शाया जाता है।

4. यदि सारणिक की किसी पंक्ति के सभी तत्वों का एक उभयनिष्ठ गुणनखंड हो, तो सारणिक के चिह्न से इस उभयनिष्ठ गुणनखंड को निकाला जा सकता है।

सचमुच,

5. दो समान तारों वाला सारणिक शून्य होता है।

6. यदि मैट्रिक्स में दो पंक्तियों की अदला-बदली की जाती है, तो इसका सारणिक संकेत को विपरीत में बदल देगा।

ये दो गुण निकट से संबंधित हैं और निर्धारकों के सिद्धांत में विशेष रूप से महत्वपूर्ण भूमिका निभाते हैं।

आइए पहले 5वीं संपत्ति को साबित करें, फिर 6 को।

मान लीजिए कि एक सारणिक दो समान तारों के साथ दिया गया है:

हम योग को विषम और सम क्रमपरिवर्तन के अनुरूप दो भागों में विभाजित करते हैं:

याद रखें कि सभी विषम क्रमपरिवर्तन प्राप्त होते हैं यदि सभी क्रमपरिवर्तनों में एक ही स्थानान्तरण किया जाता है। इसलिए,

परंतु । इसलिए, पहले योग में प्रत्येक पद के लिए, दूसरे में एक समान पद है, इसलिए यह साबित करने के लिए आवश्यक था।

आइए अब हम संपत्ति के प्रमाण की ओर मुड़ें, और आइए हम केवल I और II द्वारा अनुमत तारों को निरूपित करें। हमें निर्धारकों की तुलना करने की आवश्यकता है

इस प्रयोजन के लिए, एक सहायक निर्धारक पर विचार करें, जो शून्य के बराबर प्राथमिकता है:

हमने संपत्ति 3 का दो बार उपयोग किया।

पहली और चौथी शर्तें शून्य के बराबर हैं। नतीजतन, दूसरे और तीसरे का योग आवश्यक के रूप में शून्य के बराबर है।

गुण 5 और 6 को सिद्ध करने के एक अन्य तरीके पर विचार करें। आइए छठे से शुरू करें। रहने दो

दूसरे सारणिक से कोई भी पद लीजिए, जो उसकी पंक्तियों के क्रम में लिखा गया है:

यह एक गुणक के साथ शामिल है। लेकिन, इसलिए यह गुणक के साथ A में प्रवेश करता है। यह स्पष्ट है कि A से प्रत्येक पद विपरीत चिह्न के साथ A में प्रवेश करता है, अर्थात।

अब, गुण 5 को सिद्ध करने के लिए, दो समान तारों वाले एक सारणिक पर विचार करें और इन तारों को उलट दें। एक ओर, यह एक ही समय में संकेत बदलेगा, लेकिन साथ ही यह नहीं बदलेगा। अत, ।

हालाँकि, यह तर्क केवल तभी लागू होता है जब रिंग में 2 से विभाजन संभव हो, इसलिए यह निम्नानुसार है

अवशेष मॉड्यूल 2 के क्षेत्र में, हम ऐसा निष्कर्ष नहीं निकाल सके। यह पहले की तुलना में दूसरे प्रमाण में थोड़ी सी खामी है।

7. दो समानुपाती पंक्तियों वाला सारणिक शून्य होता है।

वास्तव में, यदि गुण 4 के अनुसार, हम सारणिक के चिह्न से परे आनुपातिकता गुणांक लेते हैं, तो समान रेखाओं वाला सारणिक रहता है, जो शून्य के बराबर होता है।

8. यदि आप किसी अन्य रेखा के समानुपाती संख्याओं को उसकी किसी रेखा में जोड़ते हैं तो सारणिक नहीं बदलता है।

सचमुच,

संपत्ति 8 विशेष रूप से महत्वपूर्ण है क्योंकि यह निर्धारकों की गणना के लिए एक कुंजी प्रदान करती है।

आइए एक छोटा सा उदाहरण देखें।

इसे सारणिक की गणना करने की आवश्यकता होने दें

दूसरी पंक्ति में पहली पंक्ति को -1 से गुणा करें, फिर पहले वाले को -1 से गुणा करके तीसरे में जोड़ें, और फिर पहले वाले को -1 से गुणा करके चौथे में जोड़ें। हमें एक समान सारणिक मिलता है

अब चौथी पंक्ति में तीसरी को -1 से गुणा करें, और चौथी पंक्ति में दूसरी को -1 से गुणा करें।

हमें एक समान सारणिक मिलता है

अब यह पता चला है कि निर्धारक के 24 पदों में से केवल एक गैर-शून्य है:। क्रमचय (1, 3, 2, 4) विषम है, इसलिए सारणिक -16 है।