एक जटिल चर z का एक रैखिक कार्य उस रूप का एक कार्य है जहाँ a और 6 को जटिल संख्याएँ दी जाती हैं, और a 0। स्वतंत्र चर z के सभी मानों के लिए एक रैखिक फ़ंक्शन परिभाषित किया गया है, यह एकल-मूल्यवान है और , चूँकि व्युत्क्रम फलन भी एकल-मान है, यह संपूर्ण समतल z में एकसमान है। एक रैखिक कार्य पूरे जटिल विमान में विश्लेषणात्मक होता है, और इसलिए इसका व्युत्पन्न पूरे विमान में इसके द्वारा किए गए मानचित्रण के अनुरूप होता है। एक रैखिक-आंशिक फ़ंक्शन फॉर्म का एक फ़ंक्शन है - दी गई जटिल संख्याएं, और एक रैखिक-आंशिक फ़ंक्शन को z = -| को छोड़कर स्वतंत्र चर zy के सभी मानों के लिए परिभाषित किया गया है, यह एकल-मूल्यवान है और, उलटा होने के बाद से फ़ंक्शन एक जटिल चर के प्राथमिक कार्य भिन्नात्मक-तर्कसंगत फ़ंक्शन पावर फ़ंक्शन एक्सपोनेंशियल फ़ंक्शन लॉगरिदमिक फ़ंक्शन त्रिकोणमितीय और हाइपरबॉलिक फ़ंक्शन एकल-मान हैं, पूरे जटिल विमान में असमान हैं, बिंदु को छोड़कर z = - इस क्षेत्र में, फ़ंक्शन (3) है विश्लेषणात्मक और इसके व्युत्पन्न, इसलिए, इसके द्वारा किया गया मानचित्रण अनुरूप है। आइए हम फ़ंक्शन (3) को बिंदु z = - \, सेटिंग t) = oo पर विस्तारित करें, और बिंदु को z(oo) = के साथ पत्राचार में अनंत w = oo पर रखें, फिर रैखिक-भिन्नात्मक फ़ंक्शन असमान होगा विस्तारित जटिल विमान z में। उदाहरण 1. एक रैखिक-भिन्नात्मक फलन पर विचार करें, समानता से यह निम्नानुसार है कि सम्मिश्र संख्याओं r और u के मापांक संबंध से संबंधित हैं और ये संख्याएँ स्वयं बिंदु O से निकलने वाली किरणों पर स्थित हैं और वास्तविक अक्ष के बारे में सममित हैं। विशेष रूप से, इकाई वृत्त के बिंदु |z| = 1 इकाई वृत्त N = 1 के बिंदुओं पर जाएं। इस मामले में, संयुग्म संख्या को सम्मिश्र संख्या (चित्र 11) को सौंपा गया है। यह भी ध्यान दें कि फलन r0 = -g अनंत r - oo से शून्य r0 - 0. 2.2 पर बिंदु को मैप करता है। पावर फ़ंक्शन एक पावर फ़ंक्शन जहां n एक प्राकृतिक संख्या है, पूरे जटिल विमान में विश्लेषणात्मक है; > 1 के लिए इसका अवकलज = nzn~] z = 0 को छोड़कर सभी बिंदुओं पर शून्येतर है। w और z को सूत्र (4) में घातांकीय रूप में लिखने पर, हम प्राप्त करते हैं कि सूत्र (5) से यह देखा जा सकता है कि सम्मिश्र संख्याएँ Z\ तथा z2 इस प्रकार कि जहाँ k एक पूर्णांक है, एक बिंदु w पर जाएँ। इसलिए, n > 1 मानचित्रण (4) के लिए z- तल पर एकसमान नहीं है। एक डोमेन का सबसे सरल उदाहरण जिसमें मैपिंग ri = zn असमान है, वह क्षेत्र है जहां कोई वास्तविक संख्या है। क्षेत्र (7) में, मानचित्रण (4) अनुरूप है। - बहु-मूल्यवान है, क्योंकि प्रत्येक सम्मिश्र संख्या z \u003d r1v 0 के लिए, आप n भिन्न सम्मिश्र संख्याएँ निर्दिष्ट कर सकते हैं, जैसे कि उनकी nth डिग्री z के बराबर है: ध्यान दें कि एक जटिल चर z की डिग्री n का बहुपद एक है फलन जहाँ सम्मिश्र संख्याएँ दी गई हैं, और ao 0. किसी भी डिग्री का बहुपद पूरे जटिल तल पर एक विश्लेषणात्मक कार्य है। 2.3. भिन्न-परिमेय फलन भिन्न-परिमेय फलन उस रूप का फलन है जहां) एक सम्मिश्र चर z के बहुपद हैं। एक भिन्नात्मक परिमेय फलन पूरे तल में विश्लेषणात्मक होता है, उन बिंदुओं को छोड़कर जहां हर Q(z) गायब हो जाता है। उदाहरण 3. ज़ुकोवस्की फ़ंक्शन पूरे विमान z में विश्लेषणात्मक है, बिंदु z = 0 को छोड़कर। आइए हम जटिल विमान के क्षेत्र की स्थितियों का पता लगाएं, जिसके तहत इस क्षेत्र में माना जाने वाला ज़ुकोवस्की फ़ंक्शन असमान होगा। एम अंक Z) और zj को फ़ंक्शन (8) द्वारा एक बिंदु पर स्थानांतरित करने दें। फिर, के लिए, हम इसे प्राप्त करते हैं इसलिए, ज़ुकोवस्की फ़ंक्शन की एकरूपता के लिए, यह आवश्यक और पर्याप्त है कि शर्त संतुष्ट हो। एक डोमेन का एक उदाहरण जो एकरूपता की स्थिति को संतुष्ट करता है (9) सर्कल का बाहरी हिस्सा है |z| > 1. चूंकि ज़ुकोवस्की फ़ंक्शन के व्युत्पन्न एक जटिल चर के प्राथमिक कार्य भिन्नात्मक-तर्कसंगत कार्य पावर फ़ंक्शन एक्सपोनेंशियल फ़ंक्शन लॉगरिदमिक फ़ंक्शन त्रिकोणमितीय और हाइपरबॉलिक फ़ंक्शन बिंदुओं को छोड़कर हर जगह गैर-शून्य हैं, तो इस फ़ंक्शन द्वारा किए गए क्षेत्र का मानचित्रण होगा अनुरूप (चित्र। 13)। ध्यान दें कि यूनिट डिस्क का इंटीरियर |I भी ज़ुकोवस्की फ़ंक्शन की एकरूपता का डोमेन है। चावल। 13 2.4. घातांकीय फलन हम किसी भी सम्मिश्र संख्या z = x + y के लिए घातांक फलन ez को निम्नानुसार परिभाषित करते हैं: x = 0 के लिए हमें यूलर सूत्र प्राप्त होता है: आइए हम घातांक फलन के मुख्य गुणों का वर्णन करें: 1. वास्तविक z के लिए, यह परिभाषा सामान्य के साथ मेल खाता है। इसे सूत्र (10) में y = 0 सेट करके सीधे सत्यापित किया जा सकता है। 2. फ़ंक्शन ez पूरे जटिल विमान पर विश्लेषणात्मक है, और इसके लिए सामान्य भेदभाव सूत्र संरक्षित है। 3. अतिरिक्त प्रमेय फ़ंक्शन ez के लिए संरक्षित है . मान लीजिए 4. फलन ez आवर्त है जिसमें काल्पनिक मुख्य आवर्त 2xi है। वास्तव में, किसी भी पूर्णांक k के लिए दूसरी ओर, यदि तब परिभाषा (10) से यह इस प्रकार है कि वह कहाँ से उसका अनुसरण करता है, या जहाँ n एक पूर्णांक है। पट्टी में संबंध (12) से संबंधित बिंदुओं की एक भी जोड़ी नहीं होती है, इसलिए यह अध्ययन से पता चलता है कि मानचित्रण w = e" पट्टी में असमान है (चित्र 14)। चूंकि यह एक व्युत्पन्न है, यह मानचित्रण है अनुरूप। टिप्पणी niv। फ़ंक्शन आरजी किसी भी पट्टी में असमान है 2.5 लॉगरिदमिक फ़ंक्शन जहां दिए गए समीकरण से, अज्ञात, हम प्राप्त करते हैं इसलिए, फ़ंक्शन के विपरीत फ़ंक्शन को किसी के लिए परिभाषित किया जाता है और सूत्र द्वारा दर्शाया जाता है जहां यह बहु- मान फ़ंक्शन को लॉगरिदमिक कहा जाता है और इसे निम्नानुसार दर्शाया जाता है, फिर Ln z के लिए सूत्र 2 प्राप्त होता है। 6. त्रिकोणमितीय और अतिपरवलयिक फलन वास्तविक y के लिए यूलर के सूत्र (11) से हम प्राप्त करते हैं। हम निम्नलिखित सूत्रों का उपयोग करके किसी भी सम्मिश्र संख्या z के लिए त्रिकोणमितीय फलन sin z और cos z परिभाषित करते हैं: एक जटिल तर्क के साइन और कोसाइन में दिलचस्प गुण होते हैं . आइए मुख्य सूची दें। फ़ंक्शन sinz और cos z: 1) वास्तविक z -x के लिए सामान्य ज्या और कोज्या के साथ मेल खाता है; 2) पूरे जटिल तल पर विश्लेषणात्मक हैं; 3) सामान्य विभेदन सूत्रों का पालन करें: 4) 2n की अवधि के साथ आवधिक हैं; 5) sin z - विषम फलन, a cos z - सम; 6) सामान्य त्रिकोणमितीय संबंध संरक्षित हैं। सभी सूचीबद्ध गुण सूत्र (15) से आसानी से प्राप्त हो जाते हैं। जटिल डोमेन में फ़ंक्शन tgz और ctgz को सूत्रों द्वारा परिभाषित किया जाता है, और हाइपरबोलिक फ़ंक्शन को सूत्रों द्वारा परिभाषित किया जाता है "हाइपरबोलिक फ़ंक्शन त्रिकोणमितीय कार्यों से निकटता से संबंधित हैं। यह संबंध निम्नलिखित समानता द्वारा व्यक्त किया गया है: एक जटिल तर्क के साइन और कोसाइन है एक अन्य महत्वपूर्ण गुण: जटिल तल पर | \ मनमाने ढंग से बड़े सकारात्मक गुण 6 और सूत्रों (18) का उपयोग करके, हम प्राप्त करते हैं कि एक जटिल चर के प्राथमिक कार्य भिन्नात्मक-तर्कसंगत कार्य पावर फ़ंक्शन एक्सपोनेंशियल फ़ंक्शन लॉगरिदमिक फ़ंक्शन त्रिकोणमितीय और हाइपरबॉलिक फ़ंक्शन जहां से मान लें कि हमारे पास है उदाहरण 4. यह जांचना आसान है कि -4 ,

एक जटिल चर के कार्य।
एक जटिल चर के कार्यों का अंतर।

यह लेख पाठों की एक श्रृंखला खोलता है जिसमें मैं एक जटिल चर के कार्यों के सिद्धांत से संबंधित विशिष्ट समस्याओं पर विचार करूंगा। उदाहरणों में सफलतापूर्वक महारत हासिल करने के लिए, आपको सम्मिश्र संख्याओं का बुनियादी ज्ञान होना चाहिए। सामग्री को समेकित और दोहराने के लिए, पृष्ठ पर जाने के लिए पर्याप्त है। खोजने के लिए आपको कौशल की भी आवश्यकता होगी दूसरा क्रम आंशिक व्युत्पन्न. यहाँ वे हैं, ये आंशिक व्युत्पन्न ... अब भी मैं थोड़ा आश्चर्यचकित था कि वे कितनी बार होते हैं ...

जिस विषय का हम विश्लेषण करना शुरू कर रहे हैं वह विशेष रूप से कठिन नहीं है, और एक जटिल चर के कार्यों में, सिद्धांत रूप में, सब कुछ स्पष्ट और सुलभ है। मुख्य बात मूल नियम का पालन करना है, जो मेरे द्वारा अनुभवजन्य रूप से प्राप्त किया गया है। पढ़ते रहिये!

एक जटिल चर के एक समारोह की अवधारणा

सबसे पहले, आइए एक चर के स्कूल फ़ंक्शन के बारे में अपने ज्ञान को ताज़ा करें:

एक चर का कार्यएक नियम है जिसके अनुसार स्वतंत्र चर का प्रत्येक मान (परिभाषा के क्षेत्र से) फ़ंक्शन के एक और केवल एक मान से मेल खाता है। स्वाभाविक रूप से, "x" और "y" वास्तविक संख्याएँ हैं।

जटिल मामले में, कार्यात्मक निर्भरता इसी तरह दी गई है:

एक जटिल चर का एकल-मूल्यवान कार्यनियम है कि हर कोई व्यापकस्वतंत्र चर का मान (डोमेन से) एक और केवल एक से मेल खाता है व्यापकसमारोह मूल्य। सिद्धांत रूप में, बहु-मूल्यवान और कुछ अन्य प्रकार के कार्यों पर भी विचार किया जाता है, लेकिन सादगी के लिए, मैं एक परिभाषा पर ध्यान केंद्रित करूंगा।

एक जटिल चर का कार्य क्या है?

मुख्य अंतर यह है कि संख्याएं जटिल हैं। मैं विडंबना नहीं कर रहा हूँ। इस तरह के सवालों से वे अक्सर स्तब्ध रह जाते हैं, लेख के अंत में मैं एक अच्छी कहानी बताऊंगा। सबक पर डमी के लिए जटिल संख्याहमने रूप में एक सम्मिश्र संख्या पर विचार किया। अब से "Z" अक्षर बन गया है चर, तो हम इसे इस प्रकार निरूपित करेंगे: , जबकि "x" और "y" अलग-अलग ले सकते हैं वैधमूल्य। मोटे तौर पर, एक जटिल चर का कार्य चर पर निर्भर करता है और जो "सामान्य" मान लेते हैं। निम्नलिखित बिंदु तार्किक रूप से इस तथ्य का अनुसरण करता है:

एक जटिल चर के कार्य को इस प्रकार लिखा जा सकता है:
, जहां और दो के दो कार्य हैं वैधचर।

समारोह कहा जाता है असली हिस्साकार्य।
समारोह कहा जाता है काल्पनिक हिस्साकार्य।

अर्थात्, एक सम्मिश्र चर का फलन दो वास्तविक फलनों और पर निर्भर करता है। अंत में सब कुछ स्पष्ट करने के लिए, आइए व्यावहारिक उदाहरण देखें:

उदाहरण 1

समाधान:स्वतंत्र चर "z", जैसा कि आपको याद है, इस प्रकार लिखा जाता है:

(1) मूल कार्य में प्रतिस्थापित।

(2) पहले पद के लिए, घटा हुआ गुणन सूत्र का उपयोग किया गया था। अवधि में, कोष्ठक खोले गए थे।

(3) ध्यान से चुकता करना, यह न भूलें

(4) शर्तों की पुनर्व्यवस्था: पहले शब्दों को फिर से लिखें , जिसमें कोई काल्पनिक इकाई नहीं है(पहला समूह), फिर पद, जहाँ (दूसरा समूह) है। यह ध्यान दिया जाना चाहिए कि शर्तों को फेरबदल करना आवश्यक नहीं है, और इस चरण को छोड़ दिया जा सकता है (वास्तव में, इसे मौखिक रूप से निष्पादित करके)।

(5) दूसरे समूह को कोष्ठक से निकाल दिया जाता है।

नतीजतन, हमारे कार्य को फॉर्म में दर्शाया गया है

उत्तर:
समारोह का असली हिस्सा है।
समारोह का काल्पनिक हिस्सा है।

ये कार्य क्या हैं? दो चर के सबसे सामान्य कार्य, जिनमें से कोई भी ऐसा लोकप्रिय पा सकता है आंशिक अवकलज. दया के बिना - हम पाएंगे। लेकिन थोड़ी देर बाद।

संक्षेप में, हल की गई समस्या का एल्गोरिथ्म निम्नानुसार लिखा जा सकता है: हम मूल कार्य में स्थानापन्न करते हैं, सरलीकरण करते हैं और सभी शब्दों को दो समूहों में विभाजित करते हैं - एक काल्पनिक इकाई (वास्तविक भाग) के बिना और एक काल्पनिक इकाई (काल्पनिक भाग) के साथ।

उदाहरण 2

किसी फलन का वास्तविक और काल्पनिक भाग ज्ञात कीजिए

यह स्वयं का उदाहरण है। इससे पहले कि आप अपने आप को जटिल विमान पर नग्न चेकर्स के साथ युद्ध में फेंक दें, मैं आपको इस विषय पर सबसे महत्वपूर्ण सलाह देता हूं:

ध्यान रहे!बेशक, आपको हर जगह सावधान रहने की जरूरत है, लेकिन जटिल संख्या में आपको पहले से कहीं ज्यादा सावधान रहना चाहिए! याद रखें कि, कोष्ठकों को सावधानीपूर्वक विस्तृत करें, कुछ भी न खोएं। मेरे प्रेक्षणों के अनुसार, सबसे सामान्य गलती चिन्ह का खो जाना है। जल्दी मत करो!

पाठ के अंत में पूर्ण समाधान और उत्तर।

अब घन। संक्षिप्त गुणन सूत्र का उपयोग करके, हम प्राप्त करते हैं:
.

अभ्यास में उपयोग करने के लिए सूत्र बहुत सुविधाजनक हैं, क्योंकि वे समाधान प्रक्रिया को बहुत तेज करते हैं।

एक जटिल चर के कार्यों का अंतर।

मेरे पास दो खबरें हैं: अच्छी और बुरी। मैं एक अच्छे से शुरू करूंगा। एक जटिल चर के एक समारोह के लिए, भेदभाव के नियम और प्राथमिक कार्यों के डेरिवेटिव की तालिका मान्य है। इस प्रकार, अवकलज को ठीक उसी तरह लिया जाता है जैसे किसी वास्तविक चर के फलन के मामले में लिया जाता है।

बुरी खबर यह है कि एक जटिल चर के कई कार्यों के लिए, कोई व्युत्पन्न बिल्कुल नहीं है, और आपको पता लगाना होगा भिन्न हैएक समारोह या कोई अन्य। और "पता लगाना" कि आपका दिल कैसा महसूस करता है, अतिरिक्त परेशानियों से जुड़ा है।

एक जटिल चर के एक समारोह पर विचार करें। इस फ़ंक्शन के अवकलनीय होने के लिए, यह आवश्यक और पर्याप्त है कि:

1) पहले क्रम के आंशिक व्युत्पन्न होने के लिए। इन नोटेशन के बारे में तुरंत भूल जाओ, क्योंकि एक जटिल चर के कार्य के सिद्धांत में, संकेतन का एक और संस्करण पारंपरिक रूप से उपयोग किया जाता है: .

2) तथाकथित को अंजाम देने के लिए कॉची-रीमैन की स्थिति:

केवल इस मामले में व्युत्पन्न मौजूद होगा!

उदाहरण 3

समाधानतीन क्रमिक चरणों में विघटित:

1) फलन के वास्तविक और काल्पनिक भाग ज्ञात कीजिए। पिछले उदाहरणों में इस कार्य का विश्लेषण किया गया था, इसलिए मैं इसे बिना किसी टिप्पणी के लिखूंगा:

तब से:

इस तरह:

समारोह का काल्पनिक हिस्सा है।

मैं एक और तकनीकी बिंदु पर ध्यान दूंगा: किस क्रम मेंवास्तविक और काल्पनिक भागों में शब्द लिखें? हां, मूल रूप से इससे कोई फर्क नहीं पड़ता। उदाहरण के लिए, वास्तविक भाग को इस प्रकार लिखा जा सकता है: , और काल्पनिक - इस तरह: .

2) आइए कॉची-रीमैन शर्तों की पूर्ति की जाँच करें। उनमें से दो.

आइए स्थिति की जांच करके शुरू करें। हम खोजें आंशिक अवकलज:

इस प्रकार, शर्त पूरी होती है।

निस्संदेह, अच्छी खबर यह है कि आंशिक डेरिवेटिव लगभग हमेशा बहुत सरल होते हैं।

हम दूसरी शर्त की पूर्ति की जाँच करते हैं:

यह वही निकला, लेकिन विपरीत संकेतों के साथ, यानी शर्त भी पूरी होती है।

कॉची-रीमैन की शर्तें संतुष्ट हैं, इसलिए, फ़ंक्शन अलग-अलग है।

3) फ़ंक्शन के व्युत्पन्न का पता लगाएं। व्युत्पन्न भी बहुत सरल है और सामान्य नियमों के अनुसार पाया जाता है:

विभेदन में काल्पनिक इकाई को स्थिर माना जाता है।

उत्तर: - असली हिस्सा काल्पनिक हिस्सा है।
कॉची-रीमैन की शर्तें पूरी होती हैं, .

व्युत्पत्ति खोजने के दो और तरीके हैं, बेशक उनका उपयोग कम बार किया जाता है, लेकिन जानकारी दूसरे पाठ को समझने के लिए उपयोगी होगी - एक जटिल चर के कार्य को कैसे खोजें?

व्युत्पन्न सूत्र का उपयोग करके पाया जा सकता है:

इस मामले में:

इस तरह

व्युत्क्रम समस्या को हल करना आवश्यक है - परिणामी अभिव्यक्ति में, आपको अलग करने की आवश्यकता है। ऐसा करने के लिए, शब्दों में और कोष्ठक से बाहर निकालना आवश्यक है:

रिवर्स एक्शन, जैसा कि कई लोगों ने देखा है, प्रदर्शन करना कुछ अधिक कठिन है, सत्यापन के लिए अभिव्यक्ति और ड्राफ्ट पर या मौखिक रूप से कोष्ठक को वापस खोलना हमेशा बेहतर होता है, यह सुनिश्चित करते हुए कि यह बिल्कुल ठीक हो जाएगा

व्युत्पन्न खोजने के लिए दर्पण सूत्र:

इस मामले में: , इसीलिए:

उदाहरण 4

फ़ंक्शन के वास्तविक और काल्पनिक भागों का निर्धारण करें . कॉची-रीमैन शर्तों की पूर्ति की जाँच करें। यदि कॉची-रीमैन की शर्तें पूरी होती हैं, तो फ़ंक्शन का व्युत्पन्न खोजें।

पाठ के अंत में एक संक्षिप्त समाधान और परिष्करण का अनुमानित नमूना।

क्या कॉची-रीमैन की स्थितियां हमेशा संतुष्ट रहती हैं? सैद्धांतिक रूप से, वे जितनी बार हैं उससे अधिक बार पूरी नहीं होती हैं। लेकिन व्यावहारिक उदाहरणों में, मुझे ऐसा कोई मामला याद नहीं है जहां उन्हें निष्पादित नहीं किया गया था =) इस प्रकार, यदि आपका आंशिक डेरिवेटिव "अभिसरण नहीं हुआ", तो बहुत अधिक संभावना के साथ हम कह सकते हैं कि आपने कहीं गलती की है।

आइए हमारे कार्यों को जटिल करें:

उदाहरण 5

फ़ंक्शन के वास्तविक और काल्पनिक भागों का निर्धारण करें . कॉची-रीमैन शर्तों की पूर्ति की जाँच करें। गणना

समाधान:समाधान एल्गोरिथ्म पूरी तरह से संरक्षित है, लेकिन अंत में एक नई सनक जोड़ी जाती है: एक बिंदु पर व्युत्पन्न खोजना। घन के लिए, आवश्यक सूत्र पहले ही प्राप्त किया जा चुका है:

आइए इस फ़ंक्शन के वास्तविक और काल्पनिक भागों को परिभाषित करें:

ध्यान और फिर ध्यान!

तब से:


इस तरह:
समारोह का असली हिस्सा है;
समारोह का काल्पनिक हिस्सा है।

दूसरी स्थिति की जाँच:

यह वही निकला, लेकिन विपरीत संकेतों के साथ, यानी शर्त भी पूरी होती है।

कॉची-रीमैन की शर्तें संतुष्ट हैं, इसलिए, फ़ंक्शन अलग-अलग है:

वांछित बिंदु पर व्युत्पन्न के मूल्य की गणना करें:

उत्तर:कॉची-रीमैन की शर्तें संतुष्ट हैं,

क्यूब्स के साथ कार्य आम हैं, इसलिए समेकित करने के लिए एक उदाहरण:

उदाहरण 6

फ़ंक्शन के वास्तविक और काल्पनिक भागों का निर्धारण करें . कॉची-रीमैन शर्तों की पूर्ति की जाँच करें। गणना करें।

पाठ के अंत में निर्णय और नमूना परिष्करण।

जटिल विश्लेषण के सिद्धांत में, एक जटिल तर्क के अन्य कार्यों को भी परिभाषित किया गया है: घातांक, साइन, कोसाइन, आदि। इन कार्यों में असामान्य और यहां तक ​​कि विचित्र गुण हैं - और यह वास्तव में दिलचस्प है! मैं वास्तव में आपको बताना चाहता हूं, लेकिन यहां, यह एक संदर्भ पुस्तक या पाठ्यपुस्तक नहीं, बल्कि एक समाधान के रूप में हुआ, इसलिए मैं कुछ सामान्य कार्यों के साथ उसी कार्य पर विचार करूंगा।

पहले तथाकथित . के बारे में यूलर सूत्र:

किसी के लिए भी वैधसंख्या, निम्नलिखित सूत्र मान्य हैं:

आप इसे संदर्भ के रूप में अपनी नोटबुक में कॉपी भी कर सकते हैं।

कड़ाई से बोलते हुए, केवल एक ही सूत्र है, लेकिन आमतौर पर सुविधा के लिए, वे संकेतक में माइनस के साथ एक विशेष मामला भी लिखते हैं। पैरामीटर के लिए एक अक्षर होना जरूरी नहीं है, यह एक जटिल अभिव्यक्ति, एक फ़ंक्शन हो सकता है, यह केवल महत्वपूर्ण है कि वे लेते हैं केवल मान्यमूल्य। दरअसल, हम इसे अभी देखेंगे:

उदाहरण 7

व्युत्पन्न खोजें।

समाधान:पार्टी की सामान्य रेखा अडिग रहती है - समारोह के वास्तविक और काल्पनिक भागों को अलग करना आवश्यक है। मैं एक विस्तृत समाधान दूंगा, और नीचे दिए गए प्रत्येक चरण पर टिप्पणी करूंगा:

तब से:

(1) "z" के लिए स्थानापन्न करें।

(2) प्रतिस्थापन के बाद वास्तविक और काल्पनिक भागों को अलग करना आवश्यक है घातांक में प्रथमप्रदर्शक। ऐसा करने के लिए, कोष्ठक खोलें।

(3) हम काल्पनिक इकाई को कोष्ठक से बाहर रखते हुए संकेतक के काल्पनिक भाग को समूहित करते हैं।

(4) शक्तियों के साथ स्कूल कार्रवाई का प्रयोग करें।

(5) गुणक के लिए, हम यूलर सूत्र का उपयोग करते हैं, जबकि ।

(6) परिणामस्वरूप हम कोष्ठक खोलते हैं:

समारोह का असली हिस्सा है;
समारोह का काल्पनिक हिस्सा है।

आगे की कार्रवाइयाँ मानक हैं, आइए कॉची-रीमैन शर्तों की पूर्ति की जाँच करें:

उदाहरण 9

फ़ंक्शन के वास्तविक और काल्पनिक भागों का निर्धारण करें . कॉची-रीमैन शर्तों की पूर्ति की जाँच करें। तो यह हो, हम व्युत्पन्न नहीं पाएंगे।

समाधान:समाधान एल्गोरिथ्म पिछले दो उदाहरणों के समान है, लेकिन बहुत महत्वपूर्ण बिंदु हैं, इसलिए मैं फिर से प्रारंभिक चरण पर चरण दर चरण टिप्पणी करूंगा:

तब से:

1) हम "z" के स्थान पर स्थानापन्न करते हैं।

(2) सबसे पहले, वास्तविक और काल्पनिक भागों का चयन करें साइनस के अंदर. ऐसा करने के लिए, कोष्ठक खोलें।

(3) हम सूत्र का उपयोग करते हैं, जबकि .

(4) प्रयोग करें अतिपरवलयिक कोज्या की समता: तथा अतिशयोक्तिपूर्ण साइन विषमता: . हाइपरबॉलिक्स, हालांकि इस दुनिया के नहीं, लेकिन कई मायनों में समान त्रिकोणमितीय कार्यों से मिलते जुलते हैं।

अंततः:
समारोह का असली हिस्सा है;
समारोह का काल्पनिक हिस्सा है।

ध्यान!ऋण चिह्न काल्पनिक भाग को दर्शाता है, और किसी भी स्थिति में हमें इसे खोना नहीं चाहिए! एक दृश्य चित्रण के लिए, ऊपर प्राप्त परिणाम को निम्नानुसार फिर से लिखा जा सकता है:

आइए कॉची-रीमैन शर्तों की पूर्ति की जाँच करें:

कॉची-रीमैन की शर्तें पूरी होती हैं।

उत्तर:कॉची-रीमैन की शर्तें संतुष्ट हैं।

कोसाइन, देवियों और सज्जनों के साथ, हम अपने आप समझते हैं:

उदाहरण 10

फ़ंक्शन के वास्तविक और काल्पनिक भागों का निर्धारण करें। कॉची-रीमैन शर्तों की पूर्ति की जाँच करें।

मैंने जानबूझकर अधिक जटिल उदाहरण उठाए, क्योंकि हर कोई खुली मूंगफली की तरह कुछ संभाल सकता है। उसी समय, अपना ध्यान प्रशिक्षित करें! पाठ के अंत में सरौता।

खैर, निष्कर्ष में, मैं एक और दिलचस्प उदाहरण पर विचार करूंगा जब जटिल तर्क हर में होगा। हम अभ्यास में एक-दो बार मिले, आइए कुछ सरल का विश्लेषण करें। ओह, मैं बूढ़ा हो रहा हूँ ...

उदाहरण 11

फ़ंक्शन के वास्तविक और काल्पनिक भागों का निर्धारण करें। कॉची-रीमैन शर्तों की पूर्ति की जाँच करें।

समाधान:फिर से, फ़ंक्शन के वास्तविक और काल्पनिक भागों को अलग करना आवश्यक है।
तो अगर

प्रश्न उठता है कि जब हर में "Z" हो तो क्या करें?

सब कुछ सरल है - मानक मदद करेगा संयुग्मी व्यंजक द्वारा अंश और हर को गुणा करने की विधि, यह पहले से ही पाठ के उदाहरणों में उपयोग किया जा चुका है डमी के लिए जटिल संख्या. आइए याद करते हैं स्कूल का फॉर्मूला। भाजक में हमारे पास पहले से है, इसलिए संयुग्मी व्यंजक होगा। इस प्रकार, आपको अंश और हर को इससे गुणा करना होगा:

11 एक जटिल चर के मूल कार्य

सम्मिश्र घातांक की परिभाषा याद कीजिए - . फिर

मैकलॉरिन श्रृंखला का विस्तार। इस श्रृंखला के अभिसरण की त्रिज्या +∞ है, जिसका अर्थ है कि जटिल घातांक पूरे जटिल तल पर विश्लेषणात्मक है और

(expक्स्प z)"=expक्स्प z; क्स्प 0=1. (2)

यहां पहली समानता इस प्रकार है, उदाहरण के लिए, एक शक्ति श्रृंखला के शब्द-दर-अवधि विभेदन पर प्रमेय से।

11.1 त्रिकोणमितीय और अतिपरवलयिक फलन

एक जटिल चर की ज्याएक समारोह कहा जाता है

एक जटिल चर की कोज्याएक समारोह है

जटिल चर की अतिपरवलयिक ज्याइस तरह परिभाषित किया गया है:

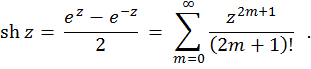
एक जटिल चर के अतिपरवलयिक कोज्या-- एक समारोह है

हम नए पेश किए गए कार्यों के कुछ गुणों पर ध्यान देते हैं।

ए।यदि x∈ , तो cos x, sin x, ch x, sh x∈ ।

बी।त्रिकोणमितीय और अतिपरवलयिक कार्यों के बीच निम्नलिखित संबंध है:

cos iz=ch z; sin iz=ish z, ch iz=cos z; शिज़ = इसिन्ज़।

B. मूल त्रिकोणमितीय और अतिपरवलयिक सर्वसमिकाएँ:

cos 2 z+sin 2 z=1; सी 2 जेड-श 2 जेड = 1।

मूल अतिशयोक्तिपूर्ण पहचान का प्रमाण।

जब त्रिकोणमितीय और अतिशयोक्तिपूर्ण कार्यों के बीच संबंध को ध्यान में रखा जाता है, तो मुख्य त्रिकोणमितीय पहचान ओनोनियन अतिपरवलयिक पहचान से होती है (संपत्ति बी देखें)

जी जोड़ सूत्र:

विशेष रूप से,

डी।त्रिकोणमितीय और अतिपरवलयिक फलनों के व्युत्पन्नों की गणना करने के लिए, किसी को घात श्रेणी के पद-दर-अवधि विभेदन पर प्रमेय लागू करना चाहिए। हम पाते हैं:

(cos z)"=-sin z; (sin z)"=cos z; (ch z)"=sh z; (sh z)"=ch z.

इ।फलन cos z, ch z सम हैं, जबकि फलन sin z, sh z विषम हैं।

जी. (आवधिकता)फलन e z आवर्त है जिसका आवर्त 2π i है। फलन cos z, sin z 2π की अवधि के साथ आवर्ती हैं, और फलन ch z, sh z 2πi की अवधि के साथ आवर्त हैं। इसके अलावा,

योग सूत्रों को लागू करने पर, हम प्राप्त करते हैं

वू. वास्तविक और काल्पनिक भागों में अपघटन:

यदि एक एकल-मूल्यवान विश्लेषणात्मक फलन f(z) किसी डोमेन D को डोमेन G पर विशेष रूप से मैप करता है, तो D को एकरूपता का डोमेन कहा जाता है।

तथा।डोमेन डी k =( x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .

सबूत। संबंध (5) का तात्पर्य है कि मानचित्रण क्स्प:D k → इंजेक्शन है। मान लीजिए w कोई शून्येतर सम्मिश्र संख्या है। फिर, समीकरणों को हल करना e x =|w| और ई iy =w/|w| वास्तविक चर x और y के साथ (हम आधे अंतराल से y चुनते हैं)