Eine lineare Funktion einer komplexen Variablen z ist eine Funktion der Form wobei a und 6 komplexe Zahlen erhalten und a Φ 0. Die lineare Funktion ist für alle Werte der unabhängigen Variablen z definiert, ist einwertig und da die Umkehrfunktion ebenfalls einwertig ist, in der gesamten Ebene z einwertig. Eine lineare Funktion ist in der gesamten komplexen Ebene analytisch, und ihre Ableitung, also die auf sie durchgeführte Abbildung, ist in der gesamten Ebene konform. Eine gebrochen-lineare Funktion ist eine Funktion der Form - gegebene komplexe Zahlen, und die gebrochen-lineare Funktion ist für alle Werte der unabhängigen Variablen zy außer z = - | definiert, ist einwertig und, da die Umkehrfunktion Elementare Funktionen einer komplexen Variablen Fraktionierte rationale Funktionen Potenzgesetze Exponentialfunktionsfunktion Logarithmische Funktion Trigonometrische und hyperbolische Funktionen sind einwertig, univalent in der gesamten komplexen Ebene, mit Ausnahme des Punktes z = - In diesem Bereich ist Funktion (3) analytisch und seine Ableitung ist daher konform. Erweitern wir die Definition der Funktion (3) um den Punkt z = - \, setzen wir £) = oo, und weisen wir den Punkt z (oo) = dem Punkt im Unendlichen w = oo zu. Dann ist die lineare Bruchfunktion einwertig in der erweiterten komplexen Ebene z. Beispiel 1. Betrachten Sie eine linear-gebrochene Funktion Aus der Gleichheit folgt, dass die Moduli der komplexen Zahlen r und u durch die Beziehung zusammenhängen und diese Zahlen selbst auf den Strahlen liegen, die vom Punkt O ausgehen und symmetrisch um die reelle Achse sind. Insbesondere die Punkte des Einheitskreises |z | = 1 gehe zu Punkten des Einheitskreises L = 1. In diesem Fall wird einer komplexen Zahl eine konjugierte Zahl zugeordnet (Abb. 11). Beachten Sie auch, dass die Funktion r = -g den Punkt im Unendlichen r - oo auf den Nullpunkt r - 0 abbildet. 2.2. Potenzfunktion Potenzfunktion wobei n eine natürliche Zahl ist, analytisch in der gesamten komplexen Ebene; seine Ableitung = nzn ~] für n> 1 ist in allen Punkten außer z = 0 von Null verschieden. Schreiben wir w und z in Exponentialform in Formel (4), erhalten wir aus Formel (5), dass die komplexen Zahlen Z \ und z2 mit wobei k eine ganze Zahl ist, gehe zu einem Punkt w. Daher ist für n > 1 die Abbildung (4) auf der z-Ebene nicht univalent. Das einfachste Beispiel für einen Bereich, in dem die Abbildung ry = zn univalent ist, ist der Sektor, in dem a eine beliebige reelle Zahl ist. Im Bereich (7) ist die Abbildung (4) konform. - mehrwertig, da man für jede komplexe Zahl z = r1 in Φ 0 n verschiedene komplexe Zahlen angeben kann, deren n-ter Grad gleich z ist: Man beachte, dass ein Polynom vom Grad n in einer komplexen Variablen z eine Funktion mit gegeben ist komplexe Zahlen außerdem ao Φ 0. Ein Polynom beliebigen Grades ist eine analytische Funktion auf der gesamten komplexen Ebene. 2.3. Bruchrationale Funktion Eine gebrochenrationale Funktion ist eine Funktion der Form wobei) sind Polynome einer komplexen Variablen z. Eine gebrochene rationale Funktion ist in der gesamten Ebene analytisch, mit Ausnahme der Punkte, an denen der Nenner Q (z) verschwindet. Beispiel 3. Die Zhukovskii-Funktion ist in der gesamten z-Ebene analytisch, mit Ausnahme des Punktes z = 0. Lassen Sie uns die Bedingungen für den Bereich der komplexen Ebene herausfinden, unter denen die in diesem Bereich betrachtete Zhukovskii-Funktion univalent ist. M Die Punkte Z) und zj seien durch Funktion (8) auf einen Punkt gebracht. Für die Einwertigkeit der Schukowski-Funktion ist es also notwendig und ausreichend, die Bedingung zu erfüllen Ein Beispiel für ein Gebiet, das die Einvalenzbedingung (9) erfüllt, ist das Äußere des Kreises | > 1. Da die Ableitung der Zhukovsky-Funktion Elementare Funktionen einer komplexen Variablen Fractional rationale Funktionen Potenzfunktion Exponentialfunktion Logarithmische Funktion trigonometrische und hyperbolische Funktionen außer in Punkten überall von Null verschieden sind, ist die von dieser Funktion durchgeführte Abbildung der Region konform (Abb. 13). Beachten Sie, dass das Innere der Einheitsscheibe | I auch der Einvalenzbereich der Schukowski-Funktion ist. Reis. 13 2.4. Die Exponentialfunktion Die Exponentialfunktion ez ist für jede komplexe Zahl z = x + zy wie folgt definiert: Für x = 0 erhalten wir die Eulersche Formel: Beschreiben wir die Haupteigenschaften der Exponentialfunktion: 1. Für reelle z gilt dies Definition stimmt mit der üblichen überein. Dies kann direkt durch Setzen von y = 0 überprüft werden. Wir setzen 4. Die Funktion ez ist periodisch mit einer imaginären Hauptperiode 2xi. In der Tat, für jede ganze Zahl k Auf der anderen Seite, wenn dann aus Definition (10) folgt, woraus es folgt, oder wo n eine ganze Zahl ist. Der Streifen enthält kein einziges Paar von Punkten, die durch die Beziehung (12) verbunden sind, daher folgt aus der durchgeführten Studie, dass die Abbildung w = e " im Streifen eine Linie ist (Abb. 14). Als Ableitung ist dies Abbildung ist konform Bemerkung Funktion rg ist in jedem Streifen univalent 2.5 Logarithmische Funktion Aus der Gleichung wo gegeben ist die Unbekannte, erhalten wir daher Die Funktion, die Inverse der Funktion ist für jeden definiert und wird durch die Formel dargestellt wobei This mehrwertige Funktion heißt logarithmisch und wird wie folgt bezeichnet: wird bezeichnet durch Dann erhält man Formel 2 für Ln z. 6. Trigonometrische und hyperbolische Funktionen Aus der Eulerschen Formel (11) für reelles y erhalten wir aus wobei Wir definieren die trigonometrischen Funktionen sin z und cos z für jede komplexe Zahl z mit den folgenden Formeln: Sinus und Kosinus eines komplexen Arguments haben interessante Eigenschaften. Lassen Sie uns die wichtigsten auflisten. Funktionen sinz und cos z: 1) für reelle z-x stimmen mit den üblichen Sinus und Cosinus überein; 2) sind auf der gesamten komplexen Ebene analytisch; 3) befolgen Sie die üblichen Differenzierungsformeln: 4) periodisch mit einer Periode von 2m; 5) sin z ist eine ungerade Funktion und cos z ist gerade; 6) die üblichen trigonometrischen Beziehungen bleiben erhalten. Alle aufgeführten Eigenschaften lassen sich leicht aus den Formeln (15) ermitteln. Die Funktionen tgz und ctgz im komplexen Bereich werden durch die Formeln und hyperbolische Funktionen durch die Formeln definiert "Hyperbolische Funktionen sind eng mit trigonometrischen Funktionen verwandt. Dieser Zusammenhang wird durch die folgenden Gleichungen ausgedrückt: Der Sinus und der Kosinus eines komplexen Arguments haben eine weitere wichtige Eigenschaft: auf der komplexen Ebene |\ nehmen sie beliebig große positive an. Mit den Eigenschaften 6 und den Formeln (18) erhalten wir: wir haben Beispiel 4. Es ist leicht zu überprüfen, dass -4 Tatsächlich ,

Komplexe variable Funktionen.
Differenzierung von Funktionen einer komplexen Variablen.

Dieser Artikel eröffnet eine Reihe von Lektionen, in denen ich typische Probleme im Zusammenhang mit der Theorie der Funktionen einer komplexen Variablen betrachte. Um die Beispiele erfolgreich zu meistern, müssen Sie über Grundkenntnisse komplexer Zahlen verfügen. Um das Material zu festigen und zu wiederholen, besuchen Sie einfach die Seite. Sie benötigen auch Fähigkeiten, um zu finden partielle Ableitungen zweiter Ordnung... Hier sind sie, diese partiellen Ableitungen ... selbst jetzt war ich selbst ein wenig überrascht, wie oft sie vorkommen ...

Das Thema, das wir zu analysieren beginnen, ist nicht besonders schwierig, und bei Funktionen einer komplexen Variablen ist im Prinzip alles klar und zugänglich. Hauptsache man hält sich an die Grundregel, die ich empirisch hergeleitet habe. Weiter lesen!

Komplexes variables Funktionskonzept

Lassen Sie uns zunächst unser Wissen über die Schulfunktion einer Variablen auffrischen:

Einzelvariable Funktion Ist eine Regel, nach der jedem Wert der unabhängigen Variablen (aus dem Definitionsbereich) ein und nur ein Funktionswert entspricht. Natürlich sind X und Y reelle Zahlen.

Im komplexen Fall wird die funktionale Abhängigkeit auf die gleiche Weise festgelegt:

Einwertige Funktion einer komplexen Variablen- das ist die Regel, nach der alle ein integriertes der Wert der unabhängigen Variablen (aus der Domäne) entspricht eins und nur einem Komplex Funktionswert. Theoretisch werden auch mehrwertige und einige andere Arten von Funktionen betrachtet, aber der Einfachheit halber werde ich mich auf eine Definition konzentrieren.

Was ist der Unterschied zwischen einer komplexen Variablenfunktion?

Der Hauptunterschied: Die Zahlen sind komplex. Ich bin nicht ironisch. Von solchen Fragen verfallen sie oft in einen Stumpfsinn, am Ende des Artikels erzähle ich Ihnen eine lustige Geschichte. Im Unterricht Komplexe Zahlen für Dummies wir haben eine komplexe Zahl in der Form betrachtet. Seitdem ist der Buchstabe "z" geworden Variable, dann werden wir es wie folgt bezeichnen:, während "x" und "game" unterschiedlich sein können gültig Werte. Grob gesagt hängt die Funktion einer komplexen Variablen von Variablen ab, die "normale" Werte annehmen. Aus dieser Tatsache folgt logischerweise folgender Punkt:

Die Funktion einer komplexen Variablen kann wie folgt geschrieben werden:
, wobei und zwei Funktionen von zwei sind gültig Variablen.

Die Funktion heißt echter teil Funktionen.
Die Funktion heißt imaginärer Teil Funktionen.

Das heißt, die Funktion einer komplexen Variablen hängt von zwei reellen Funktionen und ab. Um alles abschließend zu verdeutlichen, betrachten Sie praktische Beispiele:

Beispiel 1

Lösung: Die unabhängige Variable "z" wird, wie Sie sich erinnern, geschrieben als:

(1) Die ursprüngliche Funktion wurde ersetzt.

(2) Für den ersten Term wurde die abgekürzte Multiplikationsformel verwendet. Im Begriff wurden Klammern geöffnet.

(3) Sorgfältig quadriert, nicht zu vergessen

(4) Neuordnung der Terme: zuerst Terme umschreiben in der es keine imaginäre Einheit gibt(erste Gruppe), dann die Begriffe, wo sie sich befinden (zweite Gruppe). Es ist zu beachten, dass es nicht notwendig ist, die Begriffe zu mischen, und diese Phase kann übersprungen werden (tatsächlich nach mündlicher Ausführung).

(5) Für die zweite Gruppe nehmen wir sie aus den Klammern.

Als Ergebnis stellte sich heraus, dass unsere Funktion in der Form dargestellt wird

Antworten:
- der eigentliche Teil der Funktion.
- der Imaginärteil der Funktion.

Was sind das für Funktionen? Die gewöhnlichsten Funktionen zweier Variablen, aus denen man so beliebte partielle Ableitungen... Ohne Gnade - wir werden finden. Aber etwas später.

Kurz gesagt lässt sich der Algorithmus des gelösten Problems wie folgt schreiben: in die Originalfunktion einsetzen, vereinfachen und alle Terme in zwei Gruppen teilen - ohne Imaginäreinheit (Realteil) und mit Imaginäreinheit (Imaginärteil).

Beispiel 2

Finden Sie Real- und Imaginärteil einer Funktion

Dies ist ein Beispiel für eine Do-it-yourself-Lösung. Bevor Sie Ihre Spielsteine ​​in einem komplexen Flugzeug in die Schlacht werfen, möchte ich Ihnen die wichtigsten Ratschläge zu diesem Thema geben:

SEIEN SIE AUFMERKSAM! Sie müssen natürlich überall aufmerksam sein, aber bei komplexen Zahlen sollten Sie so aufmerksam sein wie nie zuvor! Denken Sie daran, die Klammern vorsichtig zu öffnen, nichts zu verlieren. Nach meinen Beobachtungen ist der häufigste Fehler der Verlust eines Schildes. Beeil dich nicht!

Komplette Lösung und Antwort am Ende des Tutorials.

Jetzt der Würfel. Mit der Formel für die reduzierte Multiplikation erhalten wir:
.

Formeln sind in der Praxis sehr praktisch, da sie den Lösungsprozess erheblich beschleunigen.

Differenzierung von Funktionen einer komplexen Variablen.

Ich habe zwei Neuigkeiten: gute und schlechte. Ich fange mit einem guten an. Für eine Funktion einer komplexen Variablen gelten die Ableitungsregeln und die Ableitungstabelle elementarer Funktionen. Die Ableitung erfolgt also wie bei einer reellen Variablenfunktion.

Die schlechte Nachricht ist, dass für viele Funktionen einer komplexen Variablen die Ableitung überhaupt nicht existiert und Sie herausfinden müssen, differenzierbar diese oder jene Funktion. Und "herauszufinden", wie sich dein Herz anfühlt, ist mit zusätzlichen Problemen verbunden.

Betrachten Sie eine komplexe variable Funktion. Damit diese Funktion differenzierbar ist, ist es notwendig und ausreichend:

1) Für die Existenz partieller Ableitungen erster Ordnung. Vergessen Sie diese Bezeichnungen gleich, denn in der Theorie der Funktion einer komplexen Variablen wird traditionell eine andere Schreibweise verwendet: .

2) Zur Durchführung der sogenannten Cauchy-Riemann-Bedingungen:

Nur in diesem Fall existiert die Ableitung!

Beispiel 3

Lösung zerfällt in drei aufeinanderfolgende Phasen:

1) Finden Sie den Real- und Imaginärteil der Funktion. Diese Aufgabe wurde in den vorherigen Beispielen analysiert, daher werde ich sie ohne Kommentare aufschreiben:

Seit damals:

Auf diese Weise:

- der Imaginärteil der Funktion.

Ich werde auf einen weiteren technischen Punkt eingehen: in welcher Reihenfolge die Terme im Real- und Imaginärteil aufschreiben? Ja, im Prinzip kein Unterschied. Der Realteil kann zum Beispiel so geschrieben werden: , und imaginär - wie folgt:.

2) Prüfen wir die Erfüllung der Cauchy-Riemann-Bedingungen. Es gibt zwei davon.

Beginnen wir mit der Überprüfung der Bedingung. Finden partielle Ableitungen:

Damit ist die Bedingung erfüllt.

Die gute Nachricht ist zweifellos, dass partielle Ableitungen fast immer sehr einfach sind.

Wir prüfen die Erfüllung der zweiten Bedingung:

Es stellte sich das gleiche heraus, jedoch mit entgegengesetzten Vorzeichen, dh die Bedingung ist auch erfüllt.

Die Cauchy-Riemann-Bedingungen sind erfüllt, daher ist die Funktion differenzierbar.

3) Finden Sie die Ableitung der Funktion. Auch die Ableitung ist sehr einfach und ergibt sich nach den üblichen Regeln:

Die imaginäre Einheit bei der Differentiation wird als Konstante betrachtet.

Antworten: - echter Teil, Ist der Imaginärteil.
Die Cauchy-Riemann-Bedingungen sind erfüllt.

Es gibt zwei weitere Möglichkeiten, die Ableitung zu finden, sie werden natürlich seltener verwendet, aber die Informationen werden zum Verständnis der zweiten Lektion nützlich sein - Wie finde ich die Funktion einer komplexen Variablen?

Die Ableitung kann durch die Formel gefunden werden:

In diesem Fall:

Auf diese Weise

Wir müssen das inverse Problem lösen - im resultierenden Ausdruck müssen Sie isolieren. Dazu ist es in den AGB notwendig und aus der Klammer zu setzen:

Der umgekehrte Vorgang ist, wie viele bemerkt haben, etwas schwieriger durchzuführen, zur Überprüfung ist es immer besser, einen Ausdruck zu nehmen und auf einem Entwurf oder mündlich die Klammern zu öffnen, um sicherzustellen, dass er genau ausfällt

Spiegelformel zum Finden der Ableitung:

In diesem Fall: , deshalb:

Beispiel 4

Bestimme Real- und Imaginärteil einer Funktion ... Prüfen Sie die Erfüllung der Cauchy-Riemann-Bedingungen. Wenn die Cauchy-Riemann-Bedingungen erfüllt sind, bestimme die Ableitung der Funktion.

Eine kurze Lösung und ein grobes Finishing-Beispiel am Ende des Tutorials.

Sind die Cauchy-Riemann-Bedingungen immer erfüllt? Theoretisch werden sie häufiger nicht ausgeführt, als sie es sind. Aber in praktischen Beispielen erinnere ich mich nicht an einen Fall, in dem sie nicht ausgeführt wurden =) Wenn also Ihre partiellen Ableitungen „nicht übereinstimmten“, können Sie mit sehr hoher Wahrscheinlichkeit sagen, dass Sie irgendwo einen Fehler gemacht haben.

Verkomplizieren wir unsere Funktionen:

Beispiel 5

Bestimme Real- und Imaginärteil einer Funktion ... Prüfen Sie die Erfüllung der Cauchy-Riemann-Bedingungen. Berechnung

Lösung: Der Lösungsalgorithmus bleibt vollständig erhalten, aber am Ende wird eine neue Modeerscheinung hinzugefügt: das Finden der Ableitung an dem Punkt. Für den Würfel wurde die erforderliche Formel bereits abgeleitet:

Lassen Sie uns den Real- und Imaginärteil dieser Funktion definieren:

Achtung und nochmal Aufmerksamkeit!

Seit damals:


Auf diese Weise:
- der Realteil der Funktion;
- der Imaginärteil der Funktion.

Überprüfung der zweiten Bedingung:

Es stellte sich das gleiche heraus, jedoch mit entgegengesetzten Vorzeichen, dh die Bedingung ist auch erfüllt.

Die Cauchy-Riemann-Bedingungen sind erfüllt, daher ist die Funktion differenzierbar:

Berechnen wir den Wert der Ableitung an der erforderlichen Stelle:

Antworten:,, die Cauchy-Riemann-Bedingungen sind erfüllt,

Funktionen mit Würfeln sind üblich, daher ein Beispiel zur Verdeutlichung:

Beispiel 6

Bestimme Real- und Imaginärteil einer Funktion ... Prüfen Sie die Erfüllung der Cauchy-Riemann-Bedingungen. Berechnung.

Lösungs- und Musterabschluss am Ende der Lektion.

In der Theorie der komplexen Analysis werden auch andere Funktionen eines komplexen Arguments definiert: Exponent, Sinus, Cosinus usw. Diese Funktionen haben ungewöhnliche und sogar skurrile Eigenschaften – und das ist wirklich interessant! Ich möchte Ihnen sehr viel erzählen, aber hier ist es einfach so passiert, kein Nachschlagewerk oder Lehrbuch, sondern ein Löser, also werde ich das gleiche Problem mit einigen gängigen Funktionen betrachten.

Zunächst zu den sogenannten Eulersche Formeln:

Für jeden tatsächlich Nummer gelten folgende Formeln:

Sie können es auch als Referenzmaterial in einem Notizbuch umschreiben.

Streng genommen gibt es nur eine Formel, aber normalerweise schreiben sie der Einfachheit halber auch einen Sonderfall mit einem Minus im Indikator. Der Parameter muss kein einsamer Buchstabe sein, ein komplexer Ausdruck, eine Funktion kann als Funktion fungieren, wichtig ist nur, dass sie akzeptieren nur gültig Werte. Eigentlich werden wir es gleich sehen:

Beispiel 7

Finden Sie die Ableitung.

Lösung: Die allgemeine Linie der Partei bleibt unerschütterlich - es ist notwendig, die realen und imaginären Teile der Funktion herauszuheben. Ich werde eine detaillierte Lösung geben, und unten werde ich jeden Schritt kommentieren:

Seit damals:

(1) Ersetzen Sie "z".

(2) Nach der Ersetzung müssen Sie den Real- und Imaginärteil auswählen zuerst im Indikator Aussteller. Öffnen Sie dazu die Klammern.

(3) Wir gruppieren den Imaginärteil des Indikators, indem wir die imaginäre Einheit aus den Klammern nehmen.

(4) Wir nutzen Schulaktionen mit Abschlüssen.

(5) Für den Faktor verwenden wir die Euler-Formel, while.

(6) Erweitern Sie die Klammern, was zu Folgendem führt:

- der Realteil der Funktion;
- der Imaginärteil der Funktion.

Weitere Maßnahmen sind Standard, prüfen Sie die Erfüllung der Cauchy-Riemann-Bedingungen:

Beispiel 9

Bestimme Real- und Imaginärteil einer Funktion ... Prüfen Sie die Erfüllung der Cauchy-Riemann-Bedingungen. Wir werden das Derivat nicht finden, sei es so.

Lösung: Der Lösungsalgorithmus ist den beiden vorherigen Beispielen sehr ähnlich, aber es gibt sehr wichtige Punkte, daher werde ich die Anfangsphase Schritt für Schritt noch einmal kommentieren:

Seit damals:

1) Ersetzen Sie "z".

(2) Wählen Sie zuerst den Real- und Imaginärteil aus innerer Sinus... Dazu öffnen wir die Klammern.

(3) Wir verwenden die Formel, während .

(4) Wir verwenden Parität des hyperbolischen Kosinus: und ungerader hyperbolischer Sinus:. Hyperbeln, obwohl nicht von dieser Welt, ähneln in vielerlei Hinsicht ähnlichen trigonometrischen Funktionen.

Zusammenfassend:
- der Realteil der Funktion;
- der Imaginärteil der Funktion.

Beachtung! Das Minuszeichen bezieht sich auf den Imaginärteil, und wir verlieren ihn in keiner Weise! Zur besseren Veranschaulichung kann das oben erhaltene Ergebnis wie folgt umgeschrieben werden:

Prüfen wir die Erfüllung der Cauchy-Riemann-Bedingungen:

Die Cauchy-Riemann-Bedingungen sind erfüllt.

Antworten:,, die Cauchy-Riemann-Bedingungen sind erfüllt.

Mit dem Kosinus, meine Damen und Herren, finden wir es selbst heraus:

Beispiel 10

Bestimmen Sie den Real- und Imaginärteil der Funktion. Prüfen Sie die Erfüllung der Cauchy-Riemann-Bedingungen.

Ich habe bewusst kompliziertere Beispiele gewählt, weil jeder mit so etwas wie geschälten Erdnüssen zurechtkommt. Gleichzeitig schulst du deine Aufmerksamkeit! Nussknacker am Ende der Lektion.

Abschließend möchte ich noch ein weiteres interessantes Beispiel betrachten, wenn ein komplexes Argument im Nenner steht. Ich habe mich in der Praxis ein paar Mal getroffen, lassen Sie uns etwas Einfaches analysieren. Äh, ich werde alt...

Beispiel 11

Bestimmen Sie den Real- und Imaginärteil der Funktion. Prüfen Sie die Erfüllung der Cauchy-Riemann-Bedingungen.

Lösung: Auch hier ist es notwendig, den Real- und den Imaginärteil der Funktion zu trennen.
Wenn, dann

Es stellt sich die Frage, was tun, wenn „z“ im Nenner steht?

Alles ist naiv - der Standard hilft Trick, Zähler und Nenner mit dem konjugierten Ausdruck zu multiplizieren, es wurde bereits in den Beispielen der Lektion verwendet Komplexe Zahlen für Dummies... Wir erinnern uns an die Schulformel. Wir haben es bereits im Nenner, was bedeutet, dass es ein konjugierter Ausdruck ist. Daher müssen Sie Zähler und Nenner multiplizieren mit:

11 Grundfunktionen einer komplexen Variablen

Erinnern wir uns an die Definition des komplexen Exponenten -. Dann

Erweiterung der Maclaurin-Reihe. Der Konvergenzradius dieser Reihe ist + ∞, was bedeutet, dass der komplexe Exponent auf der gesamten komplexen Ebene analytisch ist und

(exp z) "= exp z; exp 0 = 1. (2)

Die erste Gleichheit folgt hier beispielsweise aus dem Term-für-Term-Differenzierungssatz für eine Potenzreihe.

11.1 Trigonometrische und hyperbolische Funktionen

Sinus komplexe Variable die Funktion heißt

Kosinus einer komplexen Variablen es gibt eine funktion

Hyperbolischer Sinus einer komplexen Variablen so definiert:

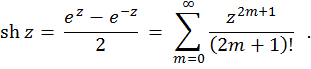
Hyperbolischer Kosinus einer komplexen Variablen ist eine Funktion

Beachten wir einige Eigenschaften der neu eingeführten Funktionen.

A. Wenn x∈ ℝ, dann cos x, sin x, ch x, sh x∈ ℝ.

B. Zwischen trigonometrischen und hyperbolischen Funktionen besteht folgender Zusammenhang:

cosiz = chz; sin iz = ish z, ch iz = cos z; shiz = isin z.

B. Grundlegende trigonometrische und hyperbolische Identitäten:

cos 2 z + sin 2 z = 1; ch 2 z-sch 2 z = 1.

Beweis der hyperbolischen Hauptidentität.

Die trigonometrische Hauptidentität folgt aus der hyperbolischen Hauptidentität unter Berücksichtigung des Zusammenhangs zwischen trigonometrischen und hyperbolischen Funktionen (siehe Eigenschaft B)

g Additionsformeln:

Insbesondere,

D. Um die Ableitungen trigonometrischer und hyperbolischer Funktionen zu berechnen, sollte man den Satz über die Term-für-Term-Differenzierung einer Potenzreihe anwenden. Wir bekommen:

(cos z) "= - sin z; (sin z)" = cos z; (ch z) "= sh z; (sh z)" = ch z.

E. Die Funktionen cos z, ch z sind gerade und die Funktionen sin z, sh z ungerade.

G. (Periodizität) Die Funktion e z ist periodisch mit einer Periode von 2π i. Die Funktionen cos z, sin z sind periodisch mit einer Periode von 2π und die Funktionen ch z, sh z sind periodisch mit einer Periode von 2πi. Außerdem,

Mit den Summenformeln erhalten wir

Z. Zerlegung in Real- und Imaginärteil:

Wenn eine einwertige analytische Funktion f (z) bijektiv ein Gebiet D auf ein Gebiet G abbildet, dann wird D ein Gebiet der Schlichtheit genannt.

UND. Bereich D k = (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .

Nachweisen. Aus Beziehung (5) folgt, dass die Abbildung exp: D k → ℂ injektiv ist. Sei w eine beliebige komplexe Zahl ungleich Null. Dann löst man die Gleichungen e x = |w | und e iy = w / |w | mit reellen Variablen x und y (wähle y aus einem Halbintervall)