Določilne lastnosti. Znižanje vrstnega reda determinante

nekaj številko izračunano po določenem pravilu in imenovano determinanta.

Potreba po predstavitvi koncepta determinanta - številke karakteriziranje kvadratni matrika naročila n , je tesno povezana z rešitvijo sistemov linearnih algebraičnih enačb.

Determinanta matrike A označili bomo: | A| ali D.

Determinanta matrike prvega redaA = (a 11) se imenuje element a enajst . Na primer, za A= (-4) imamo | A| = -4.

Določevalec matrike drugega reda poklical številko določeno s formulo

|A| = .

Na primer, | A| = .

Z besedami lahko to pravilo zapišemo takole: s svojim znakom morate vzeti produkt povezanih elementov glavna diagonala, in produkti elementov, povezanih z oglišči trikotnikov, za katere osnova vzporedna z glavno diagonalo... Z nasprotnim predznakom vzamemo podobne izdelke, le glede na stransko diagonalo.

na primer

Določanje determinante matrike n Ne bomo dali th vrstnega reda, ampak samo pokazali način za njegovo iskanje.

Nadalje, namesto besed determinanta matrike n-to naročilo recimo determinanta n-to naročilo... Predstavimo nove koncepte.

Podano kvadratno matriko n th red.

ManjšiM ij element a ij matrike A poklical determinanta (n-1) vrstni red, pridobljen iz matrike A brisanje jaz-to vrstico in j th stolpec.

Algebraično dopolnilo А ij elementa а ij matrike А imenujemo njegov minor, vzet s predznakom (-1) i + j:

A ij = (-1) i + j M ij,

tiste. algebraično dopolnilo bodisi sovpada s svojim minorom, ko je vsota številk vrstic in stolpcev sodo število, ali se od njega razlikuje po predznaku, če je vsota številk vrstic in stolpcev liho število.

Na primer za elemente a 11 in a 12 matric A = mladoletne osebe

M 11 = A 11 = ,

M 12 = ,

a A 12 = (-1) 1+2 M 12 = -8.

Izrek (o razširitvi determinante) . Določevalec kvadratne matrike je enak vsoti produktov elementov katere koli vrstice (stolpca) z njihovimi algebrskimi komplementi, t.j.

|A| = a i1 A i1 + a i2 A i2 + ... + a v A v,
za vsakogar jaz = 1, 2, …, n

|A| = a 1j A 1j + a 2j A 2j + ... + a nj A nj,

za vsakogar j = 1, 2, …, n

Prva formula se imenuje jaz-ta vrstica, in drugi je razširitev determinante v elemente j th stolpec.

Preprosto je razumeti, da s pomočjo teh formul katera koli determinanta n-narednost se lahko zmanjša na vsoto determinant, katerih vrstni red bo 1 manj itd. dokler ne pridemo do determinant 3. ali 2. reda, katerih izračun ni več težak.

Za iskanje determinante lahko uporabimo naslednje osnovne lastnosti:

1. Če je katera koli vrstica (ali stolpec) determinante sestavljena iz ničel, je determinanta sama enaka nič.

2. Pri menjavi poljubnih dveh vrstic (ali dveh stolpcev) se determinanta pomnoži z -1.

3. Determinanta z dvema enakima ali sorazmernima vrsticama (ali stolpcima) je enaka nič.

4. Skupni faktor elementov katere koli vrstice (ali stolpca) je mogoče vzeti iz determinante.

5. Vrednost determinante se ne bo spremenila, če zamenjate vse vrstice in stolpce.

6. Vrednost determinante se ne bo spremenila, če v eno od vrstic (ali v enega od stolpcev) dodamo še eno vrstico (stolpec), pomnoženo s poljubnim številom.

7. Vsota produktov elementov katere koli vrstice (ali stolpca) matrike z algebrskimi dopolnitvami elementov druge vrstice (stolpca) te matrike je enaka nič.

8. Določnik produkta dveh kvadratnih matrik je enak zmnožku njunih determinant.

Uvedba pojma determinante matrike nam omogoča, da definiramo še eno dejanje z matrikami – iskanje inverzne matrike.

Za vsako ničelno število obstaja obratno število, tako da zmnožek teh števil daje eno. Obstaja tudi takšen koncept za kvadratne matrike.

Matrika A-1 se imenuje vzvratno proti kvadratni matrika Ače pomnožimo to matriko s podano tako na desni kot na levi strani matriko identitete, tj.

A× A -1 = A-1 × A= E.

Iz definicije izhaja, da ima le kvadratna matrika obratno; v tem primeru bo inverzna matrika kvadrat enakega reda. Vendar nima vsaka kvadratna matrika svoje inverzne vrednosti.

ALGEBRASKI DODATKI IN MINORI

Imejmo determinanto tretjega reda: .

Manjši ki ustreza temu elementu a ij determinanta tretjega reda, se imenuje determinanta drugega reda, ki jo dobimo iz danega tako, da izbrišemo vrstico in stolpec, na presečišču katerih stoji dani element, t.j. jaz-to vrstico in j stolpec. Mladoletniki, ki ustrezajo danemu elementu a ij bo označevalo M ij.

Na primer, manjša M 12 ki ustreza elementu a 12, bo determinanta 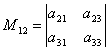, ki ga dobimo tako, da iz dane determinante izbrišemo 1. vrstico in 2. stolpec.

Tako formula, ki definira determinanto tretjega reda, kaže, da je ta determinanta enaka vsoti zmnožkov elementov 1. vrstice z ustreznimi minorji; v tem primeru minor, ki ustreza elementu a 12, vzeto z znakom "-", t.j. to lahko napišemo

Podobno lahko uvedemo definicije minorov za determinante drugega in višjega reda.

Predstavimo še en koncept.

Algebrsko dopolnilo element a ij determinanta se imenuje njegov minor M ij pomnoženo z (–1) i + j.

Algebraično dopolnilo elementa a ij označeno A ij.

Iz definicije dobimo, da je povezava med algebraičnim komplementom elementa in njegovim minorjem izražena z enakostjo A ij= (–1) i + j M ij.

na primer

Primer. Podan je determinant. Najti A 13, A 21, A 32.

Preprosto je videti, da lahko z uporabo algebrskih komplementov elementov formulo (1) zapišemo v obliki:

Podobno kot pri tej formuli lahko dobite razgradnjo determinante na elemente katere koli vrstice ali stolpca.

Na primer, faktoring determinante z elementi 2. vrstice lahko dobimo na naslednji način. Glede na lastnost 2 determinante imamo:

Razširimo nastalo determinanto za elemente prve vrstice.

.

(2)

Od tod od determinante drugega reda v formuli (2) so minori elementov a 21, 22, 23... Tako, t.j. dobili smo razgradnjo determinante glede na elemente 2. vrstice.

Podobno lahko dobite faktorizacijo determinante glede na elemente tretje vrstice. Z lastnostjo 1 determinant (o prenosu) lahko pokažemo, da podobne razširitve veljajo tudi za razširitev v smislu elementov stolpca.

Tako je naslednji izrek resničen.

Izrek (o razširitvi determinante v dani vrstici ali stolpcu). Določitev je enaka vsoti produktov elementov katere koli vrstice (ali stolpca) z njihovimi algebrskimi dopolnitvami.

Vse našteto velja tudi za determinante katerega koli višjega reda.

Primeri.

INVERZNA MATRICA

Koncept inverzne matrike je uveden samo za kvadratne matrike.

Če A Torej je kvadratna matrika vzvratno zanjo se matrika imenuje matrika, označena A -1 in izpolnitev pogoja. (Ta definicija je uvedena po analogiji z množenjem številk)

LASTNOST 1. Vrednost determinante se ne spremeni, če vse njene vrstice nadomestimo s stolpci in vsako vrstico nadomestimo s stolpcem z isto številko, tj.

LASTNOST 2. Permutacija dveh stolpcev ali dveh vrstic determinante je enakovredna pomnoženju z -1. na primer

.

LASTNOST 3. Če ima determinanta dva enaka stolpca ali dve enaki vrstici, je enaka nič.

LASTNOST 4. Množenje vseh elementov enega stolpca ali ene vrstice determinante s katerim koli številom k je enakovredno množenju determinante s tem številom k. na primer

.

LASTNOST 5. Če so vsi elementi nekega stolpca ali vrstice enaki nič, je determinanta sama enaka nič. Ta lastnost je poseben primer prejšnje (za k = 0).

LASTNOST 6. Če so ustrezni elementi dveh stolpcev ali dveh vrstic determinante sorazmerni, je determinanta enaka nič.

LASTNOST 7. Če je vsak element n-tega stolpca ali n-te vrstice determinante vsota dveh členov, potem lahko determinanto predstavimo kot vsoto dveh determinant, od katerih je ena v n-tem stolpcu oz. , oziroma v n -ti vrstici ima prvega iz omenjenih izrazov, drugega pa drugega; elementi na preostalih mestih so enaki za mejnike treh determinant. na primer

LASTNOST 8. Če elementom nekega stolpca (ali neke vrstice) dodamo ustrezne elemente drugega stolpca (ali druge vrstice), pomnožene s katerim koli skupnim faktorjem, se vrednost determinante ne bo spremenila. na primer

.

Nadaljnje lastnosti determinant so povezane s konceptom algebraičnega komplementa in minora. Minor nekega elementa je determinanta, pridobljena iz danega z brisanjem vrstice in stolpca, na presečišču katerega se ta element nahaja.

Algebraični komplement katerega koli elementa determinante je enak minoru tega elementa, vzetemu z lastnim predznakom, če je vsota številk vrstice in stolpca, na presečišču katerih se element nahaja, sodo število, in z nasprotnim predznakom, če je to število liho.

Algebraično dopolnilo elementa bomo označili z veliko črko istega imena in enake številke kot črka, ki označuje sam element.

LASTNOST 9. Določilno

je enak vsoti produktov elementov katerega koli stolpca (ali vrstice) z njihovimi algebrskimi komplementi.

Z drugimi besedami, veljajo naslednje enakosti:

, ,

, .

6) Minori in algebraični dodatki.

Opredelitev. Manjši element determinante je th naročilo se imenujejo determinanta- vrstni red, ki je pridobljen iz danega determinanta s prečrtanjem -te vrstice in -tega stolpca, na presečišču katerega stoji element.

Oznaka:.

Opredelitev. Algebraični dopolnitev elementa determinante reda se imenuje njegov minor, vzet s predznakom plus, če je sodo število, in z znakom minus, če je to sodo število.

Oznaka:.

Izrek. (O razširitvi determinante.)

Delominanta je enaka vsoti produktov elementov katere koli vrstice (ali katerega koli stolpca) determinante z njihovimi algebrskimi komplementi:

7) Inverzna matrika- take matrika A −1 , ko se pomnoži s katerim, izvirna matrika A Rezultati v matriko identitete E:

Kvadratna matrica je reverzibilna, če in samo če je nedegenerirana, torej njena determinanta ni nič. Za ne-kvadratne matrike in degenerirane matrice ni obratnih matrik. Vendar pa je mogoče ta koncept posplošiti in uvesti psevdoinverzne matrike, podobno kot obratno v mnogih lastnostih.

8)Matrični rang- najvišje naročilo mladoletne osebe te neničelne matrike

Običajno je rang matrike označen z () oz. Obe oznaki sta k nam prišli iz tujih jezikov, zato se lahko uporabljata obe.

Lastnosti

Izrek (o osnovnem minoru): Naj bo r = rang A M osnovni minor matrike A, potem je:

osnovne vrstice in osnovni stolpci so linearno neodvisni;

vsaka vrstica (stolpec) matrike A je linearna kombinacija osnovnih vrstic (stolpcev).

- Spusti sinico na gotovo smrt!
Naj jo boža svoboda!
Ladja pluje in reaktor ropota ...
- Pash, si zajebal?

Spomnim se, da pred 8. razredom algebre nisem maral. Sploh mi ni bilo všeč. Razjezila me je. Ker tam nisem nič razumel.

In potem se je vse spremenilo, ker sem šel skozi en kos:

V matematiki na splošno (in zlasti v algebri) je vse zgrajeno na kompetentnem in doslednem sistemu definicij. Poznaš definicije, razumeš njihovo bistvo - ostalo ne bo težko ugotoviti.

Tako je tudi s temo današnje lekcije. Podrobno bomo obravnavali več povezanih vprašanj in definicij, zahvaljujoč katerim se boste enkrat za vselej ukvarjali z matrikami, z determinantami in z vsemi njihovimi lastnostmi.

Determinante so osrednji pojem v matrični algebri. Tako kot skrajšane formule za množenje vas bodo preganjale ves čas vašega naprednega tečaja matematike. Zato dodobra beremo, gledamo in razumemo. :)

Začeli bomo z najbolj intimnim - in kaj je matrika? In kako z njim pravilno delati.

Pravilna umestitev indeksov v matriko

Matrica je le tabela, napolnjena s številkami. Neo nima nič s tem.

Ena ključnih značilnosti matrike je njena dimenzija, tj. število vrstic in stolpcev, iz katerih je sestavljen. Običajno pravijo, da ima neka matrika $ A $ velikost $ \ levo [m \ krat n \ desno] $, če ima $ m $ vrstic in $ n $ stolpcev. Pišejo takole:

ali takole:

Obstajajo še druge oznake - vse je odvisno od preferenc predavatelja / seminarista / avtorja učbenika. Toda v vsakem primeru se pri vseh teh $ \ levo [m \ krat n \ desno] $ in $ ((a) _ (ij)) $ pojavi ista težava:

Kateri indeks je za kaj odgovoren? Najprej je številka vrstice, nato stolpec? Ali obratno?

Ob branju predavanj in učbenikov se bo odgovor zdel očiten. Ko pa imaš na izpitu pred seboj le zloženko s težavo, se lahko preobremeniš in nenadoma postaneš zmeden.

Zato se lotimo tega vprašanja enkrat za vselej. Najprej se spomnimo običajnega koordinatnega sistema iz šolskega tečaja matematike:

Uvedba koordinatnega sistema na ravnini

Se je spomniš? Ima izhodiščno (točka $ O = \ levo (0; 0 \ desno) $) osi $ x $ in $ y $, vsaka točka na ravnini pa je enolično določena s koordinatami: $ A = \ levo (1; 2 \ desno) $, $ B = \ levo (3; 1 \ desno) $ itd.

Zdaj vzemimo to konstrukcijo in jo postavimo poleg matrike, tako da je izvor v zgornjem levem kotu. Zakaj tam? Ker ko odpremo knjigo, začnemo brati točno iz zgornjega levega kota strani – lažje si je zapomniti.

Kam pa naj bodo usmerjene osi? Usmerili jih bomo tako, da bodo te osi pokrile celotno našo virtualno "stran". Res je, za to morate zavrteti naš koordinatni sistem. Edina možna možnost za takšno ureditev:

Zdaj ima vsaka celica matrice enoznačne koordinate $ x $ in $ y $. Na primer, pisanje $ ((a) _ (24)) $ pomeni, da se sklicujemo na element s koordinatama $ x = 2 $ in $ y = 4 $. Dimenzije matrice so enolično nastavljene tudi s parom števil:

Samo pozorno poglejte to sliko. Poigrajte se s koordinatami (še posebej, če delate z realnimi matrikami in determinantami) - in zelo kmalu boste spoznali, da tudi v najbolj zapletenih izrekih in definicijah popolnoma razumete, kaj je na kocki.

Razumeli? No, pojdimo na prvi korak razsvetljenja - geometrijsko definicijo determinante. :)

Geometrijska definicija

Najprej bi rad omenil, da determinanta obstaja samo za kvadratne matrike oblike $ \ levo [n \ krat n \ desno] $. Determinant je število, ki se izračuna po določenih pravilih in je ena od značilnosti te matrike (obstajajo še druge značilnosti: rang, lastni vektorji, o tem pa več v drugih lekcijah).

Kakšna je torej ta lastnost? Kaj to pomeni? Preprosto je:

Determinanta kvadratne matrike $ A = \ left [n \ times n \ right] $ je prostornina $ n $ -dimenzionalnega paralelepipeda, ki nastane, če vrstice matrike upoštevamo kot vektorje, ki tvorijo robove tega paralelepiped.

Na primer, determinanta matrike 2x2 je le površina paralelograma, za matriko 3x3 pa je že prostornina 3-dimenzionalnega paralelepipeda - tistega, ki razjezi vse srednješolce pri pouku stereometrije.

Na prvi pogled se ta definicija morda zdi popolnoma neustrezna. A ne sklepajmo prehitro - poglejmo primere. Pravzaprav je vse osnovno, Watson:

Naloga. Poiščite determinante matrik:

\ [\ levo | \ začetek (matrika) 1 & 0 \\ 0 & 3 \\\ konec (matrika) \ desno | \ quad \ levo | \ begin (matrica) 1 & -1 \\ 2 & 2 \\\ end (matrika) \ desno | \ quad \ levo | \ začetek (matrika) 2 & 0 & 0 \\ 1 & 3 & 0 \\ 1 & 1 & 4 \\\ konec (matrika) \ desno | \]

Rešitev. Prvi dve kvalifikaciji sta 2x2. To so torej le področja paralelogramov. Narišimo jih in izračunajmo površino.

Prvi paralelogram je zgrajen na vektorjih $ ((v) _ (1)) = \ levo (1; 0 \ desno) $ in $ ((v) _ (2)) = \ levo (0; 3 \ desno) $:

Določevalec 2x2 je površina paralelograma

Očitno to ni le paralelogram, ampak kar pravokotnik. Njegovo območje je

Drugi paralelogram je zgrajen na vektorjih $ ((v) _ (1)) = \ levo (1; -1 \ desno) $ in $ ((v) _ (2)) = \ left (2; 2 \ desno) ) $. No, pa kaj? To je tudi pravokotnik:

Še ena determinanta 2x2

Stranice tega pravokotnika (pravzaprav dolžine vektorjev) se zlahka izračunajo s Pitagorovim izrekom:

\ [\ začni (poravnaj) & \ levo | ((v) _ (1)) \ desno | = \ sqrt (((1) ^ (2)) + ((\ levo (-1 \ desno)) ^ (2))) = \ sqrt (2); \\ & \ levo | ((v) _ (2)) \ desno | = \ sqrt (((2) ^ (2)) + ((2) ^ (2))) = \ sqrt (8) = 2 \ sqrt (2); \\ & S = \ levo | ((v) _ (1)) \ desno | \ cdot \ levo | ((v) _ (2)) \ right | = \ sqrt (2) \ cdot 2 \ sqrt (2) = 4. \\\ konec (poravnaj) \]

Ostaja še, da se ukvarjamo z zadnjo determinanto - že obstaja matrika 3x3. Spomniti se moramo stereometrije:

Določilnica 3x3 je prostornina paralelepipeda

Izgleda, da absorbira možgane, a v resnici je dovolj, da se spomnimo formule za prostornino paralelepipeda:

kjer je $ S $ območje osnove (v našem primeru je to območje paralelograma na ravnini $ OXY $), $ h $ je višina, potegnjena na to osnovo (pravzaprav je $ z $ -koordinata vektorja $ ((v) _ (3) ) $).

Območje paralelograma (narisali smo ga ločeno) je prav tako enostavno izračunati:

\ [\ začni (poravnaj) & S = 2 \ cdot 3 = 6; \\ & V = S \ cdot h = 6 \ cdot 4 = 24. \\\ konec (poravnaj) \]

To je vse! Odgovore zapišemo.

Odgovor: 3; 4; 24.

Hitra opomba o sistemu zapisov. Verjetno komu ne bo všeč, da ignoriram "puščice" nad vektorji. Domnevno lahko na ta način zamenjate vektor s točko ali čim drugim.

A bodimo resni: smo že odrasli fantje in dekleta, tako da iz konteksta odlično razumemo, kdaj gre za vektor in kdaj za točko. Puščice samo zamašijo zgodbo, že nabito z matematičnimi formulami do zrkla.

In še naprej. Načeloma nam nič ne preprečuje, da bi upoštevali determinanto matrike 1x1 - taka matrika je samo ena celica in število, zapisano v tej celici, bo determinanta. Toda tu je pomembna opomba:

V nasprotju s klasičnim volumnom nam bo determinanta dala tako imenovano » usmerjeno glasnost«, tj. prostornine, ob upoštevanju zaporedja obravnave vektorjev vrstic.

In če želite dobiti glasnost v klasičnem pomenu besede, morate vzeti determinantni modul, zdaj pa vam ni treba skrbeti za to - vseeno, v nekaj sekundah se bomo naučili šteti katero koli determinanto s kakršnimi koli predznaki , velikosti itd. :)

Algebraična definicija

Kljub vsej lepoti in jasnosti geometrijskega pristopa ima resno pomanjkljivost: nič nam ne pove o tem, kako izračunati prav to determinanto.

Zato bomo zdaj analizirali alternativno definicijo - algebraično. Za to potrebujemo kratko teoretično pripravo, na koncu pa bomo dobili orodje, ki nam omogoča, da v matrikah štejemo karkoli in kakor želimo.

Res je, pojavila se bo nova težava ... ampak najprej najprej.

Permutacije in inverzije

Zapišemo številke od 1 do $ n $ v vrstico. Na koncu dobiš nekaj takega:

Zdaj (čisto za zabavo) zamenjajmo nekaj številk. Sosednje lahko spremenite:

Ali pa lahko - ne zelo sosednje:

Veš kaj? Ampak nič! V algebri se to sranje imenuje permutacija. In ima kup lastnine.

Opredelitev. Permutacija dolžine $ n $ je niz $ n $ različnih števil, zapisanih v poljubnem zaporedju. Običajno se upoštevajo prva $ n $ naravna števila (to je samo števila 1, 2, ..., $ n $), nato pa se mešajo, da dobimo želeno permutacijo.

Permutacije so označene na enak način kot vektorji - samo črka in zaporedni seznam njihovih elementov v oklepajih. Na primer: $ p = \ levo (1; 3; 2 \ desno) $ ali $ p = \ levo (2; 5; 1; 4; 3 \ desno) $. Pismo je lahko karkoli, vendar naj bo $ p $. :)

Nadalje, zaradi preprostosti bomo delali s permutacijami dolžine 5 - že so dovolj resne, da opazijo kakršne koli sumljive učinke, vendar še niso tako hude za nezrele možgane kot permutacije dolžine 6 ali več. Tu so primeri takšnih permutacij:

\ [\ začni (poravnaj) & ((p) _ (1)) = \ levo (1; 2; 3; 4; 5 \ desno) \\ & ((p) _ (2)) = \ levo (1 ; 3; 2; 5; 4 \ desno) \\ & ((p) _ (3)) = \ levo (5; 4; 3; 2; 1 \ desno) \\\ konec (poravnaj) \]

Seveda lahko permutacijo dolžine $ n $ gledamo kot funkcijo, ki je definirana na množici $ \ left \ (1; 2; ...; n \ right \) $ in bijektivno preslika to množico na sebe. Če se vrnemo k pravkar zapisanim permutacijam $ ((p) _ (1)) $, $ ((p) _ (2)) $ in $ ((p) _ (3)) $, lahko povsem zakonito zapišemo:

\ [((p) _ (1)) \ levo (1 \ desno) = 1; ((p) _ (2)) \ levo (3 \ desno) = 2; ((p) _ (3)) \ levo (2 \ desno) = 4; \]

Število različnih permutacij dolžine $ n $ je vedno omejeno in enako $ n! $ - to je lahko dokazljivo dejstvo iz kombinatorike. Na primer, če želimo zapisati vse permutacije dolžine 5, bomo oklevali, saj bodo takšne permutacije

Ena ključnih značilnosti vsake permutacije je število inverzij v njej.

Opredelitev. Inverzija v permutaciji $ p = \ levo (((a) _ (1)); ((a) _ (2)); ...; ((a) _ (n)) \ desno) $ - kateri koli par $ \ levo (((a) _ (i)); ((a) _ (j)) \ desno) $ tako, da $ i \ lt j $, vendar $ ((a) _ (i)) \ gt ( ( a) _ (j)) $. Preprosto povedano, inverzija je, ko je večje število levo od manjšega (ne nujno sosednjega).

Z $ N \ levo (p \ desno) $ bomo označili število inverzij v permutaciji $ p $, vendar bodite pripravljeni na srečanje z drugimi oznakami v različnih učbenikih in različnih avtorjih - tukaj ni enotnih standardov. Tema inverzij je zelo obsežna in temu bo posvečena ločena lekcija. Zdaj je naša naloga preprosto, da se naučimo, kako jih prešteti v resničnih težavah.

Na primer, preštejmo število inverzij v permutaciji $ p = \ levo (1; 4; 5; 3; 2 \ desno) $:

\ [\ levo (4; 3 \ desno); \ levo (4; 2 \ desno); \ levo (5; 3 \ desno); \ levo (5; 2 \ desno); \ levo (3; 2 \ desno) ). \]

Torej $ N \ levo (p \ desno) = 5 $. Kot vidite, s tem ni nič narobe. Naj vam takoj povem: nadalje nas bo zanimalo ne toliko samo število $ N \ levo (p \ desno) $, kot njegova sodnost / nenavadnost. In tukaj gladko preidemo na ključni izraz današnje lekcije.

Kaj je determinanta

Naj bo podana kvadratna matrika $ A = \ levo [n \ krat n \ desno] $. Nato:

Opredelitev. Delominanta matrike $ A = \ levo [n \ krat n \ desno] $ je algebraična vsota $ n!$ Izrazov, sestavljenih na naslednji način. Vsak člen je produkt $ n $ matričnih elementov, vzetih po en iz vsake vrstice in vsakega stolpca, pomnoženih z (−1) na moč števila inverzij:

\ [\ levo | A \ desno | = \ vsota \ meje_ (n{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}

Temeljna točka pri izbiri faktorjev za vsak izraz v determinanti je dejstvo, da ni dveh faktorjev v isti vrstici ali v istem stolpcu.

Zaradi tega lahko brez izgube splošnosti domnevamo, da indeksi $ i $ faktorjev $ ((a) _ (i; j)) $ "tečejo skozi" vrednosti 1, ..., $ n $ , in indeksi $ j $ so nekatera permutacija prvega:

In ko pride do permutacije $ p $, lahko enostavno izračunamo inverzije $ N \ left (p \ right) $ - in naslednji člen determinante je pripravljen.

Seveda nihče ne prepoveduje zamenjave množiteljev v katerem koli terminu (ali v vseh naenkrat - zakaj bi izgubljali čas za malenkosti?), In potem bodo prvi indeksi predstavljali tudi neko permutacijo. Toda na koncu se ne bo nič spremenilo: skupno število inverzij v indeksih $ i $ in $ j $ ohranja pariteto pod takšnimi perverzijami, kar je povsem skladno s starim dobrim pravilom:

Prerazporeditev faktorjev ne spremeni produkta številk.

Samo ne vežite tega pravila z množenjem matrik - za razliko od množenja števil, ni komutativno. Ampak se oddaljim. :)

Matrica 2x2

Pravzaprav lahko upoštevate matriko 1x1 - to bo ena celica, njena determinanta pa je, kot morda uganete, enaka številu, zapisani v tej celici. Nič zanimivega.

Razmislimo torej o kvadratni matriki 2x2:

\ [\ levo [\ začetek (matrika) ((a) _ (11)) & ((a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ konec (matrika) \ desno] \]

Ker je število vrstic v njej $ n = 2 $, bo determinanta vsebovala $ n! = 2! = 1 \ cdot 2 = 2 $ členov. Izpišimo jih:

\ [\ begin (align) & ((\ left (-1 \ right)) ^ (N \ left (1; 2 \ right))) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((\ levo (-1 \ desno)) ^ (0)) \ cdot ((a) _ (11)) \ cdot ((a) _ (22)) = ((a) _ (11)) ((a) _ (22)); \\ & ((\ levo (-1 \ desno)) ^ (N \ levo (2; 1 \ desno))) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((\ levo (-1 \ desno)) ^ (1)) \ cdot ((a) _ (12)) \ cdot ((a) _ (21)) = ((a) _ (12)) ( (a) _ (21)). \\\ konec (poravnaj) \]

Očitno v permutaciji $ \ left (1; 2 \ right) $, ki je sestavljena iz dveh elementov, ni inverzij, zato je $ N \ left (1; 2 \ right) = 0 $. Toda v permutaciji $ \ levo (2; 1 \ desno) $ obstaja ena inverzija (pravzaprav 2< 1), поэтому $N\left(2;1 \right)=1.$

Skupno je univerzalna formula za izračun determinante za matriko 2x2 videti takole:

\ [\ levo | \ začetek (matrika) ((a) _ (11)) & ((a) _ (12)) \\ ((a) _ (21)) & ((a) _ (22)) \\\ konec ( matrika) \ desno | = ((a) _ (11)) ((a) _ (22)) - ((a) _ (12)) ((a) _ (21)) \]

Grafično lahko to predstavimo kot produkt elementov na glavni diagonali, minus produkt elementov na stranski:

Poglejmo si nekaj primerov:

\ [\ levo | \ začetek (matrika) 5 & 6 \\ 8 & 9 \\\ konec (matrika) \ desno |; \ quad \ levo | \ začetek (matrika) 7 & 12 \\ 14 & 1 \\\ konec (matrika) \ desno |. \]

Rešitev. Vse se šteje v eno vrstico. Prva matrica:

In drugi:

Odgovor: −3; −161.

Vendar je bilo preveč enostavno. Poglejmo matrice 3x3 – tam je že zanimivo.

3x3 matrica

Zdaj razmislite o kvadratni matriki 3x3:

\ [\ levo [\ začetek (matrika) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\ ((a) _ (31)) & ((a) _ (32)) & ((a) _ (33) ) \\\ konec (matrika) \ desno] \]

Pri izračunu njegove determinante dobimo $3! = 1 \ cdot 2 \ cdot 3 = 6 $ izrazov - ne preveč za paniko, vendar dovolj, da začnemo iskati nekaj vzorcev. Najprej napišemo vse permutacije treh elementov in izračunajmo inverzije v vsakem od njih:

\ [\ začni (poravnaj) & ((p) _ (1)) = \ levo (1; 2; 3 \ desno) \ Desno N \ levo (((p) _ (1)) \ desno) = N \ levo (1; 2; 3 \ desno) = 0; \\ & ((p) _ (2)) = \ levo (1; 3; 2 \ desno) \ Desno N \ levo (((p) _ (2)) \ desno) = N \ levo (1; 3 ; 2 \ desno) = 1; \\ & ((p) _ (3)) = \ levo (2; 1; 3 \ desno) \ Desno N \ levo (((p) _ (3)) \ desno) = N \ levo (2; 1 ; 3 \ desno) = 1; \\ & ((p) _ (4)) = \ levo (2; 3; 1 \ desno) \ Desno N \ levo (((p) _ (4)) \ desno) = N \ levo (2; 3 ; 1 \ desno) = 2; \\ & ((p) _ (5)) = \ levo (3; 1; 2 \ desno) \ Desno N \ levo (((p) _ (5)) \ desno) = N \ levo (3; 1 ; 2 \ desno) = 2; \\ & ((p) _ (6)) = \ levo (3; 2; 1 \ desno) \ Desno N \ levo (((p) _ (6)) \ desno) = N \ levo (3; 2 ; 1 \ desno) = 3. \\\ konec (poravnaj) \]

Kot je bilo pričakovano, se bo spremenilo skupno 6 permutacij $ ((p) _ (1)) $, ... $ ((p) _ (6)) $), število inverzij v njih pa se spremeni od 0 do 3.

Na splošno bomo imeli tri izraze z "plus" (kjer je $ N \ levo (p \ desno) $ sodo) in še tri z "minus". Na splošno se determinanta izračuna po formuli:

\ [\ levo | \ begin (matrica) ((a) _ (11)) & ((a) _ (12)) & ((a) _ (13)) \\ ((a) _ (21)) & ((a) _ (22)) & ((a) _ (23)) \\ ((a) _ (31)) & ((a) _ (32)) & ((a) _ (33)) \\\ konec (matrika) \ desno | = \ začetek (matrika) ((a) _ (11)) ((a) _ (22)) ((a) _ (33)) + ((a) _ (12)) ( (a) _ (23)) ((a) _ (31)) + ((a) _ (13)) ((a) _ (21)) ((a) _ (32)) - \\ - ( (a) _ (13)) ((a) _ (22)) ((a) _ (31)) - ((a) _ (12)) ((a) _ (21)) ((a) _ (33)) - ((a) _ (11)) ((a) _ (23)) ((a) _ (32)) \\\ konec (matrika) \]

Samo ne sedite in zdaj hudo nabijajte vse te indekse! Namesto nerazumljivih številk si je bolje zapomniti naslednje mnemonično pravilo:

Pravilo trikotnika. Če želite poiskati determinanto matrike 3x3, morate dodati tri produkte elementov na glavni diagonali in na ogliščih enakokrakih trikotnikov s stranico, vzporedno s to diagonalo, in nato odšteti iste tri produkte, vendar na stranski diagonali. Shematično izgleda takole:

3x3 matrična determinanta: pravilo trikotnika

Prav te trikotnike (ali pentagrame - kot želite) radi rišejo v vse vrste učbenikov in priročnikov o algebri. Vendar ne govorimo o žalostnih stvareh. Raje izračunajmo eno takšno determinanto - za ogrevanje pred pravo pločevino. :)

Naloga. Izračunaj determinanto:

\ [\ levo | \ začetek (matrika) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 1 \\\ konec (matrika) \ desno | \]

Rešitev. Delamo po pravilu trikotnikov. Najprej štejemo tri izraze, sestavljene iz elementov na glavni diagonali in vzporednih z njo:

\ [\ začetek (poravnaj) & 1 \ cdot 5 \ cdot 1 + 2 \ cdot 6 \ cdot 7 + 3 \ cdot 4 \ cdot 8 = \\ & = 5 + 84 + 96 = 185 \\\ konec (poravnaj) \]

Zdaj se ukvarjamo s stransko diagonalo:

\ [\ start (poravnaj) & 3 \ cdot 5 \ cdot 7 + 2 \ cdot 4 \ cdot 1 + 1 \ cdot 6 \ cdot 8 = \\ & = 105 + 8 + 48 = 161 \\\ konec (poravnaj) \]

Ostaja le, da od prve številke odštejemo drugo - in dobili bomo odgovor:

To je vse!

Vendar matrične determinante 3x3 še niso vrhunec spretnosti. Naslednje nas čaka najbolj zanimivo. :)

Splošna shema za izračun determinant

Kot vemo, ko dimenzija matrike $ n $ raste, je število členov v determinanti $ n! $ in hitro raste. Navsezadnje faktorial za vas ni prekleta stvar, precej hitro rastoča funkcija.

Že za matrike 4x4 postane nekako premalo dobro upoštevati determinante neposredno naprej (t.j. skozi permutacije). Približno 5x5 in bolj na splošno molči. Zato so nekatere lastnosti determinante povezane s primerom, vendar je za njihovo razumevanje potrebno malo teoretičnega usposabljanja.

pripravljeni? Pojdi!

Kaj je Matrix Minor

Naj bo podana poljubna matrika $ A = \ levo [m \ krat n \ desno] $. Opomba: Ni nujno, da je kvadratna. Za razliko od determinant so mladoletniki take stvari, ki obstajajo ne le v ostrih kvadratnih matrikah. Izberimo več (na primer $ k $) vrstic in stolpcev v tej matriki z $ 1 \ le k \ le m $ in $ 1 \ le k \ le n $. Nato:

Opredelitev. Minor reda $ k $ je determinanta kvadratne matrike, ki nastane na presečišču izbranih $ k $ stolpcev in vrstic. To novo matriko bomo imenovali tudi minor.

Tak minor je označen kot $ ((M) _ (k)) $. Seveda ima lahko ena matrika cel kup minorov reda $ k $. Tukaj je primer manjšega reda 2 za matriko $ \ levo [5 \ krat 6 \ desno] $:

Izbira $ k = 2 $ stolpcev in vrstic za oblikovanje manjše vrednosti

Izbrane vrstice in stolpci niso potrebni drug ob drugem, kot v zgornjem primeru. Glavna stvar je, da je število izbranih vrstic in stolpcev enako (to je število $ k $).

Obstaja tudi druga definicija. Mogoče bo komu bolj všeč:

Opredelitev. Naj bo podana pravokotna matrika $ A = \ levo [m \ krat n \ desno] $. Če po brisanju enega ali več stolpcev in ene ali več vrstic v njem nastane kvadratna matrika velikosti $ \ levo [k \ krat k \ desno] $, potem je njen determinant manjši $ ((M) _ (k) ) $ ... Tudi sami matriki bomo včasih rekli minor - to bo jasno iz konteksta.

Kot je rekel moj maček, je včasih bolje, da se zbudiš iz 11. nadstropja, da enkrat pojedo hrano, kot pa mijavkat, ko sediš na balkonu.

Primer. Podano matriko

Z izbiro vrstice 1 in stolpca 2 dobimo minor prvega reda:

\ [((M) _ (1)) = \ levo | 7 \ desno | = 7 \]

Če izberemo vrstice 2, 3 in stolpce 3, 4, dobimo minor drugega reda:

\ [((M) _ (2)) = \ levo | \ začetek (matrika) 5 & 3 \\ 6 & 1 \\\ konec (matrika) \ desno | = 5-18 = -13 \]

In če izberete vse tri vrstice, pa tudi stolpce 1, 2, 4, bo prišlo do manjšega tretjega reda:

\ [((M) _ (3)) = \ levo | \ začetek (matrika) 1 & 7 & 0 \\ 2 & 4 & 3 \\ 3 & 0 & 1 \\\ konec (matrika) \ desno | \]

Bralcu ne bo težko najti še drugih mladoletnikov naročil 1, 2 ali 3. Zato pojdimo naprej.

Algebraična dopolnila

"No ok, in kaj nam dajejo ti sluge?" - verjetno vprašaš. Sami, nič. Toda v kvadratnih matrikah ima vsak minor "spremljevalca" - dodatni minor, pa tudi algebraično dopolnilo. Ta dva trika nam bosta skupaj omogočila, da kliknemo na kvalifikacije kot orehi.

Opredelitev. Naj bo podana kvadratna matrika $ A = \ left [n \ times n \ right] $, v kateri je izbran manjši $ ((M) _ (k)) $. Potem je dodatni minor za minor $ ((M) _ (k)) $ del prvotne matrike $ A $, ki ostane po brisanju vseh vrstic in stolpcev, ki sodelujejo pri sestavljanju manjšega $ ((M) _ ( k)) $:

Dodatni minor k manjši $ ((M) _ (2)) $

Pojasnimo eno točko: dodatni mol ni le "kos matrice", temveč determinanta tega dela.

Dodatni mladoletniki so označeni z zvezdico: $ M_ (k) ^ (*) $:

kjer operacija $ A \ nabla ((M) _ (k)) $ dobesedno pomeni "izbriši iz $ A $ vrstice in stolpce, vključene v $ ((M) _ (k)) $". Ta operacija v matematiki ni splošno sprejeta - pravkar sem si jo sam izmislil zaradi lepote zgodbe. :)

Komplementarni mladoletniki se redko uporabljajo samostojno. So del bolj zapletene konstrukcije, algebrskega dopolnila.

Opredelitev. Minorni dodatek $ ((M) _ (k)) $ je dodatni minor $ M_ (k) ^ (*) $, pomnožen z $ ((\ levo (-1 \ desno)) ^ (S)) $ , kjer je $ S $ je vsota številk vseh vrstic in stolpcev, vključenih v prvotni minor $ ((M) _ (k)) $.

Praviloma je algebraično pomožno dopolnilo $ ((M) _ (k)) $ označeno z $ ((A) _ (k)) $. Zato:

\ [((A) _ (k)) = ((\ levo (-1 \ desno)) ^ (S)) \ cdot M_ (k) ^ (*) \]

Težko? Na prvi pogled ja. Ampak ni ravno. Ker v resnici je vse enostavno. Poglejmo primer:

Primer. Glede na matriko 4x4:

Izberimo maloletnika drugega reda

\ [((M) _ (2)) = \ levo | \ začetek (matrika) 3 & 4 \\ 15 in 16 \\\ konec (matrika) \ desno | \]

Captain Obvious nam nekako namiguje, da sta pri sestavljanju tega minora sodelovali vrstici 1 in 4 ter stolpca 3 in 4. Prečrtaj jih - dobimo dodatni mol:

Ostaja še najti število $ S $ in pridobiti algebraično dopolnilo. Ker poznamo številke vključenih vrstic (1 in 4) in stolpcev (3 in 4), je vse preprosto:

\ [\ začni (poravnaj) & S = 1 + 4 + 3 + 4 = 12; \\ & ((A) _ (2)) = ((\ levo (-1 \ desno)) ^ (S)) \ cdot M_ (2) ^ (*) = ((\ levo (-1 \ desno) ) ^ (12)) \ cdot \ levo (-4 \ desno) = - 4 \ konec (poravnaj) \]

Odgovor: $ ((A) _ (2)) = - 4 $

To je vse! Pravzaprav je vsa razlika med dodatnim manjšim in algebrskim dopolnjevanjem le v minusu spredaj in tudi takrat ne vedno.

Laplaceov izrek

In tako smo prišli do tega, zakaj so bili pravzaprav potrebni vsi ti minori in algebraični dodatki.

Laplaceov izrek o razširitvi determinante. Naj bo $ k $ vrstic (stolpcev) izbranih v matriki velikosti $ \ levo [n \ krat n \ desno] $, z $ 1 \ le k \ le n-1 $. Potem je determinanta te matrike enaka vsoti vseh produktov minorov reda $ k $, ki jih vsebujejo izbrane vrstice (stolpci) z njihovimi algebrskimi komplementi:

\ [\ levo | A \ desno | = \ vsota (((M) _ (k)) \ cdot ((A) _ (k))) \]

Poleg tega bo natanko $ C_ (n) ^ (k) $ takih izrazov.

V redu, v redu: približno $ C_ (n) ^ (k) $ - o tem že govorim, v prvotnem Laplaceovem izreku ni bilo nič takega. Toda kombinatorike ni nihče preklical in dobesedno bežen pogled na pogoj vam bo omogočil, da se sami prepričate, da bo izrazov točno toliko. :)

Tega ne bomo dokazovali, čeprav to ne predstavlja nobene posebne težave - vsi izračuni so reducirani na dobre stare permutacije in sode / lihe inverzije. Kljub temu bo dokaz predstavljen v ločenem odstavku, danes pa imamo čisto praktično lekcijo.

Zato preidemo na poseben primer tega izreka, ko so minori ločene celice matrike.

Dekompozicija determinant po vrstici in stolpcu

Zdaj bo govora ravno o glavnem orodju za delo z determinantami, zaradi katerega se je začela vsa ta igra s permutacijami, minorji in algebrskimi dodatki.

Preberite in uživajte:

Posledica Laplaceovega izreka (razširitev determinante v vrstico/stolpec). Naj bo izbrana ena vrstica v matriki velikosti $ \ levo [n \ krat n \ desno] $. Mladoletniki v tej vrstici bodo $ n $ posameznih celic:

\ [((M) _ (1)) = ((a) _ (ij)), \ quad j = 1, ..., n \]

Dodatne manjše vrednosti je prav tako enostavno izračunati: samo vzemite izvirno matriko in izbrišite vrstico in stolpec, ki vsebujeta $ ((a) _ (ij)) $. Takim mladoletnikom poimenujmo $ M_ (ij) ^ (*) $.

Za algebraično dopolnilo je še vedno potrebno število $ S $, toda v primeru minora reda 1 je to le vsota "koordinat" celice $ ((a) _ (ij)) $:

Nato lahko izvirno determinanto zapišemo v smislu $ ((a) _ (ij)) $ in $ M_ (ij) ^ (*) $ v skladu z Laplaceovim izrekom:

\ [\ levo | A \ desno | = \ vsota \ omejitve_ (j = 1) ^ (n) (((a) _ (ij)) \ cdot ((\ levo (-1 \ desno)) ^ (i + j)) \ cdot ((M) _ (ij))) \]

To je tisto, kar je formula za razširitev niza... Toda enako velja za stolpce.

Iz tega sledi je mogoče potegniti več sklepov:

1. Ta shema deluje enako dobro za vrstice in stolpce. Pravzaprav bo pogosteje razširitev potekala v stolpcu in ne v vrstici.
2. Število izrazov v razširitvi je vedno točno $ n $. To je bistveno manj kot $ C_ (n) ^ (k) $ in še bolj $ n! $.
3. Namesto ene determinante $ \ levo [n \ krat n \ desno] $, boste morali prešteti več determinant velikosti ena manj: $ \ left [\ left (n-1 \ right) \ times \ left (n-1 \ desno) \ desno ] $.

Slednje dejstvo je še posebej pomembno. Na primer, namesto brutalne determinante 4x4 bo zdaj dovolj, da preštejemo več determinant 3x3 - nekako se bomo z njimi spopadli. :)

Naloga. Poiščite determinanto:

\ [\ levo | \ začetek (matrika) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\ konec (matrika) \ desno | \]

Rešitev. Razširimo to determinanto vzdolž prve vrstice:

\ [\ začni (poravnaj) \ levo | A \ desno | = 1 \ cdot ((\ levo (-1 \ desno)) ^ (1 + 1)) \ cdot \ levo | \ začetek (matrika) 5 & 6 \\ 8 & 9 \\\ konec (matrika) \ desno | + & \\ 2 \ cdot ((\ levo (-1 \ desno)) ^ (1 + 2)) \ cdot \ levo | \ začetek (matrika) 4 & 6 \\ 7 & 9 \\\ konec (matrika) \ desno | + & \\ 3 \ cdot ((\ levo (-1 \ desno)) ^ (1 + 3)) \ cdot \ levo | \ začetek (matrika) 4 & 5 \\ 7 in 8 \\\ konec (matrika) \ desno | = & \\\ konec (poravnava) \]

\ [\ start (align) & = 1 \ cdot \ left (45-48 \ right) -2 \ cdot \ left (36-42 \ right) +3 \ cdot \ left (32-35 \ right) = \\ & = 1 \ cdot \ levo (-3 \ desno) -2 \ cdot \ levo (-6 \ desno) +3 \ cdot \ levo (-3 \ desno) = 0. \\\ konec (poravnaj) \]

Naloga. Poiščite determinanto:

\ [\ levo | \ začetek (matrika) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ konec (matrika) \ desno | \ ]

Rešitev. Za spremembo tokrat delajmo s stolpci. Na primer, zadnji stolpec vsebuje dve ničli naenkrat - očitno bo to znatno zmanjšalo izračune. Zdaj boste videli zakaj.

Torej razširimo determinanto za četrti stolpec:

\ [\ start (align) \ left | \ začetek (matrika) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ konec (matrika) \ desno | = 0 \ cdot ((\ levo (-1 \ desno)) ^ (1 + 4)) \ cdot \ levo | \ začetek (matrika) 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ konec (matrika) \ desno | + & \\ +1 \ cdot ((\ levo (-1 \ desno)) ^ (2 + 4)) \ cdot \ levo | \ začetek (matrika) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ konec (matrika) \ desno | + & \\ +1 \ cdot ((\ levo (-1 \ desno)) ^ (3 + 4)) \ cdot \ levo | \ začetek (matrika) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ konec (matrika) \ desno | + & \\ +0 \ cdot ((\ levo (-1 \ desno)) ^ (4 + 4)) \ cdot \ levo | \ začetek (matrika) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\ konec (matrika) \ desno | & \\\ konec (poravnaj) \]

In potem - o, čudež! - dva izraza takoj odideta, saj imata množitelj "0". Še vedno obstajata dve determinanti 3x3, s katerimi se zlahka spopademo:

\ [\ začni (poravnaj) & \ levo | \ begin (matrika) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\ end (matrika) \ desno | = 0 + 0 + 1-1-1-0 = -1; \\ & \ levo | \ začetek (matrika) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\ konec (matrika) \ desno | = 0 + 1 + 1-0-0-1 = 1. \\\ konec (poravnaj) \]

Vrnemo se k viru in najdemo odgovor:

\ [\ levo | \ začetek (matrika) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\ konec (matrika) \ desno | = 1 \ cdot \ levo (-1 \ desno) + \ levo (-1 \ desno) \ cdot 1 = -2 \]

Torej to je vse. In ne 4! = 24 izrazov ni bilo treba šteti. :)

Odgovor: −2

Osnovne lastnosti determinante

V zadnjem problemu smo videli, kako prisotnost nič v vrsticah (stolpcih) matrike močno poenostavi razširitev determinante in na splošno vse izračune. Postavlja se naravno vprašanje: ali je mogoče, da se te ničle pojavijo tudi v matriki, kjer prvotno niso bile?

Odgovor je nedvoumen: lahko... In tukaj nam na pomoč priskočijo lastnosti determinante:

1. Če zamenjate dve vrstici (stolpca) na mestih, se determinanta ne bo spremenila;
2. Če eno vrstico (stolpec) pomnožimo s številom $ k $, se celotna determinanta pomnoži tudi s številom $ k $;
3. Če vzamete eno vrstico in jo dodate (odštejete) od druge tolikokrat, kot želite, se determinanta ne bo spremenila;
4. Če sta dve vrstici determinante enaki, bodisi sorazmerni, ali je ena od vrstic napolnjena z ničlami, potem je celotna determinanta nič;
5. Vse zgornje lastnosti veljajo tudi za stolpce.
6. Ko je matrika transponirana, se determinanta ne spremeni;
7. Delominanta matričnega produkta je enaka zmnožku determinant.

Tretja lastnost je še posebej dragocena: zmoremo odštejte drugo od ene vrstice (stolpca), dokler se na pravih mestih ne pojavijo ničle.

Najpogosteje se izračuni skrčijo na to, da se celoten stolpec "ničli" povsod, razen enega elementa, in nato razširi determinanto vzdolž tega stolpca, pri čemer dobimo matriko 1 manjše velikosti.

Poglejmo, kako to deluje v praksi:

Naloga. Poiščite determinanto:

\ [\ levo | \ začetek (matrika) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ konec (matrika) \ desno | \ ]

Rešitev. Tu sploh ni nič, zato lahko "udarite" v katero koli vrstico ali stolpec - količina izračunov bo približno enaka. Ne izgubljajmo časa za malenkosti in »ničlimo« prvi stolpec: že ima celico z eno, zato samo vzemite prvo vrstico in jo 4-krat odštejte od druge, 3-krat od tretjega in 2-krat od zadnje.

Kot rezultat bomo dobili novo matriko, vendar bo njen determinant enak:

\ [\ začetek (matrika) \ levo | \ začetek (matrika) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\\ konec (matrika) \ desno | \ začetek (matrika) \ puščica navzdol \\ -4 \\ -3 \\ -2 \\\ konec (matrika) = \\ = \ levo | \ begin (matrika) 1 & 2 & 3 & 4 \\ 4-4 \ cdot 1 & 1-4 \ cdot 2 & 2-4 \ cdot 3 & 3-4 \ cdot 4 \\ 3-3 \ cdot 1 & 4-3 \ cdot 2 & 1-3 \ cdot 3 & 2-3 \ cdot 4 \\ 2-2 \ cdot 1 & 3-2 \ cdot 2 & 4-2 \ cdot 3 & 1-2 \ cdot 4 \ \\ konec (matrika) \ desno | = \\ = \ levo | \ začetek (matrika) 1 & 2 & 3 & 4 \\ 0 & -7 & -10 & -13 \\ 0 & -2 & -8 & -10 \\ 0 & -1 & -2 & -7 \\ \ konec (matrika) \ desno | \\\ konec (matrika) \]

Zdaj, s Pujskovo mirnostjo, razširimo to determinanto glede na prvi stolpec:

\ [\ začetek (matrika) 1 \ cdot ((\ levo (-1 \ desno)) ^ (1 + 1)) \ cdot \ levo | \ začetek (matrika) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ konec (matrika) \ desno | +0 \ cdot ((\ levo (-1 \ desno)) ^ (2 + 1)) \ cdot \ levo | ... \ desno | + \\ +0 \ cdot ((\ levo (-1 \ desno)) ^ (3 + 1)) \ cdot \ levo | ... \ desno | +0 \ cdot ((\ levo (-1 \ desno)) ^ (4 + 1)) \ cdot \ levo | ... \ desno | \\\ konec (matrika) \]

Jasno je, da bo "preživel" le prvi izraz - v preostalem nisem niti zapisal determinant, saj se tako ali tako pomnožijo z nič. Koeficient pred determinanto je enak ena, t.j. ni ti treba zapisati.

Lahko pa vzamete "minuse" iz vseh treh vrstic determinante. Pravzaprav smo faktor (−1) premaknili trikrat:

\ [\ levo | \ začetek (matrika) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\ konec (matrika) \ desno | = \ cdot \ levo | \ začetek (matrika) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ konec (matrika) \ desno | \]

Dobili smo majhno determinanto 3x3, ki jo lahko že izračunamo po pravilu trikotnikov. Vendar ga bomo poskušali razstaviti glede na prvi stolpec - na srečo zadnja vrstica ponosno vsebuje enega:

\ [\ begin (align) & \ left (-1 \ right) \ cdot \ left | \ začetek (matrika) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\\ konec (matrika) \ desno | \ začetek (matrika) -7 \\ -2 \\ \ uparrow \ \\ konec (matrika) = \ levo (-1 \ desno) \ cdot \ levo | \ začetek (matrika) 0 & -4 & -36 \\ 0 & 4 & -4 \\ 1 & 2 & 7 \\\ konec (matrika) \ desno | = \\ & = \ cdot \ levo | \ begin (matrica) -4 & -36 \\ 4 & -4 \\\ end (matrica) \ right | = \ left (-1 \ right) \ cdot \ left | \ začetek (matrika) -4 & -36 \\ 4 & -4 \\\ konec (matrika) \ desno | \\\ konec (poravnaj) \]

Seveda se lahko še vedno zabavate in razširite matriko 2x2 po vrsticah (stolpcih), vendar smo mi ustrezni, zato bomo samo izračunali odgovor:

\ [\ levo (-1 \ desno) \ cdot \ levo | \ začetek (matrika) -4 & -36 \\ 4 & -4 \\\ konec (matrika) \ desno | = \ levo (-1 \ desno) \ cdot \ levo (16 + 144 \ desno) = - 160 \ ]

Tako se razblinijo sanje. Samo −160 v odgovoru. :)

Odgovor: -160.

Nekaj ​​opomb, preden preidemo na zadnjo nalogo:

1. Prvotna matrica je bila simetrična glede stranske diagonale. Vsi minori v razširitvi so tudi simetrični glede na isto stransko diagonalo.
2. Strogo gledano, nismo mogli nič razširiti, ampak preprosto spraviti matriko v zgornjo trikotno obliko, ko so pod glavno diagonalo trdne ničle. Potem je (mimogrede natančno v skladu z geometrijsko interpretacijo) determinanta enaka zmnožku $ ((a) _ (ii)) $ - številk na glavni diagonali.

Naloga. Poiščite determinanto:

\ [\ levo | \ begin (matrika) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ end (matrika) \ desno | \ ]

Rešitev. No, tukaj prva vrstica prosi za "ničlo". Vzamemo prvi stolpec in od vseh ostalih odštejemo natanko enkrat:

\ [\ začni (poravnaj) & \ levo | \ begin (matrika) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\\ end (matrika) \ desno | = \\ & = \ levo | \ začni (matrika) 1 & 1-1 & 1-1 & 1-1 \\ 2 & 4-2 & 8-2 & 16-2 \\ 3 & 9-3 & 27-3 & 81-3 \\ 5 & ​​25-5 & 125-5 & 625-5 \\\ konec (matrika) \ desno | = \\ & = \ levo | \ začetek (matrika) 1 & 0 & 0 & 0 \\ 2 & 2 & 6 & 14 \\ 3 & 6 & 24 & 78 \\ 5 & 20 & 120 & 620 \\\ konec (matrika) \ desno | \\\ konec (poravnaj) \]

V prvi vrstici razširimo, nato pa iz preostalih vrstic vzamemo skupne faktorje:

\ [\ cdot \ levo | \ začetek (matrika) 2 & 6 & 14 \\ 6 & 24 & 78 \\ 20 & 120 & 620 \\\ konec (matrika) \ desno | = \ cdot \ levo | \ begin (matrika) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ end (matrika) \ desno | \]

Spet opazimo "lepe" številke, a že v prvem stolpcu - determinanto razširimo glede na to:

\ [\ začetek (poravnaj) & 240 \ cdot \ levo | \ začetek (matrika) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\\ konec (matrika) \ desno | \ začetek (matrika) \ puščica navzdol \\ -1 \\ -1 \ \\ konec (matrika) = 240 \ cdot \ levo | \ začetek (matrika) 1 & 3 & 7 \\ 0 & 1 & 6 \\ 0 & 3 & 24 \\\ konec (matrika) \ desno | = \\ & = 240 \ cdot ((\ levo (-1 \ desno)) ^ (1 + 1)) \ cdot \ levo | \ začetek (matrika) 1 & 6 \\ 3 & 24 \\\ konec (matrika) \ desno | = \\ & = 240 \ cdot 1 \ cdot \ levo (24-18 \ desno) = 1440 \\\ konec ( poravnaj) \]

Naročite. Problem je rešen.

Odgovor: 1440

1. Splošno pravilo znakov. V nadaljevanju bo koristno ugotoviti, s kakšnim predznakom je izraz vključen v determinanto, kjer sta dve permutaciji števil.

Če želite to ugotoviti, morate faktorje razporediti po vrstnem redu vrstic. Upoštevajte, da če zamenjamo dva faktorja, pride do transpozicije tako v prvem kot v drugem indeksu, tako da se število inverzij v prvih indeksih in število inverzij v drugih indeksih spremeni v liho število, zato se spremeni njihova vsota. na sodo število. Zato se ne spremeni s spremembo mest dveh faktorjev in torej s kakršno koli spremembo vrstnega reda faktorjev, ker je vsaka sprememba vrstnega reda enakovredna več parnim spremembam krajev. Iz tega sledi, da je znak, s katerim izraz vstopi v determinanto. Dejansko naj je zaporedje številk stolpcev, potem ko faktorje privedemo v vrstni red vrstic, tako da Potem

in to je faktor ± 1, s katerim je v determinanto vključen izraz, ki nas zanima.

2. Determinanta transponirane matrike je enaka izvirni. Z drugimi besedami, determinanta se ne spremeni, ko je matrika transponirana.

Dejansko je vzeti produkte elementov enega iz vsake vrstice in enega iz vsakega stolpca prvotne matrike enako kot to storiti glede na transponirano matriko. Nadalje so številke vrstic za izvirnik številke stolpcev za prestavljeni, številke stolpcev za izvirnik pa številke vrstic prestavljenega. Zato je vsak člen vključen v determinanto prvotne matrike in determinanto, ki je transponirana z istim faktorjem

Dva nabora lastnosti kažeta, da so v kvalifikatorju vrstice in stolpci popolnoma enaki. Zato vse nadaljnje lastnosti, nastavljene za vrstice, ostanejo resnične za stolpce.

Naslednji dve lastnosti pomenita linearnost determinante glede na elemente katere koli njene črte.

3. Če so elementi katere koli premice predstavljeni kot vsota dveh členov, potem je determinanta enaka vsoti dveh determinant, v prvi od katerih so elementi označene črte enaki prvemu seštevancu, v drugem - do drugega.

Ta lastnost postane bolj pregledna, če preidemo z besedne formulacije na formulo:

Dokaz.

Jasno je, da je prva vsota enaka, druga pa enaka

Ta lastnost je seveda posplošena na primer, ko so elementi vrstice predstavljeni kot vsota več izrazov.

4. Če imajo vsi elementi katere koli vrstice determinante skupen faktor, potem lahko ta skupni faktor vzamemo iz predznaka determinante.

res,

5. Determinanta z dvema enakima nizoma je nič.

6. Če se v matriki zamenjata dve vrstici, bo njena determinanta spremenila predznak v nasprotni.

Ti dve lastnosti sta tesno povezani in igrata posebno pomembno vlogo v teoriji determinant.

Dokažimo najprej 5. lastnost, nato 6. lastnost.

Naj je determinanta podana z dvema enakima nizoma:

Vsoto razdelimo na dva dela, ki ustrezata lihi in sodi permutaciji:

Spomnimo se, da so vse lihe permutacije pridobljene, če je enaka transpozicija izvedena v vseh sodih permutacijah.

Ampak . Zato je za vsak člen v prvi vsoti enak člen v drugem, tako da je bilo treba to dokazati.

Obrnimo se zdaj na dokaz lastnosti in označimo permutirane nize preprosto z I in II. Primerjati moramo determinante

V ta namen upoštevajte pomožno determinanto, ki je a priori enaka nič:

Lastnino 3 smo uporabili dvakrat.

Prvi in ​​četrti člen sta enaka nič. Posledično je vsota drugega in tretjega enaka nič, kot je potrebno.

Razmislite o drugem načinu dokazovanja lastnosti 5 in 6. Začnimo s šestim. Naj bo

Iz druge determinante vzemite kateri koli izraz, zapisan po vrstnem redu njegovih vrstic:

Vključen je z množiteljem. Toda tako vstopi v A z množiteljem. Jasno je, da tako, da vsak člen iz A vstopi v A z nasprotnim predznakom, t.j.

Zdaj, da dokažete lastnost 5, upoštevajte determinanto z dvema enakima nizoma in obrnite te nize. Po eni strani bo hkrati spremenil znak, a se hkrati ne bo spremenil. Zato ,.

To sklepanje pa velja le, če je v obroču možno deljenje z 2, zato izhaja iz

Na področju ostankov po modulu 2 takšnega zaključka nismo mogli narediti. To je manjša pomanjkljivost drugega dokaza v primerjavi s prvim.

7. Determinanta z dvema proporcionalnima vrsticama je nič.

Dejansko, če v skladu z lastnostjo 4 vzamemo koeficient sorazmernosti onkraj predznaka determinante, potem ostane determinanta z enakimi črtami, ki je enaka nič.

8. Določevalec se ne spremeni, če v katero koli od njenih vrstic dodate števila, sorazmerna drugi vrstici.

res,

Lastnost 8 je še posebej pomembna, ker zagotavlja ključ za izračun determinant.

Poglejmo si majhen primer.

Naj je potrebno izračunati determinanto

V drugo vrstico dodajte prvo, pomnoženo z -1, nato dodajte prvo, pomnoženo z -1 k tretji, in nato prvo, pomnoženo z -1, dodajte četrti. Dobimo enako determinanto

Zdaj dodajte v četrto vrstico tretjo, pomnoženo z -1, v četrto vrstico pa drugo, pomnoženo z -1.

Dobimo enako determinanto

Zdaj se izkaže, da je samo eden od 24 členov determinante nenič:. Permutacija (1, 3, 2, 4) je liha, zato je determinanta -16.