복소변수 z의 선형함수는 a와 6에 복소수가 주어지고 a Ф 0인 형태의 함수이다. 선형함수는 독립변수 z의 모든 값에 대해 정의되며, 단일값이고 , 역함수도 단일 값이므로 전체 평면 z에서 1가입니다. 선형 함수는 전체 복소 평면에서 분석적이므로 그 도함수는 전체 평면에서 수행된 매핑과 일치합니다. 선형 분수 함수는 주어진 복소수 형식의 함수이며, 선형 분수 함수는 z = -|를 제외한 독립 변수 zy의 모든 값에 대해 정의되며 단일 값이며, 역함수이므로 함수 복소수 변수의 기본 기능 분수-합리 함수 거듭제곱 함수 지수 함수 대수 함수 삼각 및 쌍곡선 함수는 단일 값이며 점 z를 제외한 전체 복소 평면에서 1가 = - 이 영역에서 함수 (3)은 다음과 같습니다. 분석 및 그 파생물에 따라 수행되는 매핑은 등각입니다. 점 z = - \에서 함수 (3)을 확장하고 t) = oo로 설정하고 점 z(oo) =에 대응하여 무한대 w = oo에 점을 둡니다. 그러면 선형 분수 함수는 1가가 됩니다. 확장된 복소 평면 z에서. 예 1. 선형 분수 함수를 고려하십시오 평등에서 복소수 r과 u의 계수는 관계에 의해 관련되며 이러한 숫자 자체는 점 O에서 나오는 광선에 위치하며 실제 축에 대해 대칭입니다. 특히 단위원 |z| = 1 단위원 N = 1의 점으로 이동합니다. 이 경우 복소수에 켤레 번호가 할당됩니다(그림 11). 또한 함수 r0 = -g는 무한대 r - oo의 점을 0 r0 - 0에 매핑합니다. 2.2. 거듭제곱 함수 n이 자연수인 거듭제곱 함수는 전체 복소 평면에서 해석적입니다. 그것의 도함수 = nzn~] for η > 1은 z = 0을 제외한 모든 점에서 0이 아닙니다. 공식 (4)에서 w와 z를 지수 형식으로 쓰면 다음을 얻습니다. 공식 (5)에서 복소수는 k가 정수인 경우 숫자 Z\ 및 z2는 한 점 w로 이동합니다. 따라서 n > 1의 경우 매핑(4)은 z 평면에서 1가가 아닙니다. 매핑 ri = zn이 1가인 도메인의 가장 간단한 예는 a가 실수인 섹터입니다. 영역 (7)에서 매핑 (4)는 등각입니다. - 각 복소수 z \u003d r1v Ф 0에 대해 n차수가 z와 같도록 n개의 다른 복소수를 지정할 수 있기 때문에 다중 값입니다. 복소수 변수 z의 차수 n의 다항식은 a 주어진 복소수 및 ao Ф 0. 모든 차수 다항식은 전체 복소 평면에 대한 분석 함수입니다. 2.3. 분수 유리 함수 분수 유리 함수는 다음 형식의 함수입니다. 여기서)는 복소수 변수 z의 다항식입니다. 분수 유리 함수는 분모 Q(z)가 사라지는 점을 제외하고 전체 평면에서 분석적입니다. 예 3. Zhukovsky 함수는 점 z = 0을 제외한 전체 평면 z에서 해석적입니다. 이 영역에서 고려되는 Zhukovsky 함수가 1가가 되는 복소 평면 영역의 조건을 알아보겠습니다. M 점 Z)와 zj를 함수 (8)에 의해 한 점으로 옮기도록 하십시오. 따라서, 에 대해, 우리는 Zhukovsky 함수의 univalence에 대해 조건이 충족되는 것이 필요하고 충분하다는 것을 얻습니다. univalence 조건 (9)를 충족하는 도메인의 예는 원 |z| > 1. Zhukovsky 함수의 도함수 복소수 변수의 기본 함수 분수-합리 함수 거듭제곱 함수 지수 함수 대수 함수 삼각 함수와 쌍곡선 함수는 점을 제외하고 모든 곳에서 0이 아니므로 이 함수에 의해 수행되는 영역의 매핑은 다음과 같습니다. 등각(그림 13). 단위 디스크 |I의 내부는 Zhukovsky 함수의 univalence 영역이기도 합니다. 쌀. 13 2.4. 지수 함수 임의의 복소수 z = x + y에 대한 지수 함수 ez를 다음과 같이 정의합니다. x = 0에 대해 오일러 공식을 얻습니다. 지수 함수의 주요 속성을 설명하겠습니다. 1. 실수 z의 경우 이 정의 평소와 일치합니다. 이것은 공식 (10)에서 y = 0을 설정함으로써 직접 확인할 수 있습니다. 2. 함수 ez는 전체 복소 평면에 대해 해석적이며, 이에 대해 일반적인 미분 공식이 유지됩니다. 3. 함수 ez에 대해 덧셈 정리가 유지됩니다. . 4. 함수 ez는 가상의 주 주기가 2xi인 주기적입니다. 실제로, 임의의 정수 k에 대해 다른 한편으로, 정의 (10)에서 그것은 다음을 따른다. 스트립은 관계식(12)과 관련된 단일 쌍의 점을 포함하지 않으므로 연구 결과 w = e" 매핑이 스트립에서 1가라는 결과가 나옵니다(그림 14). 파생물이므로 이 매핑은 다음과 같습니다. 참고 niv 함수 rg는 모든 스트립에서 1가 가치 함수는 대수라고 하며 다음과 같이 표시됩니다. 그러면 Ln z에 대해 공식 2가 얻어집니다. 6. 삼각 함수 및 쌍곡선 함수 실수 y에 대한 오일러 공식 (11)에서 우리는 다음 공식을 사용하여 복소수 z에 대한 삼각 함수 sin z 및 cos z를 정의합니다. 복소수 인수의 사인 및 코사인에는 흥미로운 속성이 있습니다. . 주요 내용을 나열해 보겠습니다. 함수 sinz 및 cos z: 1) 실수 z -x의 경우 일반적인 사인 및 코사인과 일치합니다. 2) 복잡한 평면 전체에 대해 분석적입니다. 3) 일반적인 미분 공식을 따릅니다. 4) 주기가 2n인 주기입니다. 5) sin z - 홀수 함수, cos z - 짝수; 6) 일반적인 삼각 관계가 유지됩니다. 나열된 모든 속성은 공식 (15)에서 쉽게 얻을 수 있습니다. 복소수 영역의 함수 tgz 및 ctgz는 공식으로 정의되며 쌍곡선 함수는 "쌍곡선 함수는 삼각 함수와 밀접하게 관련되어 있습니다. 이 관계는 다음 등식으로 표현됩니다. 복소수 인수의 사인 및 코사인은 다음을 갖습니다. 또 다른 중요한 속성: 복잡한 평면에서 | \ 임의로 큰 양수 속성 6과 공식 (18)을 사용하여 복합 변수의 기본 함수 분수-합리 함수 거듭제곱 함수 지수 함수 로그 함수 삼각 함수 및 쌍곡선 함수 예제 4. -4 ,

복잡한 변수의 기능.
복잡한 변수의 기능 미분.

이 기사는 복잡한 변수의 기능 이론과 관련된 일반적인 문제를 고려할 일련의 수업을 시작합니다. 예제를 성공적으로 마스터하려면 복소수에 대한 기본 지식이 있어야 합니다. 자료를 통합하고 반복하려면 페이지를 방문하는 것으로 충분합니다. 찾는 기술도 필요합니다. 2차 편도함수. 여기, 이러한 편도함수가 있습니다 ... 지금도 나는 그들이 얼마나 자주 발생하는지 조금 놀랐습니다 ...

우리가 분석하기 시작하는 주제는 특별히 어렵지 않으며, 복잡한 변수의 기능에서는 원칙적으로 모든 것이 명확하고 접근 가능합니다. 가장 중요한 것은 경험적으로 파생된 기본 규칙을 준수하는 것입니다. 읽어!

복잡한 변수의 함수 개념

먼저 한 변수의 학교 함수에 대한 지식을 새로 고침해 보겠습니다.

한 변수의 기능정의 영역에서 독립 변수의 각 값이 함수의 단 하나의 값에 해당하는 규칙입니다. 당연히 "x"와 "y"는 실수입니다.

복잡한 경우에 기능적 종속성은 유사하게 주어집니다.

복합 변수의 단일 값 함수모두가 지켜야 하는 규칙이다 통합(도메인에서) 독립 변수의 값은 단 하나에 해당합니다. 포괄적 인함수 값. 이론상으로는 다중값 함수 및 일부 다른 유형의 함수도 고려되지만 단순화를 위해 하나의 정의에 중점을 둘 것입니다.

복잡한 변수의 기능은 무엇입니까?

가장 큰 차이점은 숫자가 복잡하다는 것입니다. 나는 아이러니하지 않습니다. 그러한 질문에서 그들은 종종 혼미에 빠지며 기사의 끝에서 멋진 이야기를 할 것입니다. 수업에서 인형을 위한 복소수우리는 형식의 복소수를 고려했습니다. 지금부터 문자 "Z"는 변하기 쉬운, 우리는 그것을 다음과 같이 나타낼 것입니다: , "x"와 "y"는 다른 것을 취할 수 있습니다 유효한가치. 대략적으로 말하면 복합 변수의 기능은 "일반적인" 값을 취하는 변수 및 에 따라 달라집니다. 이 사실로부터 논리적으로 다음과 같은 점이 도출된다.

복잡한 변수의 기능은 다음과 같이 작성할 수 있습니다.
, 여기서 및는 2의 두 함수입니다. 유효한변수.

함수가 호출됩니다 실제 부분기능 .
함수가 호출됩니다 허수부기능 .

즉, 복소수 변수의 함수는 두 개의 실제 함수와 에 의존합니다. 마지막으로 모든 것을 명확히 하기 위해 실제 예를 살펴보겠습니다.

실시예 1

해결책:기억하는 것처럼 독립 변수 "z"는 , 따라서 다음과 같이 작성됩니다.

(1) 원래 기능으로 대체됩니다.

(2) 첫 번째 항에는 기약 곱셈 공식을 사용했습니다. 기간 동안 브래킷이 열렸습니다.

(3) 조심스럽게 제곱하여 다음을 잊지 마십시오.

(4) 용어의 재배열: 첫 번째 용어 재작성 , 허수 단위가 없는 경우(첫 번째 그룹), 다음이 있는 곳에서 용어 (두 번째 그룹). 용어를 섞을 필요는 없으며 이 단계는 건너뛸 수 있습니다(실제로는 구두로 수행).

(5) 두 번째 그룹은 대괄호에서 제외됩니다.

결과적으로 우리의 기능은 다음과 같은 형식으로 표현되었습니다.

대답:
함수의 실제 부분입니다.
함수의 허수 부분입니다.

이러한 기능은 무엇입니까? 두 변수의 가장 일반적인 함수, 그 중에서 인기 있는 부분 파생 상품. 자비 없이 - 우리는 찾을 것입니다. 하지만 조금 후에.

간단히 말해서, 해결된 문제의 알고리즘은 다음과 같이 작성할 수 있습니다. 우리는 원래 기능으로 대체하고, 단순화를 수행하고, 모든 항을 허수 단위(실수부)가 없고 허수부(허수부)가 있는 두 그룹으로 나눕니다.

실시예 2

함수의 실수부와 허수부 찾기

이것은 DIY의 예입니다. 체커를 벗은 채로 복잡한 비행기에서 전투에 임하기 전에 이 주제에 대한 가장 중요한 조언을 드리겠습니다.

조심 해요!물론 모든 곳에서 조심해야하지만 복소수에서는 그 어느 때보 다 조심해야합니다! 브래킷을 조심스럽게 확장하고 아무것도 잃지 않도록 하십시오. 내 관찰에 따르면 가장 흔한 실수는 부호를 잃는 것입니다. 서두르지 마!

수업이 끝날 때 완전한 솔루션과 답변.

이제 큐브입니다. 약식 곱셈 공식을 사용하여 다음을 도출합니다.
.

공식은 솔루션 프로세스의 속도를 크게 향상시키기 때문에 실제로 사용하기에 매우 편리합니다.

복잡한 변수의 기능 미분.

좋은 소식과 나쁜 소식 두 가지가 있습니다. 좋은 것부터 시작하겠습니다. 복잡한 변수의 함수에 대해서는 미분 규칙과 기본 함수의 도함수 표가 유효합니다. 따라서 도함수는 실수 변수의 함수의 경우와 정확히 같은 방식으로 취해집니다.

나쁜 소식은 복잡한 변수의 많은 기능에 대해 도함수가 전혀 없으며 미분 가능하다하나의 기능 또는 다른 기능. 그리고 당신의 마음이 어떻게 느끼는지 "파악"하는 것은 추가적인 문제와 관련이 있습니다.

복잡한 변수의 함수를 고려하십시오. 이 함수를 미분할 수 있으려면 다음이 필요하고 충분합니다.

1) 1차의 편도함수가 있어야 합니다. 복잡한 변수의 기능 이론에서 전통적으로 다른 버전의 표기법이 사용되기 때문에 이러한 표기법은 즉시 잊어버리십시오. .

2) 소위 수행하기 위해 코시-리만 조건:

이 경우에만 파생 상품이 존재합니다!

실시예 3

해결책연속적인 세 단계로 분해:

1) 함수의 실수부와 허수부를 찾습니다. 이 작업은 이전 예에서 분석되었으므로 주석 없이 기록하겠습니다.

그때부터:

이런 식으로:

함수의 허수 부분입니다.

기술적인 요점을 하나 더 설명하겠습니다. 어떤 순서로실수와 허수 부분에 용어를 작성? 예, 기본적으로 중요하지 않습니다. 예를 들어 실제 부분은 다음과 같이 작성할 수 있습니다. , 그리고 상상의 - 다음과 같이: .

2) Cauchy-Riemann 조건이 성립하는지 확인해보자. 두 가지가 있습니다.

상태를 확인하는 것부터 시작하겠습니다. 우리는 찾는다 부분 파생 상품:

따라서 조건이 충족됩니다.

의심할 여지 없이, 좋은 소식은 편도함수가 거의 항상 매우 간단하다는 것입니다.

두 번째 조건의 충족 여부를 확인합니다.

그것은 같은 것으로 밝혀졌지만 반대 징후, 즉 조건도 충족되었습니다.

Cauchy-Riemann 조건이 충족되므로 함수는 미분 가능합니다.

3) 함수의 도함수를 구합니다. 도함수도 매우 간단하며 일반적인 규칙에 따라 찾습니다.

미분의 허수 단위는 상수로 간주됩니다.

대답: - 실제 부분 상상의 부분이다.
Cauchy-Riemann 조건이 충족됩니다.

파생물을 찾는 두 가지 방법이 더 있습니다. 물론 덜 자주 사용되지만 정보는 두 번째 수업을 이해하는 데 유용합니다. 복잡한 변수의 기능을 찾는 방법은 무엇입니까?

도함수는 다음 공식을 사용하여 찾을 수 있습니다.

이 경우:

이런 식으로

역 문제를 해결해야 합니다. 결과 표현식에서 를 분리해야 합니다. 이렇게 하려면 다음과 같이 괄호에서 빼야 합니다.

많은 사람들이 알아차린 것처럼 역동작은 수행하기가 다소 더 어렵습니다. 확인을 위해 항상 표현과 초안을 취하거나 구두로 괄호를 다시 열어 정확히 나오는지 확인하는 것이 좋습니다.

도함수를 찾기 위한 미러 공식:

이 경우: , 그 이유는 다음과 같습니다.

실시예 4

함수의 실수부와 허수부를 결정합니다. . Cauchy-Riemann 조건의 충족을 확인합니다. Cauchy-Riemann 조건이 충족되면 함수의 도함수를 찾습니다.

수업이 끝날 때 짧은 솔루션과 대략적인 마무리 샘플.

Cauchy-Riemann 조건이 항상 충족됩니까? 이론상으로는 실제보다 충족되지 않는 경우가 더 많습니다. 그러나 실제 예에서는 실행되지 않은 경우를 기억하지 못합니다 =) 따라서 편도함수가 "수렴하지 않은" 경우 매우 높은 확률로 어딘가에서 실수했다고 말할 수 있습니다.

우리의 기능을 복잡하게 하자:

실시예 5

함수의 실수부와 허수부를 결정합니다. . Cauchy-Riemann 조건의 충족을 확인합니다. 계산하다

해결책:솔루션 알고리즘은 완전히 보존되지만 마지막에 새로운 유행이 추가됩니다. 즉, 한 점에서 도함수를 찾는 것입니다. 큐브의 경우 필요한 공식이 이미 파생되었습니다.

이 함수의 실수부와 허수부를 정의해 보겠습니다.

주목 또 주목!

그때부터:


이런 식으로:
함수의 실제 부분입니다.
함수의 허수 부분입니다.

두 번째 조건 확인:

그것은 같은 것으로 밝혀졌지만 반대 징후, 즉 조건도 충족되었습니다.

Cauchy-Riemann 조건이 충족되므로 함수는 미분 가능합니다.

필요한 지점에서 미분 값을 계산합니다.

대답:, , 코시-리만 조건이 충족되고,

큐브가 있는 함수는 일반적이므로 통합할 예는 다음과 같습니다.

실시예 6

함수의 실수부와 허수부를 결정합니다. . Cauchy-Riemann 조건의 충족을 확인합니다. 계산하다 .

수업이 끝날 때 결정 및 샘플 마무리.

복잡한 분석 이론에서 복잡한 인수의 다른 기능(지수, 사인, 코사인 등)도 정의됩니다. 이러한 함수는 비정상적이고 심지어 기이한 속성을 가지고 있습니다. 그리고 정말 흥미롭습니다! 정말 말씀드리고 싶지만 여기에서는 참고서나 교과서가 아닌 해결 방법으로 일어난 일이므로 몇 가지 공통 기능을 사용하여 동일한 작업을 고려하겠습니다.

먼저 소위 오일러 공식:

누구에게나 유효한숫자의 경우 다음 공식이 유효합니다.

참고용으로 노트북에 복사할 수도 있습니다.

엄밀히 말하면 공식은 하나뿐이지만 일반적으로 편의상 표시기에 마이너스가있는 특수 케이스도 작성합니다. 매개변수는 단일 문자일 필요는 없으며 복잡한 표현식, 함수일 수 있습니다. 유효한가치. 사실, 우리는 지금 그것을 보게 될 것입니다:

실시예 7

파생 상품을 찾으십시오.

해결책:파티의 일반적인 라인은 흔들리지 않습니다. 기능의 실제 부분과 허수 부분을 골라낼 필요가 있습니다. 자세한 해결책을 제시하고 아래의 각 단계에 대해 설명하겠습니다.

그때부터:

(1) "z"를 대체합니다.

(2) 대입 후 실수부와 허수부를 분리해야 함 지수의 첫 번째출품자. 이렇게 하려면 브래킷을 엽니다.

(3) 표시기의 허수 부분을 그룹화하여 허수 단위를 괄호 안에 넣습니다.

(4) 권한이 있는 학교 행동을 사용합니다.

(5) 승수에 대해 오일러 공식을 사용하는 동안 .

(6) 결과적으로 괄호를 엽니다.

함수의 실제 부분입니다.
함수의 허수 부분입니다.

추가 작업은 표준입니다. Cauchy-Riemann 조건이 충족되는지 확인하겠습니다.

실시예 9

함수의 실수부와 허수부를 결정합니다. . Cauchy-Riemann 조건의 충족을 확인합니다. 그래서 우리는 파생 상품을 찾지 못할 것입니다.

해결책:솔루션 알고리즘은 앞의 두 예제와 매우 유사하지만 매우 중요한 포인트가 있으므로 초기 단계에 대해 다시 단계별로 설명하겠습니다.

그때부터:

1) "z" 대신에 대체합니다.

(2) 먼저 실수부와 허수부를 선택합니다. 부비동 내부. 이를 위해 브래킷을 엽니다.

(3) 우리는 공식을 사용하는 반면, .

(4) 사용 쌍곡선 코사인의 패리티: 그리고 쌍곡선 사인 기이함: . 쌍곡선은 이 세계에 속하지는 않지만 여러 면에서 유사한 삼각 함수와 유사합니다.

결국:
함수의 실제 부분입니다.
함수의 허수 부분입니다.

주목!빼기 기호는 허수 부분을 나타내며 어떤 경우에도 잃어 버려서는 안됩니다! 시각적 설명을 위해 위에서 얻은 결과를 다음과 같이 다시 작성할 수 있습니다.

Cauchy-Riemann 조건의 충족을 확인합시다.

Cauchy-Riemann 조건이 충족됩니다.

대답:, , 코시-리만 조건을 만족합니다.

코사인, 신사 숙녀 여러분, 우리는 스스로 다음을 이해합니다.

실시예 10

함수의 실수부와 허수부를 결정합니다. Cauchy-Riemann 조건의 충족을 확인합니다.

나는 모든 사람이 껍질을 벗긴 땅콩과 같은 것을 다룰 수 있기 때문에 의도적으로 더 복잡한 예를 골랐습니다. 동시에 주의력을 훈련하십시오! 수업이 끝나면 호두까기 인형.

글쎄, 결론적으로 나는 복잡한 인수가 분모에있을 때 또 다른 흥미로운 예를 고려할 것입니다. 실전에서 몇 번 만났으니 간단한 것을 분석해보자. 아 늙어간다...

실시예 11

함수의 실수부와 허수부를 결정합니다. Cauchy-Riemann 조건의 충족을 확인합니다.

해결책:다시 말하지만, 함수의 실수부와 허수부를 분리해야 합니다.
그렇다면

질문이 생깁니다. "Z"가 분모에 있을 때 어떻게 해야 합니까?

모든 것이 간단합니다. 표준이 도움이 될 것입니다. 분자와 분모에 켤레식을 곱하는 방법, 수업의 예에서 이미 사용되었습니다. 인형을 위한 복소수. 학교 공식을 기억합시다. 분모에는 이미 있으므로 켤레 표현식은 입니다. 따라서 분자와 분모에 다음을 곱해야 합니다.

11 복잡한 변수의 기본 기능

복소수 지수의 정의를 상기하십시오 - . 그 다음에

Maclaurin 시리즈 확장. 이 급수의 수렴 반경은 +∞이며, 이는 복소 지수가 전체 복소 평면에 대해 해석적임을 의미하며,

(exp z)"=exp z; exp 0=1. (2)

여기에서 첫 번째 평등은 예를 들어 거듭제곱 급수의 항 별 미분에 대한 정리에서 따릅니다.

11.1 삼각함수와 쌍곡선 함수

복소수 변수의 사인함수라고 하는

복소수 변수의 코사인기능이 있다

복소수 변수의 쌍곡사인다음과 같이 정의됩니다.

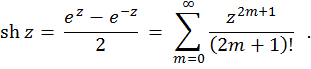
복소수 변수의 쌍곡코사인-- 함수입니다

새로 도입된 기능의 몇 가지 속성에 주목합니다.

ㅏ. x∈ ℝ이면 cos x, sin x, ch x, sh x∈ ℝ입니다.

비.삼각 함수와 쌍곡선 함수 사이에는 다음과 같은 연결이 있습니다.

cos iz=ch z; sin iz=ish z, ch iz=cos z; 시즈=이신즈.

B. 기본 삼각법 및 쌍곡선 아이덴티티:

cos 2 z+sin 2 z=1; 채널 2 z-sh 2 z=1.

기본 쌍곡선 ID의 증거입니다.

삼각함수와 쌍곡선 함수 사이의 연결을 고려할 때 주요 삼각법 항등은 Ononian 쌍곡선 항등에서 따릅니다(속성 B 참조).

G 덧셈 공식:

특히,

디.삼각 함수와 쌍곡선 함수의 도함수를 계산하려면 거듭제곱 급수의 항별 미분에 대한 정리를 적용해야 합니다. 우리는 다음을 얻습니다:

(cos z)"=-sin z; (sin z)"=cos z; (chz)"=shz; (shz)"=chz.

이자형.함수 cos z, ch z는 짝수이고 함수 sin z, sh z는 홀수입니다.

G. (주기성)함수 e z는 주기가 2π i인 주기적입니다. 함수 cos z, sin z는 주기가 2π인 주기적이고 함수 ch z, sh z는 주기가 2πi인 주기입니다. 게다가,

합계 공식을 적용하면 다음을 얻습니다.

여. 실수부와 허수부로 분해:

단일 값 분석 함수 f(z)가 도메인 D를 도메인 G에 전단사적으로 매핑하는 경우 D를 univalence 도메인이라고 합니다.

그리고.도메인 D k =( x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .

증거. 관계식 (5)는 매핑 exp:D k → ℂ가 주입임을 의미합니다. w를 0이 아닌 복소수라고 하자. 그런 다음 방정식을 풀면 e x =|w| 및 e iy =w/|w| 실제 변수 x 및 y 사용(절반 간격에서 y 선택)