결정적인 속성. 행렬식의 순서 줄이기

일부 일치하는 것이 가능합니다. 숫자, 특정 규칙에 따라 계산되고 호출됨 결정자.

개념 도입의 필요성 결정자 - 번호특성화 정사각형주문 행렬 N , 선형 대수 방정식 시스템의 솔루션과 밀접하게 관련되어 있습니다.

행렬 행렬식 ㅏ다음을 나타냅니다. | ㅏ| 또는 D.

1차 행렬의 행렬식ㅏ = (ㅏ 11) 호출된 요소 ㅏ열하나 . 예를 들어, ㅏ= (-4) 우리는 | ㅏ| = -4.

2차 행렬 행렬식~라고 불리는 숫자, 공식에 의해 결정

|ㅏ| = .

예를 들어, | ㅏ| = .

즉, 이 규칙은 다음과 같이 작성할 수 있습니다. 기호가 있는 경우 연결된 요소의 곱을 가져와야 합니다. 주 대각선, 그리고 삼각형의 꼭짓점에 의해 연결된 요소의 곱, 주 대각선에 평행한 밑변. 유사한 제품은 보조 대각선에 대해서만 반대 기호로 사용됩니다.

예를 들어,

행렬 행렬식의 정의 N우리는 th 명령을주지 않고 그것을 찾는 방법 만 보여줍니다.

나중에는 말 대신 행렬 행렬식 N-번째 주문그냥 얘기하자 결정자 N-번째 주문. 새로운 개념을 소개하겠습니다.

정방행렬이 주어질 때 N-번째 주문.

미성년자중 ij 요소 ㅏ ij 행렬 ㅏ~라고 불리는 결정자 (N-1) 행렬에서 얻은 차수 ㅏ삼진 나-번째 줄과 제이-번째 열.

행렬 A의 요소 a ij의 대수 보수 A ij는 부호 (-1) i+j로 취한 소수입니다.

ㅏ ij = (-1) 나는 + j 중아이고,

저것들. 대수적 보수는 행과 열의 합이 짝수일 때 소수와 일치하거나 행과 열의 합이 홀수일 때 부호가 다릅니다.

예를 들어 요소의 경우 ㅏ 11 및 ㅏ 12개의 행렬 A = 미성년자

중 11 = ㅏ 11 = ,

중 12 = ,

ㅏ ㅏ 12 = (-1) 1+2 중 12 = -8.

정리(행렬의 분해에 관하여) . 정방 행렬의 행렬식은 모든 행(열)의 요소와 대수 보수의 곱의 합과 같습니다. 즉,

|ㅏ| = ㅏ i1 ㅏ i1 + ㅏ i2 ㅏ i2 + … + ㅏ~에 ㅏ에 ,
누구에게나 나 = 1, 2, …, N

|ㅏ| = ㅏ 1j ㅏ 1j+ ㅏ 2j ㅏ 2j + … + ㅏ뉴저지 ㅏ뉴저지 ,

누구에게나 제이 = 1, 2, …, N

첫 번째 공식은 나-번째 줄,그리고 두 번째 - 요소에 의한 행렬식 분해 제이-번째 열.

이 공식의 도움으로 모든 행렬식을 이해하는 것은 쉽습니다. N-차수는 행렬식의 합으로 축소될 수 있으며, 그 차수는 1이 되는 식입니다. 3차 또는 2차 행렬식에 도달할 때까지 계산이 더 이상 어렵지 않습니다.

행렬식을 찾기 위해 다음과 같은 기본 속성을 적용할 수 있습니다.

1. 행렬식의 행(또는 열)이 0으로 구성된 경우 행렬식 자체는 0과 같습니다.

2. 두 개의 행(또는 두 개의 열)을 치환할 때 행렬식에 -1을 곱합니다.

3. 두 개의 동일하거나 비례하는 행(또는 열)이 있는 행렬식은 0과 같습니다.

4. 행(또는 열) 요소의 공통 인수는 행렬식의 부호에서 제거할 수 있습니다.

5. 모든 행과 열이 바뀌더라도 행렬식의 값은 변경되지 않습니다.

6. 다른 행(열)에 숫자를 곱한 값이 행 중 하나(또는 열 중 하나)에 추가되더라도 행렬식의 값은 변경되지 않습니다.

7. 행렬의 행(또는 열) 요소의 곱과 이 행렬의 다른 행(열) 요소의 대수 보수의 합은 0입니다.

8. 두 개의 제곱 행렬 곱의 행렬식은 행렬식의 곱과 같습니다.

행렬 행렬식의 개념을 도입하면 행렬을 사용하여 역행렬을 찾는 연산을 한 번 더 정의할 수 있습니다.

0이 아닌 모든 숫자에 대해 이 숫자의 곱이 1을 제공하는 역수가 있습니다. 정사각형 행렬에 대한 이러한 개념도 있습니다.

행렬 ㅏ-1 호출 뒤집다...쪽으로 정사각형행렬 ㅏ, 오른쪽과 왼쪽 모두에서 이 행렬에 주어진 행렬을 곱하면 다음을 얻습니다. 단위 행렬, 즉.

ㅏ× ㅏ -1 = ㅏ-1× ㅏ= 이자형.

정방 행렬만이 역행렬을 갖는다는 정의에 따릅니다. 이 경우 역행렬은 같은 차수의 제곱이 됩니다. 그러나 모든 정방 행렬에 역행렬이 있는 것은 아닙니다.

대수 덧셈과 부전공

3차 행렬식이 있다고 합시다. .

미성년자이 요소에 해당 아이즈 3차 행렬식은 주어진 요소가 교차하는 행과 열을 삭제하여 주어진 요소에서 얻은 2차 행렬식이라고 합니다. 나-번째 줄과 제이-번째 열. 주어진 요소에 해당하는 미성년자 아이즈우리는 표시 할 것입니다 미지.

예를 들어, 미성년자 M12요소에 해당 12, 결정 요인이 있을 것입니다. 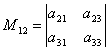, 주어진 행렬식에서 첫 번째 행과 두 번째 열을 삭제하여 얻습니다.

따라서 3차 행렬식을 결정하는 공식은 이 행렬식이 첫 번째 행의 요소와 해당하는 소수 요소의 곱의 합과 같다는 것을 보여줍니다. 요소에 해당하는 미성년자 12, "-" 기호와 함께 사용됩니다. 라고 쓸 수 있다

(1)

유사하게, 2차 이상의 행렬식에 대한 미성년자의 정의를 도입할 수 있습니다.

개념을 하나 더 소개하겠습니다.

대수 덧셈요소 아이즈행렬식을 소수라고 합니다. 미지(-1) i+j 를 곱합니다.

대수 요소 추가 아이즈표시된 아이즈.

정의에서 우리는 요소의 대수적 보수와 그 소수 사이의 연결이 평등으로 표현된다는 것을 얻습니다. 아이즈= (-1) i+j 미지 .

예를 들어,

예시.주어진 행렬식. 찾다 A 13 , A 21 , A 32.

요소의 대수적 덧셈을 사용하여 공식 (1)을 다음과 같이 작성할 수 있음을 쉽게 알 수 있습니다.

이 공식과 유사하게, 행이나 열의 요소에 대한 행렬식의 분해를 얻을 수 있습니다.

예를 들어, 두 번째 행의 요소에 대한 행렬식의 분해는 다음과 같이 얻을 수 있습니다. 행렬식의 속성 2에 따르면 다음과 같습니다.

얻은 행렬식을 첫 번째 행의 요소로 확장해 보겠습니다.

(2)

여기에서 왜냐하면 식 (2)의 2차 행렬식은 원소의 소수이다. 21, 22, 23. 따라서, 즉 우리는 두 번째 행의 요소에 의해 행렬식의 확장을 얻었습니다.

유사하게, 세 번째 행의 요소에 대한 행렬식의 분해를 얻을 수 있습니다. 행렬식의 속성 1(전치 시)을 사용하여 유사한 확장이 열 요소의 확장에도 유효함을 보여줄 수 있습니다.

따라서 다음 정리는 참입니다.

정리(주어진 행 또는 열에서 행렬식 확장 시).행렬식은 행(또는 열)의 요소와 대수적 보수의 곱의 합과 같습니다.

위의 모든 것은 더 높은 차수의 행렬식에 대해 사실입니다.

예.

역행렬

역행렬의 개념은 다음에 대해서만 소개됩니다. 정사각형 행렬.

만약에 ㅏ는 정사각 행렬이고, 뒤집다그것을 위해 행렬은 다음으로 표시된 행렬입니다. A-1그리고 조건을 만족합니다. (이 정의는 숫자의 곱셈과 유추하여 도입되었습니다)

속성 1. 모든 행이 열로 대체되고 각 행이 동일한 번호의 열로 대체되는 경우 행렬식의 값은 변경되지 않습니다.

속성 2. 행렬식의 두 열 또는 두 행을 치환하는 것은 -1을 곱하는 것과 같습니다. 예를 들어,

속성 3. 행렬식에 두 개의 동일한 열 또는 두 개의 동일한 행이 있으면 0과 같습니다.

속성 4. 행렬식의 한 열 또는 한 행의 모든 요소에 임의의 수 k를 곱하는 것은 행렬식에 이 수 k를 곱하는 것과 같습니다. 예를 들어,

속성 5. 일부 열 또는 일부 행의 모든 요소가 0이면 행렬식 자체는 0과 같습니다. 이 속성은 이전 속성의 특수한 경우입니다(k=0인 경우).

속성 6. 행렬식의 두 열 또는 두 행의 해당 요소가 비례하면 행렬식은 0과 같습니다.

속성 7. 행렬식의 n번째 열 또는 n번째 행의 각 요소가 두 항의 합인 경우 행렬식은 n번째 열 또는 각각 n번째 열에 있는 두 행렬식의 합으로 나타낼 수 있습니다. 행에는 언급 된 용어의 첫 번째 항목이 있고 다른 항목에는 두 번째 항목이 있습니다. 나머지 위치의 요소는 세 결정자의 이정표에 대해 동일합니다. 예를 들어,

속성 8. 일부 열(또는 일부 행)의 요소에 다른 열(또는 다른 행)의 해당 요소를 추가하고 공통 요소를 곱하면 행렬식의 값은 변경되지 않습니다. 예를 들어,

행렬식의 추가 속성은 대수 보수 및 소수의 개념과 연결됩니다. 어떤 요소의 마이너는 주어진 요소에서 이 요소가 위치한 교차점의 행과 열을 삭제하여 얻은 행렬식입니다.

행렬식의 모든 요소의 대수 보수는 요소가 위치한 교차점의 행 및 열 번호의 합이 짝수이고 반대인 경우 부호와 함께 취한 이 요소의 소수와 같습니다. 이 숫자가 홀수이면 부호를 붙입니다.

요소의 대수적 보수를 요소 자체를 나타내는 문자와 동일한 이름 및 동일한 숫자의 대문자로 표시합니다.

속성 9. 결정자

열(또는 행)의 요소와 대수적 보수의 곱의 합과 같습니다.

즉, 다음과 같은 평등이 성립합니다.

, ,

, .

6) 미성년자 및 대수 추가.

정의. 행렬식의 소수 요소는 th입니다. 주문하다~라고 불리는 결정자- 주어진 명령에서 얻은 차수 결정자요소가 교차하는 -번째 행과 -번째 열을 삭제합니다.

명칭: .

정의. -th 차수의 행렬식 요소의 대수적 보수는 짝수이면 더하기 기호로, 그렇지 않으면 빼기 기호로 취한 소수입니다.

명칭: .

정리. (식의 확장에 대해.)

행렬식은 행렬식의 행(또는 열) 요소와 대수적 보수의 곱의 합과 같습니다.

7) 역행렬- 그런 행렬 ㅏ −1 , 곱하면 원래 행렬 ㅏ결과적으로 준다 단위 행렬 이자형:

정방행렬축퇴되지 않은 경우에만 가역적입니다. 결정자 0과 같지 않습니다. 정사각형이 아닌 행렬의 경우 퇴화 행렬역행렬은 존재하지 않습니다. 그러나 이 개념을 일반화하고 소개하는 것은 가능합니다. 유사 역행렬, 많은 속성의 역함수와 유사합니다.

8)매트릭스 순위- 가장 높은 차수 미성년자이 행렬, 0이 아닌

일반적으로 행렬의 순위는 () 또는 . 두 명칭 모두 외국어에서 우리에게 왔으므로 둘 다 사용할 수 있습니다.

속성

정리(마이너 기준): r = rang AM을 행렬 A의 마이너 기준이라고 하면 다음과 같습니다.

기본 행과 기본 열은 선형 독립적입니다.

행렬 A의 모든 행(열)은 기본 행(열)의 선형 조합입니다.

- 새를 죽음에 이르게 하라!
자유가 그녀를 걱정하게하십시오!
그리고 배는 항해 중이고 원자로는 굉음...
- 파시, 고집이 센거야?

8학년 전에는 대수학을 좋아하지 않았던 걸로 기억합니다. 전혀 마음에 들지 않았습니다. 그녀는 나를 화나게 했다. 아무것도 이해하지 못했기 때문입니다.

그리고 하나의 칩을 잘라냈기 때문에 모든 것이 바뀌었습니다.

일반적으로 수학(특히 대수학)에서 모든 것은 유능하고 일관된 정의 체계를 기반으로 합니다. 당신은 정의를 알고, 그 본질을 이해합니다. 나머지를 이해하는 것은 어렵지 않을 것입니다.

그것이 오늘 수업의 주제입니다. 행렬, 행렬식 및 모든 속성을 완전히 다룰 수 있는 몇 가지 관련 문제와 정의를 자세히 고려할 것입니다.

행렬식은 행렬 대수학의 중심 개념입니다. 축약된 곱셈 공식과 마찬가지로, 고급 수학 과정을 통해 당신을 괴롭힐 것입니다. 그러므로 우리는 철저히 읽고, 보고, 이해합니다. :)

그리고 우리는 가장 친밀한 것부터 시작할 것입니다. 행렬이란 무엇입니까? 그리고 그것을 사용하는 방법.

행렬에서 인덱스의 올바른 배치

행렬은 숫자로 채워진 테이블일 뿐입니다. 네오는 여기에 없습니다.

행렬의 주요 특성 중 하나는 차원입니다. 구성되는 행과 열의 수입니다. 행렬 $A$는 $m$ 행과 $n$ 열이 있는 경우 일반적으로 $\left[ m\times n \right]$ 크기를 갖는다고 합니다. 다음과 같이 작성하십시오.

또는 다음과 같이:

다른 명칭이 있습니다. 모두 강사 / 신학생 / 교과서 저자의 선호도에 달려 있습니다. 그러나 어쨌든 이러한 모든 $\left[ m\times n \right]$ 및 $((a)_(ij))$에 대해 동일한 문제가 발생합니다.

어떤 인덱스가 어떤 역할을 합니까? 행 번호가 먼저이고 열 번호가 먼저입니까? 혹은 그 반대로도?

강의와 교과서를 읽으면 답이 뻔히 보입니다. 하지만 시험장에 과제가 있는 시트만 있으면 걱정이 되기도 하고 갑자기 헷갈릴 수도 있습니다.

따라서 이 문제를 한 번에 처리해 보겠습니다. 먼저 학교 수학 과정의 일반적인 좌표계를 기억해 보겠습니다.

평면의 좌표계 도입

그녀를 기억하십니까? $x$ 및 $y$ 축의 원점(포인트 $O=\left(0;0 \right)$)이 있으며 평면의 각 포인트는 좌표에 의해 고유하게 결정됩니다. $A=\left( 1;2 \ right)$, $B=\left(3;1 \right)$ 등

이제 이 구성을 가져와 행렬 옆에 놓아 원점이 왼쪽 상단 모서리에 오도록 합시다. 왜 거기? 예, 책을 열 때 페이지의 왼쪽 상단 모서리부터 읽기 시작하기 때문입니다. 기억하는 것이 그 어느 때보다 쉽습니다.

그러나 축을 어디로 향할 것인가? 전체 가상 "페이지"가 이러한 축으로 덮이도록 지시할 것입니다. 사실, 이를 위해서는 좌표계를 회전해야 합니다. 이 위치에 대해 가능한 유일한 옵션:

좌표계를 행렬에 매핑

이제 행렬의 모든 셀에는 단일 값 좌표 $x$ 및 $y$가 있습니다. 예를 들어 $((a)_(24))$ 항목은 $x=2$ 및 $y=4$ 좌표로 요소에 액세스하고 있음을 의미합니다. 행렬의 차원은 숫자 쌍으로 고유하게 지정됩니다.

행렬의 인덱스 정의

이 사진을 자세히 살펴보십시오. 좌표를 가지고 놀아보세요(특히 실제 행렬과 행렬식으로 작업할 때). 그러면 곧 가장 복잡한 정리와 정의에서도 무엇이 문제인지 완벽하게 이해하고 있다는 것을 깨닫게 될 것입니다.

알았어요? 자, 깨달음의 첫 번째 단계인 행렬식의 기하학적 정의로 넘어가 보겠습니다. :)

기하학적 정의

우선, 행렬식은 $\left[ n\times n \right]$ 형식의 정방 행렬에 대해서만 존재한다는 점에 주목하고 싶습니다. 행렬식은 특정 규칙에 따라 계산되는 숫자이며 이 행렬의 특성 중 하나입니다(순위, 고유 벡터와 같은 다른 특성이 있지만 다른 강의에서 더 자세히 설명합니다).

글쎄,이 기능은 무엇입니까? 무슨 뜻인가요? 간단 해:

정방 행렬 $A=\left[ n\times n \right]$ 의 행렬식은 $n$ 차원 평행 육면체의 부피이며 행렬의 행을 의 모서리를 형성하는 벡터로 간주하면 형성됩니다. 이 평행 육면체.

예를 들어, 2x2 행렬의 행렬식은 평행사변형의 면적일 뿐이며, 3x3 행렬의 경우 이미 3차원 평행육면체의 부피입니다. 스테레오메트리 수업에서 많이.

언뜻 보기에 이 정의는 완전히 부적절해 보일 수 있습니다. 그러나 결론을 서두르지 마십시오. 예를 살펴 보겠습니다. 사실 모든 것은 기본입니다. Watson:

일. 행렬 행렬식 찾기:

\[\왼쪽| \begin(행렬) 1 & 0 \\ 0 & 3 \\end(행렬) \right|\quad \left| \begin(행렬) 1 & -1 \\ 2 & 2 \\\end(행렬) \right|\quad \left| \begin(행렬)2 & 0 & 0 \\ 1 & 3 & 0 \\ 1 & 1 & 4 \\end(행렬) \right|\]

해결책. 처음 두 행렬식은 2x2입니다. 따라서 이것은 평행 사변형의 영역일 뿐입니다. 그것들을 그리고 면적을 계산해 봅시다.

첫 번째 평행사변형은 $((v)_(1))=\left(1;0 \right)$ 및 $((v)_(2))=\left(0;3 \right) 벡터를 기반으로 합니다. $:
2x2 행렬식은 평행 사변형의 면적입니다.
분명히 이것은 평행 사변형이 아니라 상당히 직사각형입니다. 그 면적은 다음과 같습니다.

두 번째 평행사변형은 $((v)_(1))=\left(1;-1 \right)$ 및 $((v)_(2))=\left(2;2 \right )$. 글쎄, 그래서 무엇? 이것은 또한 직사각형입니다:
또 다른 2x2 행렬식
이 직사각형의 변(사실, 벡터의 길이)은 피타고라스 정리를 사용하여 쉽게 계산됩니다.

\[\begin(정렬) & \left| ((v)_(1)) \right|=\sqrt(((1)^(2))+((\left(-1 \right))^(2)))=\sqrt(2); \\ & \왼쪽| ((v)_(2)) \right|=\sqrt(((2)^(2))+((2)^(2)))=\sqrt(8)=2\sqrt(2); \\ & S=\왼쪽| ((v)_(1)) \right|\cdot \left| ((v)_(2)) \right|=\sqrt(2)\cdot 2\sqrt(2)=4. \\종료(정렬)\]

마지막 행렬식을 처리해야 합니다. 이미 3x3 행렬이 있습니다. 우리는 스테레오메트리를 기억해야 합니다.

3x3 행렬식은 평행육면체의 부피입니다.
놀랍게 보이지만 실제로는 평행 육면체의 부피에 대한 공식을 기억하는 것으로 충분합니다.

여기서 $S$는 밑면의 면적(이 경우에는 $OXY$ 평면의 평행사변형 면적), $h$는 이 밑면에 그려진 높이(사실 $ z$-벡터 $((v)_(3) )$)의 좌표입니다.

평행 사변형의 면적 (별도로 그렸음)도 계산하기 쉽습니다.

\[\begin(정렬) & S=2\cdot 3=6; \\ & V=S\cdot h=6\cdot 4=24. \\종료(정렬)\]

그게 다야! 우리는 답을 적습니다.

답: 3; 4; 24.

표기법에 대한 작은 메모. 누군가는 내가 벡터 위의 "화살표"를 무시하는 것을 좋아하지 않을 것입니다. 의심되는 바에 따르면 이 방법을 사용하면 벡터를 점 또는 다른 것과 혼동할 수 있습니다.

하지만 진지하게 생각해 봅시다. 우리는 이미 성인 소년 소녀들이기 때문에 벡터에 대해 이야기할 때와 점에 대해 이야기할 때 컨텍스트에서 완벽하게 이해합니다. 화살표는 이미 수학 공식으로 가득 찬 내러티브를 어지럽힙니다.

그리고 더. 원칙적으로 1x1 행렬의 행렬식을 고려하는 데 방해가 되는 것은 없습니다. 이러한 행렬은 하나의 셀에 불과하며 이 셀에 기록된 숫자가 행렬식이 됩니다. 그러나 여기에 중요한 참고 사항이 있습니다.

고전적인 볼륨과 달리 행렬식은 우리에게 소위 " 지향적인 볼륨", 즉. 행 벡터의 고려 순서를 고려한 볼륨.

그리고 단어의 고전적인 의미에서 볼륨을 얻으려면 행렬식의 계수를 취해야 하지만 이제 그것에 대해 걱정할 필요가 없습니다. 어쨌든 몇 초 안에 행렬식을 계산하는 방법을 배울 것입니다. 모든 기호, 크기 등 :)

대수적 정의

기하학적 접근 방식의 모든 아름다움과 명확성에도 불구하고 심각한 단점이 있습니다. 바로 이 결정자를 계산하는 방법에 대해 알려주지 않습니다.

따라서 이제 우리는 대체 정의인 대수학을 분석할 것입니다. 이렇게 하려면 간단한 이론적 준비가 필요하지만 출력에서 원하는 대로 행렬의 모든 것을 계산할 수 있는 도구를 얻게 됩니다.

사실, 새로운 문제가 있을 것입니다... 하지만 먼저 해야 할 일이 있습니다.

순열 및 반전

1에서 $n$까지의 숫자를 한 줄로 작성해 보겠습니다. 당신은 다음과 같은 것을 얻습니다:

이제 (순전히 재미를 위해) 두 개의 숫자를 교환해 보겠습니다. 당신은 이웃을 변경할 수 있습니다

또는 매우 이웃하지 않을 수도 있습니다.

그리고 뭔지 알아? 하지만 아무것도 아니야! 대수학에서는 이 쓰레기를 순열이라고 합니다. 그리고 그것은 많은 속성을 가지고 있습니다.

정의. $n$ 길이의 순열은 임의의 순서로 작성된 $n$ 다른 숫자의 문자열입니다. 일반적으로 첫 번째 $n$ 자연수(즉, 숫자 1, 2, ..., $n$만)를 고려한 다음 원하는 순열을 얻기 위해 섞습니다.

순열은 벡터와 같은 방식으로 표시됩니다. 문자와 괄호 안에 해당 요소의 순차적인 열거만 있습니다. 예: $p=\left(1;3;2 \right)$ 또는 $p=\left(2;5;1;4;3 \right)$. 편지는 무엇이든 될 수 있지만 $p$로 둡니다. :)

또한 프레젠테이션의 단순성을 위해 길이 5의 순열로 작업할 것입니다. 이 순열은 이미 의심스러운 효과를 관찰할 수 있을 만큼 충분히 심각하지만 길이 6 이상의 순열만큼 취약한 뇌에는 아직 심각하지 않습니다. 다음은 이러한 순열의 예입니다.

\[\begin(정렬) & ((p)_(1))=\left(1;2;3;4;5 \right) \\ & ((p)_(2))=\left(1 ;3;2;5;4 \right) \\ & ((p)_(3))=\left(5;4;3;2;1 \right) \\\end(정렬)\]

당연히 $n$ 길이의 순열은 $\left$ 1;2;...;n \right$$ 집합에 정의되고 이 집합을 자신에 전단사적으로 매핑하는 함수로 간주될 수 있습니다. 방금 작성한 $((p)_(1))$, $((p)_(2))$ 및 $((p)_(3))$의 순열로 돌아가서 합법적으로 작성할 수 있습니다. :

\[((p)_(1))\left(1 \right)=1;((p)_(2))\left(3 \right)=2;((p)_(3))\ 왼쪽(2\오른쪽)=4;\]

길이가 $n$인 다른 순열의 수는 항상 제한되고 $n!$와 같습니다. 이것은 조합론에서 쉽게 증명할 수 있는 사실입니다. 예를 들어, 길이가 5인 모든 순열을 기록하려면 그러한 순열이 있기 때문에 많이 망설일 것입니다.

모든 순열의 주요 특성 중 하나는 그 안에 있는 역전의 수입니다.

정의. 순열 $p=\left(((a)_(1));((a)_(2));...;((a)_(n)) \right)$ — 임의의 쌍 $ \left(((a)_(i));((a)_(j)) \right)$ $i \lt j$이지만 $((a)_(i)) \gt ( (a )_(j))$. 간단히 말해서, 반전은 큰 숫자가 작은 숫자의 왼쪽에 있는 경우입니다(반드시 이웃할 필요는 없음).

$N\left(p \right)$를 사용하여 순열 $p$의 역전 수를 나타내지만 다른 교과서와 다른 저자의 다른 표기법을 충족할 수 있도록 준비해야 합니다. 여기에는 통일된 표준이 없습니다. 반전에 대한 주제는 매우 광범위하며 별도의 강의에서 이에 대해 설명합니다. 이제 우리의 임무는 실제 문제에서 계산하는 방법을 배우는 것입니다.

예를 들어, 순열 $p=\left(1;4;5;3;2 \right)$의 반전 수를 계산해 보겠습니다.

\[\left(4;3 \right);\left(4;2 \right);\left(5;3 \right);\left(5;2 \right);\left(3;2 \right ).\]

따라서 $N\left(p\right)=5$입니다. 보시다시피 여기에는 아무 문제가 없습니다. 나는 즉시 말해야 합니다. 더 나아가 우리는 $N\left(p \right)$ 숫자가 아니라 그 짝수/홀수에 관심이 있을 것입니다. 그리고 여기에서 오늘 수업의 핵심 용어로 원활하게 이동합니다.

결정 인자란 무엇인가

$A=\left[ n\times n \right]$ 를 정방 행렬이라고 합시다. 그 다음에:

정의. 행렬 $A=\left[ n\times n \right]$의 행렬식은 다음과 같이 구성된 $n!$ 항의 대수합입니다. 각 항은 $n$ 행렬 요소의 곱으로, 각 행과 각 열에서 하나씩 취해, 역전 수의 거듭제곱에 (-1)을 곱합니다.

\[\왼쪽| A \right|=\sum\limits_(n{{{\left(-1 \right)}^{N\left(p \right)}}\cdot {{a}_{1;p\left(1 \right)}}\cdot {{a}_{2;p\left(2 \right)}}\cdot ...\cdot {{a}_{n;p\left(n \right)}}}\]!}

행렬식의 각 항에 대한 요인을 선택하는 기본 사항은 동일한 행이나 동일한 열에 두 개의 요인이 없다는 사실입니다.

이 때문에 $((a)_(i;j))$ 인수의 $i$ 인덱스가 값 1, ..., $n$을 "통과"한다고 일반성을 잃지 않고 가정할 수 있습니다. , 인덱스 $j$는 첫 번째 순열입니다.

그리고 순열 $p$가 있을 때 $N\left(p\right)$의 역전을 쉽게 계산할 수 있으며 행렬식의 다음 항이 준비됩니다.

당연히, 어떤 용어로든(또는 한 번에 모두 - 사소한 일에 신경을 쓰는 이유는 무엇입니까?) 스왑 요소를 금지하는 사람은 아무도 없습니다. 그러면 첫 번째 지수도 일종의 순열을 나타냅니다. 그러나 결국에는 아무 것도 변하지 않을 것입니다. $i$ 및 $j$ 인덱스의 총 반전 수는 이러한 변태에서 패리티로 유지되며 이는 좋은 오래된 규칙과 매우 일치합니다.

요인을 재배열해도 숫자의 곱은 변하지 않습니다.

그러나 이 규칙을 행렬 곱셈에 끌어다 놓을 필요는 없습니다. 숫자의 곱셈과 달리 가환성이 아닙니다. 하지만 나는 빗나간다. :)

매트릭스 2x2

사실, 당신은 또한 1x1 행렬을 고려할 수 있습니다 - 그것은 하나의 셀이 될 것이고, 추측할 수 있듯이 그 행렬식은 이 셀에 쓰여진 숫자와 같습니다. 흥미로운 것은 없습니다.

2x2 정방 행렬을 생각해 봅시다.

\[\left[ \begin(행렬) ((a)_(11)) & ((a)_(12)) \\ ((a)_(21)) & ((a)_(22)) \\end(행렬) \right]\]

행 수가 $n=2$이므로 행렬식에는 $n!=2!=1\cdot 2=2$ 항이 포함됩니다. 다음과 같이 작성해 보겠습니다.

\[\begin(align) & ((\left(-1 \right))^(N\left(1;2 \right)))\cdot ((a)_(11))\cdot ((a) _(22))=((\left(-1 \right))^(0))\cdot ((a)_(11))\cdot ((a)_(22))=((a)_ (11))((a)_(22)); \\ & ((\left(-1 \right))^(N\left(2;1 \right)))\cdot ((a)_(12))\cdot ((a)_(21)) =((\left(-1 \right))^(1))\cdot ((a)_(12))\cdot ((a)_(21))=((a)_(12))( (a)_(21)). \\종료(정렬)\]

분명히, $N\left(1;2 \right)=0$의 두 요소로 구성된 순열 $\left(1;2 \right)$에는 반전이 없습니다. 그러나 순열 $\left(2;1 \right)$에는 하나의 반전이 있습니다(실제로는 2< 1), поэтому $N\left(2;1 \right)=1.$

전체적으로 2x2 행렬의 행렬식을 계산하는 보편적인 공식은 다음과 같습니다.

\[\왼쪽| \begin(행렬) ((a)_(11)) & ((a)_(12)) \\ ((a)_(21)) & ((a)_(22)) \\\end( 행렬) \right|=((a)_(11))((a)_(22))-((a)_(12))((a)_(21))\]

그래픽으로 이것은 주 대각선에 있는 요소의 곱에서 보조 대각선에 있는 요소의 곱을 뺀 것으로 나타낼 수 있습니다.

2x2 행렬 행렬식

몇 가지 예를 살펴보겠습니다.

\[\왼쪽| \begin(행렬) 5 & 6 \\ 8 & 9 \\end(행렬) \right|;\quad \left| \begin(행렬) 7 & 12 \\ 14 & 1 \\end(행렬) \right|.\]

해결책. 모든 것이 한 줄로 간주됩니다. 첫 번째 행렬:

그리고 두 번째:

답: -3; -161.

하지만 너무 쉬웠습니다. 3x3 행렬을 살펴보겠습니다. 이미 흥미롭습니다.

매트릭스 3x3

이제 3x3 정사각형 행렬을 고려하십시오.

\[\left[ \begin(행렬) ((a)_(11)) & ((a)_(12)) & ((a)_(13)) \\ ((a)_(21)) & ((a)_(22)) & ((a)_(23)) \\ ((a)_(31)) & ((a)_(32)) & ((a)_(33) ) \\\end(행렬) \right]\]

행렬식을 계산할 때 $3!=1\cdot 2\cdot 3=6$ 항을 얻습니다. 당황할 정도로 많지는 않지만 일부 패턴을 찾기 시작하기에 충분합니다. 먼저 세 요소의 모든 순열을 작성하고 각각의 역전을 계산해 보겠습니다.

\[\begin(align) & ((p)_(1))=\left(1;2;3 \right)\Rightarrow N\left(((p)_(1)) \right)=N\ 왼쪽(1;2;3\오른쪽)=0; \\ & ((p)_(2))=\left(1;3;2 \right)\오른쪽 화살표 N\left(((p)_(2)) \right)=N\left(1;3 ;2\오른쪽)=1; \\ & ((p)_(3))=\left(2;1;3 \right)\오른쪽 화살표 N\left(((p)_(3)) \right)=N\left(2;1 ;3\오른쪽)=1; \\ & ((p)_(4))=\left(2;3;1 \right)\오른쪽 화살표 N\left(((p)_(4)) \right)=N\left(2;3 ;1\오른쪽)=2; \\ & ((p)_(5))=\left(3;1;2 \right)\Rightarrow N\left(((p)_(5)) \right)=N\left(3;1 ;2\오른쪽)=2; \\ & ((p)_(6))=\left(3;2;1 \right)\오른쪽 화살표 N\left(((p)_(6)) \right)=N\left(3;2 ;1\오른쪽)=3. \\종료(정렬)\]

예상대로 $((p)_(1))$, ... $((p)_(6))$ 총 6개의 순열이 있습니다(물론 다른 순서로 쓸 수 있습니다. 변경되지 않음), 반전 수는 0에서 3까지 다양합니다.

일반적으로 세 개의 더하기 항($N\left(p \right)$이 짝수인 경우)과 세 개의 빼기 항이 있습니다. 일반적으로 행렬식은 다음 공식에 따라 계산됩니다.

\[\왼쪽| \begin(행렬) ((a)_(11)) & ((a)_(12)) & ((a)_(13)) \\ ((a)_(21)) & ((a) _(22)) & ((a)_(23)) \\ ((a)_(31)) & ((a)_(32)) & ((a)_(33)) \\\end (행렬) \right|=\begin(행렬) ((a)_(11))((a)_(22))((a)_(33))+((a)_(12))( (a)_(23))((a)_(31))+((a)_(13))((a)_(21))((a)_(32))- \\ -( (a)_(13))((a)_(22))((a)_(31))-((a)_(12))((a)_(21))((a)_ (33))-((a)_(11))((a)_(23))((a)_(32)) \\\end(행렬)\]

지금 앉아서 이 모든 지수를 맹렬히 몰아붙이지 마십시오! 이해할 수 없는 숫자 대신 다음 니모닉 규칙을 기억하는 것이 좋습니다.

삼각형 규칙. 3x3 행렬의 행렬식을 찾으려면 주 대각선과 이 대각선에 평행한 변이 있는 이등변 삼각형의 꼭짓점에서 요소의 세 곱을 더한 다음 동일한 세 곱을 빼야 합니다. . 도식적으로 다음과 같습니다.

3x3 행렬 행렬식: 삼각형의 규칙

그들이 대수학에 관한 모든 종류의 교과서와 매뉴얼에서 그리는 것을 좋아하는 것은 이 삼각형(또는 원하는 대로 오각형)입니다. 그러나 슬픈 이야기는 하지 맙시다. 실제 주석 전에 워밍업하기 위해 그러한 결정 요인 중 하나를 더 잘 계산해 봅시다. :)

일. 행렬식 계산:

\[\왼쪽| \begin(행렬) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 1 \\end(행렬) \right|\]

해결책. 우리는 삼각형의 법칙에 따라 일합니다. 먼저 주대각선과 평행한 요소로 구성된 세 가지 항을 계산해 보겠습니다.

\[\begin(정렬) & 1\cdot 5\cdot 1+2\cdot 6\cdot 7+3\cdot 4\cdot 8= \\ & =5+84+96=185 \\end(정렬) \]

이제 측면 대각선을 처리해 보겠습니다.

\[\begin(정렬) & 3\cdot 5\cdot 7+2\cdot 4\cdot 1+1\cdot 6\cdot 8= \\ & =105+8+48=161 \\end(정렬) \]

첫 번째 숫자에서 두 번째 숫자를 빼는 것만 남아 있으며 답을 얻습니다.

그게 다야!

그러나 3x3 행렬의 결정 요인은 아직 기술의 정점이 아닙니다. 가장 흥미로운 것은 우리를 더 기다리고 있습니다. :)

행렬식 계산을 위한 일반 체계

우리가 알다시피 행렬 $n$의 차원이 증가함에 따라 행렬식의 항의 수는 $n!$이고 빠르게 증가합니다. 결국 factorial은 매우 빠르게 성장하는 함수입니다.

이미 4x4 행렬의 경우 (즉, 순열을 통해) 행렬식을 미리 계산하는 것은 좋지 않습니다. 나는 일반적으로 5x5 이상에 대해 조용합니다. 따라서 행렬식의 일부 속성은 경우와 연결되지만 이를 이해하기 위해서는 약간의 이론적 준비가 필요합니다.

준비가 된? 가다!

매트릭스 마이너 란 무엇입니까

임의의 행렬 $A=\left[ m\times n \right]$가 주어집니다. 참고: 반드시 정사각형일 필요는 없습니다. 행렬식과 달리 미성년자는 가혹한 정사각형 행렬에만 존재하는 것이 아니라 귀여운 것입니다. 이 행렬에서 $1\le k\le m$ 및 $1\le k\le n$를 사용하여 여러 행과 열(예: $k$)을 선택합니다. 그 다음에:

정의. $k$ 차수 소수는 선택한 $k$ 열과 행의 교차점에 나타나는 정방 행렬의 행렬식입니다. 우리는 또한 이 새로운 매트릭스 자체를 마이너라고 부를 것입니다.

이러한 미성년자는 $((M)_(k))$로 표시됩니다. 당연히, 하나의 행렬은 $k$ 차수의 전체 무리를 가질 수 있습니다. 다음은 $\left[ 5\times 6 \right]$ 행렬에 대한 2차 단조의 예입니다.
$k = 2$ 열과 행을 선택하여 마이너 구성

위의 예와 같이 선택한 행과 열을 나란히 배치할 필요는 없습니다. 가장 중요한 것은 선택한 행과 열의 수가 동일하다는 것입니다(이것은 $k$입니다).

또 다른 정의가 있습니다. 아마도 누군가가 더 좋아할 것입니다:

정의. 직사각형 행렬 $A=\left[ m\times n \right]$가 주어집니다. 하나 이상의 열과 하나 이상의 행을 삭제한 후 $\left[ k\times k \right]$ 크기의 정방 행렬이 형성되면 행렬의 행렬식은 소수 $((M)_(k) )$ . 우리는 또한 때때로 행렬 자체를 마이너라고 부를 것입니다. 이것은 컨텍스트에서 명확할 것입니다.

내 고양이가 말했듯이 때로는 발코니에 앉아 야옹하는 것보다 11 층에서 한 번 음식을 얻는 것이 좋습니다.

예시. 매트릭스를 보자

행 1과 열 2를 선택하면 1차 마이너를 얻습니다.

\[((M)_(1))=\왼쪽| 7\오른쪽|=7\]

행 2, 3 및 열 3, 4를 선택하면 2차 미성년자를 얻습니다.

\[((M)_(2))=\왼쪽| \begin(행렬) 5 & 3 \\ 6 & 1 \\\end(행렬) \right|=5-18=-13\]

세 개의 행과 열 1, 2, 4를 모두 선택하면 세 번째 순서의 마이너가 있습니다.

\[((M)_(3))=\왼쪽| \begin(행렬) 1 & 7 & 0 \\ 2 & 4 & 3 \\ 3 & 0 & 1 \\end(행렬) \right|\]

독자가 1, 2, 3차의 다른 미성년자를 찾는 것은 어렵지 않을 것입니다. 따라서 우리는 계속 진행합니다.

대수적 덧셈

"글쎄요, 그리고 이 미니언들이 우리에게 미성년자에게 주는 것은 무엇인가요?" 당신은 반드시 물어볼 것입니다. 그들 스스로, 아무것도. 그러나 정사각형 행렬에서 각 미성년자는 "동반자"를 갖습니다. 추가 미성년자 및 대수 추가. 그리고 이 두 개의 slapsticks를 함께 사용하면 견과류와 같은 행렬식을 클릭할 수 있습니다.

정의. 정방 행렬 $A=\left[ n\times n \right]$가 주어지고 여기서 소수 $((M)_(k))$가 선택됩니다. 그런 다음 보조 $((M)_(k))$에 대한 추가 보조는 원래 행렬 $A$의 일부이며 보조 $((M)의 컴파일과 관련된 모든 행과 열을 삭제한 후에도 남아 있습니다. )_(k))$:
미성년자에 대한 추가 미성년자 $((M)_(2))$
한 가지 요점을 명확히 합시다. 추가 단조는 "매트릭스의 일부"가 아니라 이 곡의 결정 요소입니다.

추가 미성년자는 별표로 표시됩니다. $M_(k)^(*)$:

여기서 $A\nabla ((M)_(k))$ 작업은 문자 그대로 "$((M)_(k))$에 포함된 행과 열을 $A$에서 삭제"를 의미합니다. 이 연산은 일반적으로 수학에서 받아들여지지 않습니다 - 저는 단지 이야기의 아름다움을 위해 스스로 생각해 냈습니다. :)

보완 미성년자는 단독으로 거의 사용되지 않습니다. 그것들은 더 복잡한 구조의 일부인 대수적 덧셈입니다.

정의. 마이너 $((M)_(k))$의 대수 보수는 $((\left(-1 \right))^(S))를 곱한 보수 마이너 $M_(k)^(*)$입니다. $ , 여기서 $S$는 원래 보조 $((M)_(k))$에 관련된 모든 행과 열의 수를 합한 것입니다.

일반적으로 보조 $((M)_(k))$의 대수 보수는 $((A)_(k))$로 표시됩니다. 그래서:

\[((A)_(k))=((\left(-1 \right))^(S))\cdot M_(k)^(*)\]

딱딱한? 언뜻보기에 그렇습니다. 그러나 그것은 정확하지 않습니다. 정말 쉽기 때문입니다. 다음 예를 고려하십시오.

예시. 주어진 4x4 행렬:

우리는 두 번째 주문의 미성년자를 선택합니다.

\[((M)_(2))=\왼쪽| \begin(행렬) 3 & 4 \\ 15 & 16 \\end(행렬) \right|\]

Captain Evidence는 말 그대로 1행과 4열, 3열과 4열이 이 미성년자의 편집에 관여했음을 암시합니다.

숫자 $S$를 찾고 대수적 보수를 구해야 합니다. 관련된 행(1 및 4)과 열(3 및 4)의 수를 알고 있으므로 모든 것이 간단합니다.

\[\begin(정렬) & S=1+4+3+4=12; \\ & ((A)_(2))=((\left(-1 \right))^(S))\cdot M_(2)^(*)=((\left(-1 \right) )^(12))\cdot \left(-4 \right)=-4\end(align)\]

답: $((A)_(2))=-4$

그게 다야! 사실, 추가 부전공과 대수 덧셈의 전체적인 차이는 앞에 있는 빼기에만 있고, 그 후에도 항상 그런 것은 아닙니다.

라플라스의 정리

그래서 우리는 사실 이 모든 부전공과 대수적 덧셈이 필요한 이유에 도달했습니다.

행렬식의 분해에 대한 라플라스의 정리. $k$ 행(열)이 $1\le k\le n-1$인 $\left[ n\times n \right]$ 크기의 행렬에서 선택되도록 합니다. 그런 다음이 행렬의 행렬식은 선택한 행(열)과 대수적 보수에 포함된 $k$ 차수의 모든 곱의 합과 같습니다.

\[\왼쪽| A \right|=\sum(((M)_(k))\cdot ((A)_(k)))\]

게다가, 정확히 $C_(n)^(k)$ 그러한 용어가 있을 것입니다.

좋아요, 좋아요: $C_(n)^(k)$에 대해 - 이미 과시하고 있습니다. 원래의 라플라스 정리에는 그런 것이 없었습니다. 그러나 아무도 조합론을 취소하지 않았으며, 말 그대로 조건을 얼핏 보면 정확히 그 만큼 많은 항이 있을 것임을 스스로 확인할 수 있습니다. :)

이것이 특별히 어렵지는 않지만 우리는 그것을 증명하지 않을 것입니다. 모든 계산은 좋은 오래된 순열과 짝수/홀수 역전으로 귀결됩니다. 그러나 증거는 별도의 단락에서 제시될 것이며 오늘 우리는 순전히 실용적인 교훈을 얻습니다.

따라서 미성년자가 행렬의 별도 셀인 경우 이 정리의 특별한 경우로 전환합니다.

행렬식의 행 및 열 확장

우리가 지금 이야기하려는 것은 순열, 미성년자 및 대수 추가가 포함된 이 모든 게임이 시작된 행렬식 작업을 위한 주요 도구입니다.

읽고 즐기십시오:

라플라스 정리(행/열의 행렬식 분해)의 결과입니다. $\left[ n\times n \right]$ 행렬에서 한 행을 선택합니다. 이 행의 미성년자는 $n$ 개별 셀입니다.

\[((M)_(1))=((a)_(ij)),\quad j=1,...,n\]

추가 미성년자도 쉽게 계산할 수 있습니다. 원래 행렬을 가져와서 $((a)_(ij))$가 포함된 행과 열에 줄을 긋기만 하면 됩니다. 이러한 미성년자를 $M_(ij)^(*)$라고 합니다.

대수적 보수의 경우 숫자 $S$도 필요하지만 1차 부전공의 경우 $((a)_(ij))$ 셀의 "좌표"의 합계입니다.

그리고 나서 원래 행렬식은 Laplace의 정리에 따라 $((a)_(ij))$ 및 $M_(ij)^(*)$로 작성할 수 있습니다.

\[\왼쪽| A \right|=\sum\limits_(j=1)^(n)(((a)_(ij))\cdot ((\left(-1 \right))^(i+j))\cdot ((M)_(ij)))\]

그게 다야 행 확장 공식. 그러나 열의 경우에도 마찬가지입니다.

이 결론에서 몇 가지 결론을 도출할 수 있습니다.

이 구성표는 행과 열 모두에 대해 똑같이 잘 작동합니다. 실제로 대부분의 경우 분해는 선이 아니라 열을 따라 정확하게 진행됩니다.
확장의 항 수는 항상 정확히 $n$입니다. 이것은 $C_(n)^(k)$보다 훨씬 적고 $n!$보다 훨씬 적습니다.
단일 행렬식 $\left[ n\times n \right]$ 대신에, $\left[ \left(n-1 \right)\times \left(n- 1 \오른쪽) \오른쪽 ]$.

마지막 사실이 특히 중요합니다. 예를 들어, 잔인한 4x4 행렬식 대신 이제 여러 3x3 행렬식을 계산하는 것으로 충분합니다. 어떻게든 처리할 것입니다. :)

일. 행렬식 찾기:

\[\왼쪽| \begin(행렬) 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\end(행렬) \right|\]

해결책. 이 행렬식을 첫 번째 줄로 확장해 보겠습니다.

\[\시작(정렬)\왼쪽| A \right|=1\cdot ((\left(-1 \right))^(1+1))\cdot \left| \begin(행렬) 5 & 6 \\ 8 & 9 \\\end(행렬) \right|+ & \\ 2\cdot ((\left(-1 \right))^(1+2))\cdot \왼쪽| \begin(행렬) 4 & 6 \\ 7 & 9 \\\end(행렬) \right|+ & \\ 3\cdot ((\left(-1 \right))^(1+3))\cdot \왼쪽| \begin(행렬) 4 & 5 \\ 7 & 8 \\end(행렬) \right|= & \\\end(정렬)\]

\[\begin(align) & =1\cdot \left(45-48 \right)-2\cdot \left(36-42 \right)+3\cdot \left(32-35 \right)= \\ & =1\cdot \left(-3 \right)-2\cdot \left(-6 \right)+3\cdot \left(-3 \right)=0. \\종료(정렬)\]

일. 행렬식 찾기:

\[\왼쪽| \begin(행렬) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\end(행렬) \right|\ ]

해결책. 변경을 위해 이번에는 열로 작업해 보겠습니다. 예를 들어, 마지막 열에는 한 번에 두 개의 0이 있습니다. 분명히 이것은 계산을 크게 줄입니다. 이제 그 이유를 알게 될 것입니다.

따라서 네 번째 열의 행렬식을 확장합니다.

\[\시작(정렬)\왼쪽| \begin(행렬) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\end(행렬) \right|= 0\cdot ((\left(-1 \right))^(1+4))\cdot \left| \begin(행렬) 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end(행렬) \right|+ & \\ +1\cdot ((\left(-1 \ 오른쪽))^(2+4))\cdot \left| \begin(행렬) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end(행렬) \right|+ & \\ +1\cdot ((\left(-1 \ 오른쪽))^(3+4))\cdot \left| \begin(행렬) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end(행렬) \right|+ & \\ +0\cdot ((\left(-1 \ 오른쪽))^(4+4))\cdot \left| \begin(행렬) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\end(행렬) \right| &\\\\종료(정렬)\]

그리고 나서 - 오, 기적! - 승수가 "0"이기 때문에 두 항은 즉시 배수구 아래로 날아갑니다. 우리가 쉽게 다룰 수 있는 2개의 3x3 행렬식이 더 있습니다.

\[\begin(정렬) & \left| \begin(행렬) 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\end(행렬) \right|=0+0+1-1-1-0=-1; \\ & \왼쪽| \begin(행렬) 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end(행렬) \right|=0+1+1-0-0-1=1. \\종료(정렬)\]

우리는 소스로 돌아가서 답을 찾습니다.

\[\왼쪽| \begin(행렬) 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\end(행렬) \right|= 1\cdot \left(-1 \right)+\left(-1 \right)\cdot 1=-2\]

자, 이제 끝났습니다. 그리고 아니 4! = 24개의 용어는 계산할 필요가 없었습니다. :)

답: -2

행렬식의 기본 속성

마지막 문제에서 행렬의 행(열)에 0이 있으면 행렬식의 확장과 일반적으로 모든 계산이 어떻게 크게 간소화되는지 확인했습니다. 자연스러운 질문이 생깁니다. 이러한 0이 원래 존재하지 않은 행렬에서도 이러한 0이 나타나게 할 수 있습니까?

대답은 명확합니다. ~ 할 수있다. 여기에서 행렬식의 속성이 도움이 됩니다.

두 개의 행(열)을 제자리에서 바꾸면 행렬식이 변경되지 않습니다.
하나의 행(열)에 숫자 $k$를 곱하면 전체 행렬식에도 $k$가 곱해집니다.
한 문자열을 가져 와서 다른 문자열에서 몇 번이든 더(빼기)하면 행렬식이 변경되지 않습니다.
행렬식의 두 행이 같거나 비례하거나 행 중 하나가 0으로 채워지면 전체 행렬식이 0입니다.
위의 모든 속성은 열에도 적용됩니다.
행렬을 전치해도 행렬식은 변경되지 않습니다.
행렬 곱의 행렬식은 행렬식의 곱과 같습니다.

특히 가치가 있는 것은 세 번째 속성입니다. 올바른 위치에 0이 나타날 때까지 한 행(열)에서 다른 행(열)을 뺍니다..

대부분의 경우 계산은 한 요소를 제외한 모든 열에서 전체 열을 "제로화"한 다음 이 열을 따라 행렬식을 확장하여 크기가 1보다 작은 행렬을 얻습니다.

이것이 실제로 어떻게 작동하는지 봅시다.

일. 행렬식 찾기:

\[\왼쪽| \begin(행렬) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\end(행렬) \right|\ ]

해결책. 여기의 0은 그대로 관찰되지 않으므로 모든 행이나 열에서 "빈" 수 있습니다. 계산량은 거의 동일합니다. 사소한 일을하지 않고 첫 번째 열을 "0으로"하지 마십시오. 이미 단위가있는 셀이 있으므로 첫 번째 줄을 가져 와서 두 번째 줄에서 4 번, 세 번째 줄에서 3 번, 마지막 줄에서 2 번 빼십시오.

결과적으로 새로운 행렬을 얻을 수 있지만 행렬식은 동일합니다.

\[\begin(행렬)\left| \begin(행렬) 1 & 2 & 3 & 4 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ 2 & 3 & 4 & 1 \\end(행렬) \right|\ 시작(행렬) \아래쪽 화살표 \\ -4 \\ -3 \\ -2 \\end(행렬)= \\ =\왼쪽| \begin(행렬) 1 & 2 & 3 & 4 \\ 4-4\cdot 1 & 1-4\cdot 2 & 2-4\cdot 3 & 3-4\cdot 4 \\ 3-3\cdot 1 & 4-3\cdot 2 & 1-3\cdot 3 & 2-3\cdot 4 \\ 2-2\cdot 1 & 3-2\cdot 2 & 4-2\cdot 3 & 1-2\cdot 4 \ \\end(행렬) \right|= \\ =\left| \begin(행렬) 1 & 2 & 3 & 4 \\ 0 & -7 & -10 & -13 \\ 0 & -2 & -8 & -10 \\ 0 & -1 & -2 & -7 \\ \end(행렬)\right| \\끝(행렬)\]

이제 Piglet의 평정성을 사용하여 첫 번째 열에서 이 행렬식을 분해합니다.

\[\begin(행렬) 1\cdot ((\left(-1 \right))^(1+1))\cdot \left| \begin(행렬) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\end(행렬) \right|+0\cdot ((\ 왼쪽(-1 \오른쪽))^(2+1))\cdot \left| ... \right|+ \\ +0\cdot ((\left(-1 \right))^(3+1))\cdot \left| ... \right|+0\cdot ((\left(-1 \right))^(4+1))\cdot \left| ... \오른쪽| \\끝(행렬)\]

첫 번째 항만 "생존"할 것이 분명합니다. 나머지에서는 행렬식이 여전히 0으로 곱해지기 때문에 행렬식을 쓰지도 않았습니다. 행렬식 앞의 계수는 1과 같습니다. 기록되지 않을 수 있습니다.

그러나 행렬식의 세 줄 모두에서 "빼기"를 제거할 수 있습니다. 사실, 우리는 인자(−1)를 세 번 제거했습니다:

\[\왼쪽| \begin(행렬) -7 & -10 & -13 \\ -2 & -8 & -10 \\ -1 & -2 & -7 \\\end(행렬) \right|=\cdot \left| \begin(행렬) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\end(행렬) \right|\]

우리는 삼각형의 규칙에 따라 이미 계산할 수 있는 작은 행렬식 3x3을 얻었습니다. 그러나 우리는 첫 번째 열에서 그것을 분해하려고 노력할 것입니다. 마지막 줄의 이점은 자랑스럽게 하나입니다.

\[\begin(정렬) & \left(-1 \right)\cdot \left| \begin(행렬) 7 & 10 & 13 \\ 2 & 8 & 10 \\ 1 & 2 & 7 \\end(행렬) \right|\begin(행렬) -7 \\ -2 \\ \위 화살표 \ \\end(행렬)=\left(-1 \right)\cdot \left| \begin(행렬) 0 & -4 & -36 \\ 0 & 4 & -4 \\ 1 & 2 & 7 \\end(행렬) \right|= \\ & =\cdot \left| \begin(행렬) -4 & -36 \\ 4 & -4 \\end(행렬) \right|=\left(-1 \right)\cdot \left| \begin(행렬) -4 & -36 \\ 4 & -4 \\end(행렬) \right| \\종료(정렬)\]

물론 여전히 재미를 가지고 행(열)의 2x2 행렬을 분해할 수 있지만 우리는 당신에게 충분하므로 답을 계산합니다.

\[\left(-1 \right)\cdot \left| \begin(행렬) -4 & -36 \\ 4 & -4 \\\end(행렬) \right|=\left(-1 \right)\cdot \left(16+144 \right)=-160\ ]

꿈은 이렇게 깨집니다. 대답에는 -160 만 있습니다. :)

답: -160.

마지막 작업으로 넘어가기 전에 몇 가지 참고 사항:

원래 행렬은 2차 대각선에 대해 대칭이었습니다. 분해의 모든 마이너는 동일한 2차 대각선에 대해서도 대칭입니다.
엄밀히 말하면, 우리는 아무 것도 배치할 수 없었고 주 대각선 아래에 솔리드 0이 있을 때 행렬을 상부 삼각 형태로 가져왔습니다. 그러면 (기하학적 해석에 따라) 행렬식은 주대각선의 숫자인 $((a)_(ii))$의 곱과 같습니다.

일. 행렬식 찾기:

\[\왼쪽| \begin(행렬) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\end(행렬) \right|\ ]

해결책. 음, 여기 첫 번째 줄은 "제로화"를 요구합니다. 첫 번째 열을 취하고 다른 모든 열에서 정확히 한 번 뺍니다.

\[\begin(정렬) & \left| \begin(행렬) 1 & 1 & 1 & 1 \\ 2 & 4 & 8 & 16 \\ 3 & 9 & 27 & 81 \\ 5 & 25 & 125 & 625 \\end(행렬) \right|= \\&=\왼쪽| \begin(행렬) 1 & 1-1 & 1-1 & 1-1 \\ 2 & 4-2 & 8-2 & 16-2 \\ 3 & 9-3 & 27-3 & 81-3 \\ 5 & 25-5 & 125-5 & 625-5 \\\end(행렬) \right|= \\ & =\left| \begin(행렬) 1 & 0 & 0 & 0 \\ 2 & 2 & 6 & 14 \\ 3 & 6 & 24 & 78 \\ 5 & 20 & 120 & 620 \\end(행렬) \right| \\종료(정렬)\]

첫 번째 행을 확장한 다음 나머지 행에서 공통 요소를 제거합니다.

\[\cdot\left| \begin(행렬) 2 & 6 & 14 \\ 6 & 24 & 78 \\ 20 & 120 & 620 \\\end(행렬) \right|=\cdot \left| \begin(행렬) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\end(행렬) \right|\]

다시 우리는 "아름다운"숫자를 관찰하지만 이미 첫 번째 열에 있습니다. 우리는 그것에 따라 행렬식을 분해합니다.

\[\begin(정렬) & 240\cdot \left| \begin(행렬) 1 & 3 & 7 \\ 1 & 4 & 13 \\ 1 & 6 & 31 \\end(행렬) \right|\begin(행렬) \downarrow \\ -1 \\ -1 \ \\end(행렬)=240\cdot \left| \begin(행렬) 1 & 3 & 7 \\ 0 & 1 & 6 \\ 0 & 3 & 24 \\\end(행렬) \right|= \\ & =240\cdot ((\left(-1 \ 오른쪽))^(1+1))\cdot \left| \begin(행렬) 1 & 6 \\ 3 & 24 \\end(행렬) \right|= \\ & =240\cdot 1\cdot \left(24-18 \right)=1440 \\end( 맞추다)\]

주문하다. 문제 해결됨.

답: 1440

1. 표지판의 일반적인 규칙. 미래에는 두 개의 숫자 순열이 있는 행렬식에 해당 용어가 어떤 기호로 들어가는지 알아내는 것이 유용할 것입니다.

알아내기 위해서는 요인들을 선의 순서대로 배열해야 합니다. 두 요소가 교환되면 첫 번째 지수와 두 번째 지수 모두에서 전치가 발생하므로 첫 번째 지수의 역전 수와 두 번째 지수의 역전 수가 홀수로 변경되므로 합이 다음과 같이 변경됩니다. 짝수. 따라서 두 요인의 위치가 변경되어도 결과적으로 요인의 순서가 변경되어도 변경되지 않습니다. 왜냐하면 순서의 모든 변경은 여러 쌍의 위치 변경과 동일하기 때문입니다. 따라서 항이 행렬식에 들어가는 부호는 입니다. 실제로, 요소를 행 순서로 가져온 후 열 번호의 시퀀스라고 하면 다음이 됩니다.

그리고 이것은 우리에게 관심있는 기간이 행렬식에 포함되는 요인 ±1입니다.

2. 전치 행렬의 행렬식은 원래 행렬과 같습니다. 즉, 행렬이 전치될 때 행렬식이 변하지 않습니다.

실제로, 원래 행렬의 각 행과 각 열에서 하나씩 요소의 곱을 취하는 것은 전치 행렬에 대해 이것을 수행하는 것과 동일합니다. 또한, 원본의 행 번호는 전치된 열 번호이고, 원본의 열 번호는 전치된 것의 행 번호입니다. 따라서 각 항은 원래 행렬의 행렬식과 동일한 인수로 전치된 행렬의 행렬식에 포함됩니다.

두 속성 집합은 한정자에서 행과 열이 완전히 동일함을 나타냅니다. 따라서 행에 대해 설정된 모든 추가 속성은 열에 대해 유효한 상태로 유지됩니다.

다음 두 속성은 행렬식이 행의 요소에 대해 선형임을 의미합니다.

3. 어떤 행의 요소가 두 항의 합으로 표시되면 행렬식은 두 행렬식의 합과 같으며 첫 번째에서 표시된 행의 요소는 첫 번째 항과 같으며 두 번째 항에서는 - 두 번째로.

이 속성은 구두 공식에서 공식으로 이동하면 더 투명해집니다.